基于多元表征理論下的數(shù)學教學實踐與思考

江蘇省常熟理工學院 (215500)

盛一凡*

江蘇省常熟市滸浦高級中學 (215512)

殷偉康

基于多元表征理論下的數(shù)學教學實踐與思考

江蘇省常熟理工學院 (215500)

盛一凡*

江蘇省常熟市滸浦高級中學 (215512)

殷偉康

所謂“多元表征理論”即是更加強調數(shù)學問題心理表征的多元性，強調數(shù)學問題表征不同方面的相互滲透與必要互補.更為重要的是，“多元表征理論”突出強調了數(shù)學問題的心理表征往往包含多個不同的方面或成分，這些成分對于數(shù)學問題的正確理解都具有重要的作用；另外，與片面強調其中的某一成分相對應，我們又應更加重視這些成分之間的聯(lián)結與相互轉換，進行多元表征，發(fā)現(xiàn)解題思路，有助于學生不斷完善認知結構，更有利于培養(yǎng)學生的數(shù)學表達能力，提升數(shù)學素養(yǎng).

1.加強數(shù)學問題表征的轉換訓練，提高數(shù)學表達能力

著名心理學家西蒙指出：“表征是問題解決的一個中心環(huán)節(jié)，它說明問題在頭腦里是如何呈現(xiàn)的，如何表現(xiàn)出來的.”因而，在數(shù)學概念和數(shù)學公式的教學過程中要注重引導學生把握表征取向，加強數(shù)學問題表征的轉換訓練，創(chuàng)設問題情境，使問題表征盡可能和數(shù)學概念、數(shù)學公式相匹配，加深對概念、公式的理解.

基本不等式不同于方程、函數(shù)這樣的以等式變換為主要特征的數(shù)學內涵，出現(xiàn)了一種更加靈活的數(shù)學現(xiàn)象：研究兩個變量組成的代數(shù)式之間的不等關系.兩個變量，兩個代數(shù)式，一個恒成立的不等關系式.這種新型的數(shù)學模式對學生來說是陌生的，不少學生的思維可能仍然囿于原有的思維模式之中，此時需要教師有意識地指導學生進行問題表征轉換訓練，展示其不同的表征形式，讓學生了解數(shù)學問題表征的特點和主要表征形式，并逐步掌握問題表征的基本要領，促進學生建立數(shù)學公式的多元表征和深層次理解基本不等式.

(1)語言表征：兩個正數(shù)的等差中項不小于它們的等比中項.也可表述為兩個正數(shù)的算術平均數(shù)不小于它們的幾何平均數(shù)(當且僅當兩個正數(shù)相等時，這兩種平均數(shù)相等).讓學生通過用簡潔準確的語言表述公式，這不僅有助于學生理解基本不等式，而且有利于提高學生運用數(shù)學語言表達交流能力和數(shù)學素養(yǎng).

(3)操作表征：利用Excel 進行現(xiàn)場操作，讓學生分別取值計算兩個正數(shù)的等差中項、等比中項，通過對比計算結果，發(fā)現(xiàn)兩個代數(shù)式之間的關系，由此猜想出基本不等式.這樣有利于學生進行歸納、概括與猜想活動，提供具體和易于理解的直接經(jīng)驗.

“商品打折”問題的設計，把生活中的鮮活題材引入課堂教學，賦予“基本不等式”以新的活力，讓學生從數(shù)學角度觀察日常生活中的現(xiàn)象，經(jīng)歷抽象提煉數(shù)學模型和數(shù)學應用的過程，培養(yǎng)學生數(shù)學素養(yǎng).

圖1

試指出圖中哪條線段分別是a,b算術平均值和幾何平均值？能否比較他們的大小關系？

借助學生熟知的幾何圖形，引導學生從幾何圖形中抽象出基本不等式，使學生體會數(shù)形結合的思想，領悟數(shù)學韻味，同時也使得學生理解很多看似抽象的代數(shù)不等式都源于幾何圖形，體會從形到數(shù)的轉化.

通過數(shù)學問題表征的轉換訓練，幫助學生建立起各種表征方式之間的聯(lián)系，不僅可以不斷提升學生對數(shù)學問題的各種表征進行系統(tǒng)內轉換和系統(tǒng)間的轉譯能力，提高多元表征能力，而且還能使學生對數(shù)學問題的表征形成直覺和積累經(jīng)驗，從而加深對問題的理解和數(shù)學表征的體驗，領悟其本質，提高數(shù)學表達能力.

2.創(chuàng)設問題多維表征的交流平臺，提高問題表征能力

數(shù)學問題的表征模式是由數(shù)學概念、命題、算法與策略經(jīng)驗等基本模式產(chǎn)生的心理圖式.數(shù)學概念、命題、算法等基本模式具有對數(shù)學問題轉譯方式的多樣性，從而形成了表征方式的多樣性，每一種表征中的聯(lián)結詞都包含著解題策略和方法.問題多維表征是解題思路產(chǎn)生的源泉，因而在數(shù)學教學過程中，教師要善于運用啟發(fā)性提示語：“你能否根據(jù)自己的聯(lián)想，嘗試用適當?shù)姆绞綄栴}進行重新表征？”“在遇到困難的情況下，你能否變換問題的表征方式，調整解題的思維方向？”激活學生原有的知識塊，產(chǎn)生聯(lián)想，誘發(fā)學生進行多維表征.

問題2(2015年江蘇省高考試題第10題)在平面直角坐標系xOy中，以點(1，0)為圓心且與直線mx-y-2m-1=0(m∈R)相切的所有圓中，半徑最大的圓的標準方程為________.

表征2：(函數(shù)模式)令m+1=t，則t≠0，

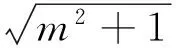
通過不同表征方式的交流，處于不同層次的學生將會對自己的表征方式進行同化和順應，將會改進、完善已有信息表征方式，提升問題表征的質量，積累問題表征的經(jīng)驗.

3.通過問題表征系統(tǒng)的建構與分析，形成解題思維走向

當數(shù)學問題中信息較多時，則容易產(chǎn)生干擾交錯的現(xiàn)象，很多學生常常因此出現(xiàn)思維不暢，無法順利解答.通過建構表征系統(tǒng)，可以理順信息間的邏輯關系和因果聯(lián)系，進而幫助學生形成清晰的解題思維走向.

問題3(2016年江蘇省高考試題第14題)在銳角三角形ABC中，sinA=2sinBsinC，則tanAtanBtanC的最小值是________.

通過建構表征系統(tǒng)，本題信息：①銳角三角形ABC；②sinA=2sinBsinC；③tanAtanBtanC的最小值.引導學生從中提取出核心信息“sinA=2sinBsinC”，據(jù)此聚攏所有信息，逐步把握問題的本質，最終形成條件與目標之間的思維通道.

tanAtanBtanC的最小值是8.

思維走向2：(以地位關系為起點)將核心信息②化解為tanB+tanC=2tanBtanC，據(jù)此，聯(lián)想三角形中重要結論tanA+tanB+tanC=tanAtanBtanC，從整體思考，運用基本不等式即可.由信息①得tanA>0,tanB>0，tanC>0，tanAtanBtanC=tanA+tanB+tanC=tanA+2tanBtanC

通過建構表征系統(tǒng)，確定核心信息，理順信息之間的關系，按照不同的起點形成相應的思維走向.

4.學會選擇合理的模式表征的方法，簡約解題思維過程

數(shù)學問題的解決的前提條件是對問題進行合理表征.辨別問題的類型，根據(jù)問題的結構特征，聯(lián)想已有的模式結構特征，進行模式識別(包括模式特征、適用條件、模式的本質和功能)，再進行問題表征.問題表征是否適宜，直接影響到數(shù)學問題解決的難易和快慢.

適當?shù)膱D形表征有助于問題的形象直觀思考，引導學生對問題深層次結構特征的正確表征，更容易激活問題圖式，從而順利解決問題.合理的模式表征有助于簡約問題解決的思維長度，快速解決問題.

總之，在教學中要創(chuàng)設展示學生問題表征的時機，引導學生深入問題內部，建構恰當?shù)男畔⒈碚飨到y(tǒng)和高質量的盡可能多的圖式表征，讓學生積累豐富的問題表征的方式和經(jīng)驗，有效地提高學生理解問題和問題表征能力.

[1]殷偉康.培養(yǎng)學生數(shù)學問題表征能力 “三部曲”[J].中學數(shù)學(高中版),2013(7)：65-67.

[2]陳勇,丁益民.解題活動中表征系統(tǒng)的建構與分析[J].中學數(shù)學(高中版),2015(1)：23-24.

[3]陸學政.“多元表征理論”指導下的“數(shù)列概念”教學[J].中學數(shù)學教學參考,2012(4)：10-13.

[4]王思儉.2015年高考數(shù)學江蘇卷特點回眸[J].中小學數(shù)學(高中版),2015(7-8)：119-122.

* 作者為2015級經(jīng)濟統(tǒng)計學專業(yè)在讀生.