多視角寬思維妙解函數零點問題

江蘇省連云港市錦屏高級中學 (222021)

車樹勤

多視角寬思維妙解函數零點問題

江蘇省連云港市錦屏高級中學 (222021)

車樹勤

函數的零點充分體現了函數與方程的聯系，蘊含了豐富的數形結合思想.諸如方程根的問題、存在性問題以及交點問題等都可以轉化為零點問題來討論，因而函數的零點成了近年來高考新的熱點而備受青睞.下面以一道蘇錫常鎮的高三調研試題為例來剖析函數的零點問題的解題方法.

一、考題回放

調研試題若函數f(x)=ax-x2(a>1)有三個不同的零點，則實數a的取值范圍是________.

思維階段求一個函數的零點個數，通常是轉化為我們熟悉的兩個函數看其圖像的交點個數，就是零點的個數.而本題的兩個函數是y=ax,y=x2，要使兩個函數圖像有三個交點則要使這兩個圖像在(0,+∞)有兩個交點.指數函數和二次函數的圖像都是曲線，該如何讓其有兩個交點是解決問題的關鍵.

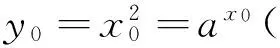
點評：本解是結合函數圖像，根據兩個函數圖像要有三個交點，明顯在第二象限有一個交點，在第一象限要有兩個交點.根據相切的時候有公共切線，切線斜率相等，以及該切點滿足兩個函數關系式列方程，求出相切時候a的值得到其取值范圍.

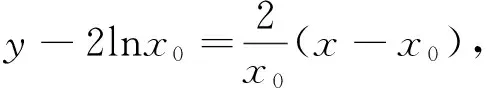
點評：本解法是先取對數后得到方程xlna=2lnx，要使其有兩個解，可看作兩個函數的圖像有兩個不同的交點，臨界狀態是一次函數與對數式函數相切的時候有一個交點，當直線的斜率變小時，兩函數圖像有兩個不同的交點，從而得到a的取值范圍.

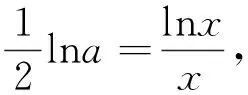
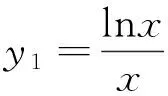
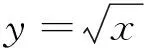
點評：本解法主要是利用互為反函數的函數圖像關于y=x對稱，所以兩個函數圖像原來有幾個交點，其反函數的圖像交點個數不變.方程ax=x2中的x在指數位置，由反函數轉化為對數來求.要求方程有兩根，在函數圖像先減后增的情況下，只要函數的極小值小于零即可.

本題從多個視角對函數零點問題進行了研究.思維1直接從兩個函數圖像有一個交點時進行探究；思維2先對方程取對數轉化為兩個函數再進行探究；思維3是把思維2中的方程再變形為一個關于x的函數與一個常數函數進行探究；思維4是利用反函數來看其交點個數.問題的關鍵在于轉化，把未知轉化為已知，希望通過此題的解答能在解題時打開思路，多角度進行思考，能起到事半功倍的效果.

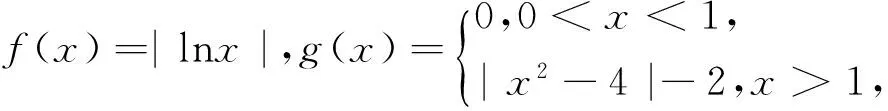
分析：分兩種情況去掉絕對值，再把f(x),g(x)的解析式代入方程，畫圖像看其交點個數.

解：(法一)由題意得：求函數y=f(x)與y=1-g(x)交點個數以及函數y=f(x)與y=-1-g(x)交點個數之和，因為y=1-g(x)=

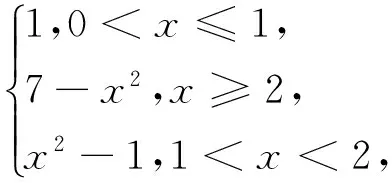
(法二)f(x)+g(x)=

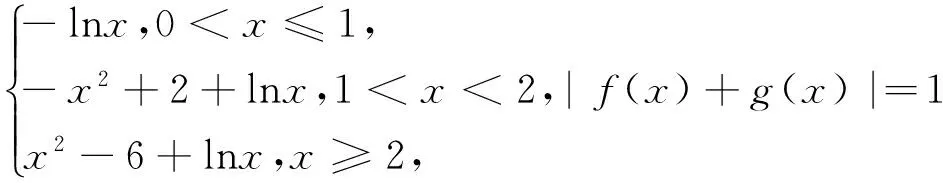
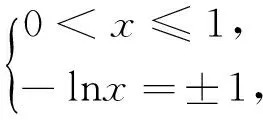
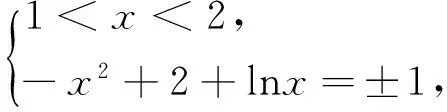
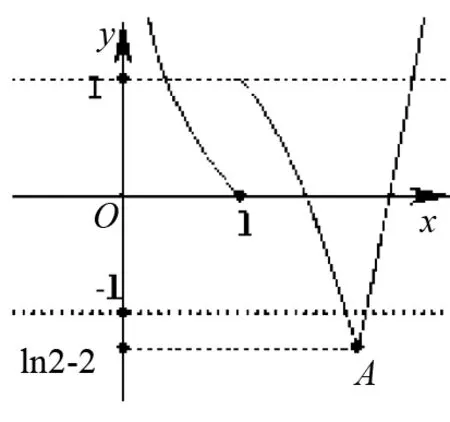
圖1

(3)考察

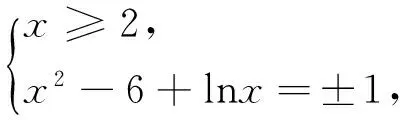
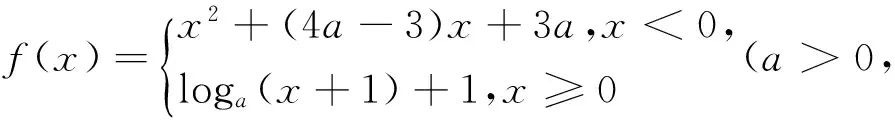
分析：利用函數是減函數，根據對數函數的圖像和性質判斷出a的大致范圍，再根據f(x)為減函數，得到不等式組，利用函數的圖像，方程的解的個數，推出a的范圍.

解：y=loga(x+1)+1在[0,+∞)遞減，則0

二、如何把握函數零點的教與學

從以上近兩年的高考函數的零點出現的題型總結分析，我認為在函數的零點教學中應當讓學生理解函數的零點的概念及定理，以及能掌握函數的零點題型的解題思路及常見方法.

1.函數的零點的存在性定理

如果函數y=f(x)在區間[a,b]上的圖像是連續不斷的一條曲線，并且有f(a)f(b)<0，則函數y=f(x)在區間(a,b)內有零點，即存在c∈(a,b)，使得f(c)=0，這個c也就是方程f(x)=0的根.零點存在性定理是函數在某區間上存在零點的充分不必要條件，此定理的逆命題不成立.

2.掌握函數的零點題型的解題思路及常見方法

從以上近兩年高考函數的零點題型的分析可以看出，高考對函數的零點問題主要考查以下三個層面：一是利用函數的零點的概念及定理求函數零點的個數及零點所在的范圍，這是基礎；二是給予一些函數零點的條件，確定其中未知的參數，這是基礎內容的提高；三是將函數的零點問題同其他知識結合在一起出綜合試題.不論高考如何命題，只要在函數的零點問題的教學中夯實基礎，立足課本，掌握函數的零點題型的解題思路及常見方法，注意函數的零點問題與函數、方程、圖像等其他知識的交叉融合，就能更好地培養學生綜合分析問題的能力及邏輯思維能力.