也談齊次化方法在圓錐曲線中的應用
2017-01-20 05:34:27深圳大學數學與統計學院518060
中學數學研究(江西) 2017年1期
關鍵詞:方法
深圳大學數學與統計學院 (518060)
關麗娜* 曹麗華
也談齊次化方法在圓錐曲線中的應用
深圳大學數學與統計學院 (518060)
關麗娜*曹麗華
圓錐曲線中常見于一類問題,這類問題的特點是條件中的兩直線斜率之和或之積是一個指定常數.這種問題的求解方法多種多樣,但是采用齊次化方法,可以將這兩種題型統一處理.接下來談談齊次化方法在處理圓錐曲線這些問題中的應用.
1.處理兩直線斜率之積為常數的問題


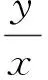
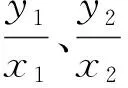
現在我們假設(2)式是存在的,那么有Ay2+Bxy+Cx2=0.(3)
也就是說我們需要從已知條件得到(3)式這樣一個關于x、y的2次齊次等式,于是便有了下面的齊次化方法:
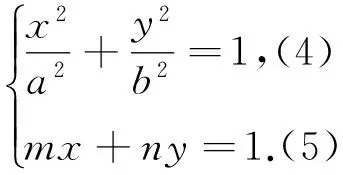
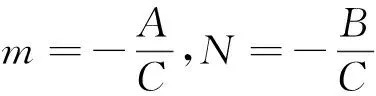

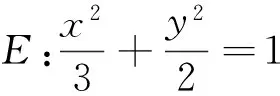
(1)求直線PA與PB的斜率之積;
(2)設直線l交橢圓E于M,N兩點,且以MN為直徑的圓恒過點A.求證直線l恒過定點,并且求出此定點的坐標.
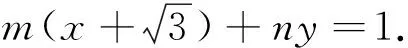

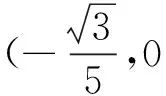
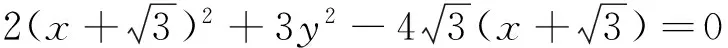
2.處理兩直線斜率之和為常數的問題
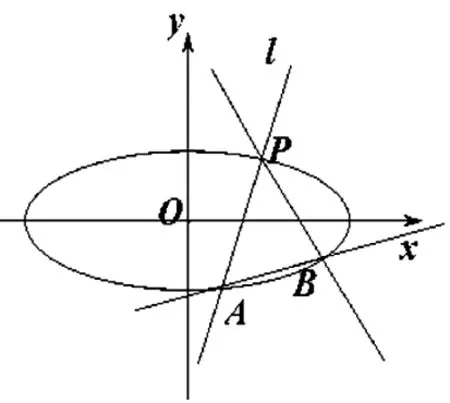
圖1
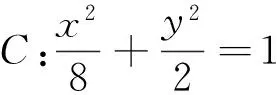

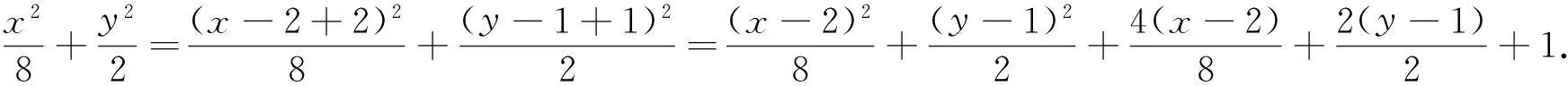
評注:從上面的解答過程可以看到,條件中斜率之間的關系可以推導出直線方程中m,n之間的一個關系式.
3.處理與斜率之和或者斜率之積相關的問題
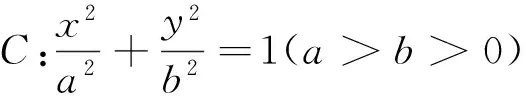
(1)求橢圓C的方程;
(2)設不過原點O的直線l2與該橢圓交于P、Q兩點,滿足直線OP,PQ,OQ的斜率依次成等比數列,求ΔOPQ面積的取值范圍.


余下略.
[1]徐守軍.巧構“齊次式”解一類解析幾何問題[J].廣東教育(高中版),2008:21-23.
* 作者現為碩士研究生,本文通訊作者為曹麗華老師.
猜你喜歡
中老年保健(2021年9期)2021-08-24 03:52:04
河北畫報(2021年2期)2021-05-25 02:07:46
中學生數理化(高中版.高考理化)(2020年2期)2020-04-21 05:33:04
兒童繪本(2020年5期)2020-04-07 17:46:30
兒童故事畫報(2019年5期)2019-05-26 14:26:14
Coco薇(2016年2期)2016-03-22 02:42:52
山東青年(2016年1期)2016-02-28 14:25:23
Coco薇(2015年1期)2015-08-13 02:47:34
小雪花·成長指南(2015年7期)2015-08-11 15:03:12
小雪花·成長指南(2015年4期)2015-05-19 14:47:56

