《常量與變量》課堂實錄（節選）

《常量與變量》課堂實錄（節選）

科 目 數 學

執教者李 玲/湖北省武漢市經濟技術開發區第一初級中學教師、高級教師

點評者翟立安/上海市數學特級教師

教學目標

1.在具體情境中領悟常量與變量的含義，能分清實例中的常量與變量。

2.用運動的眼光觀察生活，關注一個量隨另一個量變化而變化的現象。

3.感受“萬物皆變”，保持對世界的敏感和好奇，感知規律的普遍存在。

制造一次糾結

師：我這里有一個圓柱體的水槽，可以求它的容積嗎？

生：可以，V=Sh（S是水槽的底面積，h是水槽的高度）。

師：現在向水槽中注水，水槽里發生了什么變化？

生：水面不斷上升，水越來越多，……

師：在注水的過程中，水的體積可以求嗎？（學生開始“糾結”）

生：能，因為水槽中的水是圓柱體，用V=Sh就可以計算了。

生：不能，注水的過程中，水面高度不斷上升，體積逐漸變大，不能求。

師：觀點不同，但并不矛盾，只是所站的角度不同，看問題的眼光不同。

用運動變化的眼光看，注水的過程，水面的高度不斷上升，體積也隨著變化。

用靜態的眼光看，上升中的每個時刻都可以測量一個高，有一個確定的體積。

小結：我們習慣于計算一個杯子的容積，計算一次運動的路程，計算一次購物的總金額，我們總在追求計算一個結果。然而，當用運動的眼光去觀察時，我們看到的就是量與量之間的聯系，或者說是規律。

板書：

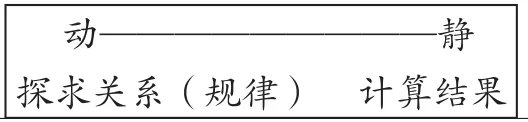
【意圖：制造一次“糾結”，經歷動與靜的沖突。】

點評：

這個引入比較妙！一是因為它是生活中常見的情景；二是因為它是從靜態很自然地走向動態；三是因為蘊含了本課的關鍵要素；四是因為一靜一動，引發了學生的比較與思考，產生了“糾結”引發了學生探究的興趣。

關注一類現象

師：在一個變化過程中，數值發生變化的量叫變量，保持不變的量叫常量。

當S一定時，V隨h的變化而變化，其中，S是常量，h和V是變量。

當h取一個值時，V有一個值與之對應。

（用幾何畫板動態演示）

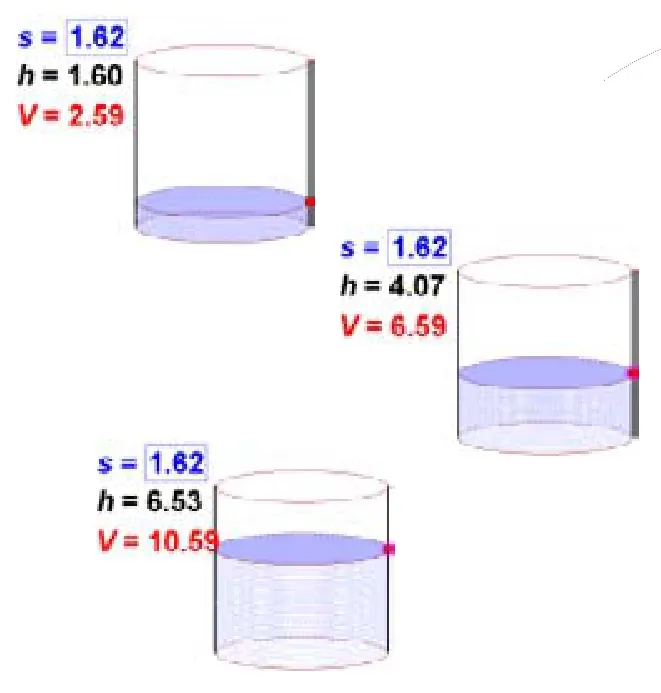
點評：

數學學習經常要經歷“具象、表象、抽象”這三個環節，有時是具體的形象在前，再到表象然后抽象；也可以先給出抽象的概念，再用具體的形象來解釋或演示，讓學生多感性地感悟。這里的幾何畫板演示，就起到了在出示概念后用學生對具象的感悟對概念的理解。

師：生活中廣泛存在著一種現象：一個量隨另一個量變化而變化，看下面例子，指出其中的變量和常量。

（1）下表反映了一家的奶茶店的銷售情況。

銷量X(杯) 1 2 3 4 5 6 7 ……銷售額Y(元) 6 12 18 24 30 36 42 ……

變量_____，常量____；____隨____的變化而變化。

（2）下圖表示了一天之中，____隨____的變化而變化，變量____，常量____。

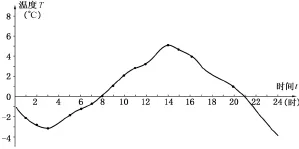
（3）以速度v0(m/s)向上拋一個小球，小球的高度h(m)與小球的運動時間t(s)之間的關系式為：h=v0t-4.9t2。在這一變化過程中，____隨____的變化而變化，變量____，常量____。

（學生產生疑惑：兩個人拋球，v0或許不相同，v0是常量還是變量？）

師：當理解模糊，產生疑問時，請“回到定義上去”。

生：不同的人拋球，表示不同的變化過程中，就好比（1）中我家的奶茶6元一杯，你家的奶茶8元一杯，而6和8都是各自變化過程中的常量。

（學生關注到了定義中的“在一個變化過程中”的前提，并用更容易理解的例子來打比方解釋，領悟到字母不一定就表示變量，為學生點贊。）

點評：

學生所以能夠有如此精彩的回答，是因為老師的啟發到位，“請回到定義”給學生思考指引了方向。數學概念教學要緊扣概念中的條件與結論，甚至要逐字逐句地分析概念的內涵，尤其是對關鍵詞的重點思辨。

小結：兩個變量之間的關系的表達形式可以是（1）中的表格，可以是（2）中的圖像，可以是（3）中的解析式，也可以用語言來描述。

點評：

選擇的三個生活中的現象，很典型，也比較全面，為后續學習函數打下良好的伏筆。

【意圖：關注一類現象，聚焦概念的理解。】

保持一份敏感

師：“萬物皆變”——行星在宇宙中的位置隨時間而變化，氣溫隨海拔而變化，樹高隨樹齡而變化……在你周圍的事物中，這種一個量隨另一個量的變化而變化的現象大量存在，請你繼續舉例，并指出其中的常量和變量。

生：加油過程中，油費隨汽油數量的變化而變化；股價隨時間的變化而變化；心電圖人體的生物電波隨時間的變化而變化；圓面積隨半徑的變化而變化；勻速運動中，路程隨時間的變化而變化……

（學生又回到往圓柱體水槽中注水的例子，水的壓強隨水的高度的變化而變化；水的重力隨水的高度變化而變化。)

【意圖：保持一份敏感,喚醒對世界的好奇。】

點評：

讓學生舉例，是判斷學生是否真正理解概念的一種方法，能夠正確舉一反三者，是理解概念者，只要不是機械模仿。

完成一次探索

師：一種手機卡有兩種收費方式。（接聽免費）

A套餐：月租費22元，撥打每分0.2元；

B套餐：無月租費，撥打每分0.4元。

請你為客戶制作一份選擇方案。

（學生獨立思考以后展開討論）

生1：B套餐合算，因為不用交月租費。

生2：我不同意，如果打200分鐘，B套餐收80元，A套餐只要62元。

我認為有時候A套餐劃算，有時候B套餐劃算

生3：費用跟撥打的時間有關，時間不一樣費用就不一樣。

生4：費用隨撥打時間的變化而變化，可以設撥打時間為x分。

0.2x+22=0.4x，x=110

當每月撥打時間≤110分時，選B套餐；

當每月撥打時間≥110分時，選A套餐。

作業：溫度隨海拔高度的變化而變化，具體關系如下：T=a-0.65h。

a表示海平面處的氣溫攝氏度，h表示海拔高度的百米數，T表示在h高度處的溫度。僅僅使用溫度計，能估算一座較高的山的高度嗎？

【意圖：完成一次探索，認識研究的必要。】

點評：

探索手機套餐問題，用來說明研究的必要性，最好能與本節課所學“常量”“變量”緊密相連。例如：師生合作分析時要注意突出不同套餐是不同的“一個變化過程”，要分析出常量、變量。當學生產生了方程“0.2x+22=0.4x”，老師要追問“如何想到利用方程來解決的？”因為這是兩個變化過程中尋找一個費用相等的時間常量。

講述一段史實

師：400年前，德國天文學家開普勒發現了行星運行的三大定律，破譯了天體運動的運行規律。人們按照開普勒定律觀測天王星時，發現它的實際運行軌道出現了偏差，猜想一下會是什么原因造成的？

生：因為另一個量的變化而變化。

點評：

這里學生回答含糊，到底是那個量的變化引起了另一個量的變化？教師要追問到讓幾乎讓所有學生都明白的地步，要生發出集體思維的“共振”，讓學習在每個學生身上真正地發生！

師：的確如此，根據天王星軌道的偏差推算出，并成功地觀測到了海王星，這顆利用掌握的規律進行數學運算發現的行星，被稱為“筆尖下的星球”。在此基礎上牛頓發現了更為普適的萬有引力定律，把地面上物體運動的規律和天體運動的規律統一起來，我們也不禁驚嘆，浩瀚的銀河系，共同遵循著同一條規律有序地運動變化。

常量變量帶我們走進了真實的運動變化的生活，希望同學們永遠保持對世界的驚訝與好奇，用數學的眼光和方法去解開更多的規律，探索更多的奧秘。

點評：

整個教學設計，非常自然流暢，流淌在學生的最近發展區，又引發學生合作探討的興趣，體現了教師較高的數學素養和教學設計的獨具匠心。

【意圖】講述一段史實，展望課題遠景。

設計思路

李玲/文

常量和變量是函數的萌芽，本節課是為函數的學習埋下一顆種子。我設計了五個問題，但答案得由學生給出。

問題一制造了一次“糾結”，“糾結”中學生經歷了動與靜的沖突。從靜態的常量數學到動態的變量數學，學生看問題的角度和眼光、思維方式都將發生深刻的變化。

問題二動態直觀地讓學生關注到一種現象：一個量隨另一個量變化而變化，這是本節課的核心。一方面常量變量是在這一現象中定義的；另一方面現象的本質就是函數，舉例過程中，有解析式、表格、圖像，讓學生提前感知了函數表達的三種形式，為后續學習作鋪墊。

問題三請學生大量舉例，加深對概念理解的同時希望他們保持對世界的關注和好奇。孩子小時候都特別喜歡問“為什么”，隨著年齡的增長，問題就變少了，是問題都解決了？更可能是司空見慣了，這種麻木要引起重視和警醒。

問題四在真實的問題情境中定方案、做決策，學生是用方程解決的問題，方程思想是動中求靜，研究運動中的等量關系，和函數思想有著密切的聯系。問題的解決讓學生進一步認識到生活是運動變化的，變化的問題是有辦法去研究的。

問題五講述了海王星的發現過程，無論是科學領域，還是人類社會的發展都依賴于對規律的逐步揭曉和利用，驚奇和震撼讓對學生對后續的學習滿懷期待。

義務教育階段的數學課講授的是最基礎的數學知識，是人類歷經幾千年的智慧結晶。當我欣喜地、精確地與學生分享我的所知、所思、所得時，他們卻未必能精確地接受，更談不上欣喜。于是我開始研究我的學生，這個過程讓我充滿了“共情”的能力，我也在學生和學科之間找到了一條“浪漫”的路徑：用合適的問題開啟學生的思考，學生自己悟到的才真正屬于自己。

知識本身固然是知識，在解決問題的過程中所積累下的活動性經驗又何嘗不是知識呢？它是學生面對未知，走向未來的知識和力量。