數學定理教學方法
——以“相似三角形判定定理1”為例

☉浙江象山縣石浦中學鄔云德

數學定理教學方法
——以“相似三角形判定定理1”為例

☉浙江象山縣石浦中學鄔云德

一、背景介紹

定理是用推理的方法判斷為正確的命題，它包括數學中的性質定理、判定定理、公式等.定理與原理“一字之差”，但邏輯形式卻有天壤之別.原理教學主要是由特殊到一般的歸納推理，定理教學主要是由一般到特殊的演繹推理；原理主要接受實踐的檢驗，定理必須經過邏輯的證明；原理教學可以借用“概念形成”的方式來進行，定理教學要經歷“提出問題→操作觀察→歸納猜想→分析證明→多樣表達→解決問題→反思內化”的過程.但在以浙教版數學九年級上冊第四章第4節“相似三角形的判定定理1”為載體的“多人同課異構”式的研修活動中發現，課堂教學普遍沒有遵循定理教學的基本規范.網上查閱同類課例發現也有類似現象.鑒于此，筆者在重復式觀課與反思的基礎上，對該課的教學進行重建，改進后的教學過程與效果得到了同仁的認可.現將其整理出來，以饗讀者.

二、教學實錄

環節1：經歷回顧并提出問題的過程——明確研究問題.

師：我們在研究兩個三角形全等的判定時，用分類探索的策略和用畫圖與實驗來證實（或用推理方法來證明）的方法，獲得了判定兩個三角形全等除定義外，還有“SSS”“SAS”“ASA”“AAS”“HL”等方法.由于全等三角形是相似三角形的特殊情況，判定兩個三角形相似除定義外，是否也有類似的判定方法？本節課我們類比研究兩個三角形全等的判定方法來研究兩個三角形相似的判定方法（.揭示課題）

環節2：探索三角形相似的條件——生成相似三角形判定定理1.

師：有一個角對應相等的兩個三角形相似嗎？為什么？

生1：不一定相似.例如，含60°角的直角三角形與含45°角的直角三角形不相似.

師：不錯.否定結論只要舉個反例即可.有兩個角對應相等的兩個三角形相似嗎？

師：若不能肯定或否定的話，請先依次完成下列任務.

（1）在白紙上畫一個△ABC.

（2）作一個△A′D′E′，使∠A′=∠A，∠D′=∠B.

（3）議一議：△A′D′E′與△ABC是不是相似三角形？（待學生完成任務）

師：△A′D′E′與△ABC是不是相似三角形？

生2：好像相似.但說不出它們對應邊成比例的理由.

師：雖然不能完全肯定，但可以提出這樣的猜想：有兩個角對應相等的兩個三角形相似.下面我們來證明這個猜想是正確的.現在請大家先依次完成下列任務.

（1）在所畫的圖形上標注已知條件.

（2）結合圖形寫出已知與求證.

（待學生完成任務）

師：如圖1，要證明△A′D′E′∽△ABC，只要證什么？

生3：因為∠A′=∠A，∠D′ =∠B，∠E′=∠C，所以只要證

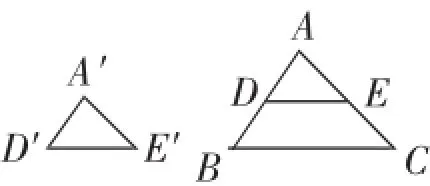
圖1

師：有道理，現在只能依據相似三角形的定義.我們學過的哪個結論與比例線段有關？

生4：由平行線截得的比例線段的基本事實與比例線段有關.

師：好的.如圖1，若在△ABC中能作一個△ADE，使△A′D′E′≌△ADE，則要證△A′D′E′∽△ABC，只要證△ADE∽△ABC.能作一個△ADE，使△A′D′E′≌△ADE嗎？

生5：能.因為∠A′=∠A，在AB上截取AD=A′D′，作DE∥BC，交AC于點E，則∠ADE=∠B=∠D′，所以△A′D′E′≌△ADE（ASA）.

師：好的.因為DE∥BC，所以可得哪些結論？

生6：因為DE∥BC，所以∠ADE=∠B，∠AED=∠C，

（眾生困惑、期待）

，所以△ADE∽△ABC.又△A′D′E′≌△ADE，所以△A′D′E′∽△ABC（相似三角形的傳遞性）.

師：下面請大家按這樣的思路把證明過程完整地寫出來.

（待學生完成任務）

師：這樣我們得到了如下的相似三角形判定定理1：

有兩個角對應相等的兩個三角形相似.

師：在證明過程中還可得以下結論（課本中稱它為預備定理）：

平行于三角形一邊的直線和其他兩邊相交，所構成的三角形與原三角形相似.師：怎樣用幾何語言來表示相似三角形判定定理1？生7：在△A′D′E′和△ABC中，若∠A′=∠A，∠D′=∠B，則△A′D′E′∽△ABC.

師：好的.請大家課后用幾何語言來表示預備定理.證明判定定理1的基本思路是什么？

生8：根據相似三角形的傳遞性，通過構造全等三角形來證明.

生9：通過構造全等三角形把分散的條件集中起來.

師：有道理.我們根據相似三角形的傳遞性，用構造全等三角形的方法實現化歸.這種化歸思想以后會經常用到.

環節3：參與定理應用的活動——合作解決有代表性的問題.

師：現在我們一起解決下列問題.

問題：在一次數學活動課上，為了測量河寬AB，小聰采用了圖2所示的方法：從A處沿與AB垂直的直線方向走45m到達C處，插一根標桿，然后沿同方向繼續走15m到達D處，再右轉90°走到E處，使B、C、E三點恰好在一條直線上.量得DE＝20m，這樣就可以求出河寬AB.請你說明理由，并算出結果.

師（稍停頓后）：誰來說明理由并計算其結果？

圖2

生10：因為AB⊥AD，DE⊥AD，所以∠BAC=∠EDC=90°.因為B、C、E三點在一條直線上，所以∠ACB=∠DCE.所以△ABC∽△DEC（有兩個角對應相等的兩個三角形相似），所以又

答：河寬AB是60m.

師：好的.解決這個問題經歷了哪幾個基本步驟？

生11：先根據已知條件判定兩個三角形相似，再用相似三角形的性質來計算.

師：解題的關鍵是什么？

生12：根據相似三角形的性質列出合適的方程.

師：好的.在幾何計算中，經常要運用方程思想.能用同樣的道理，再設計幾種測量河寬AB的方法嗎？請大家合作研討.

（約4分鐘后）

師：誰來匯報設計的方案？

生13：如圖3，只要CD∥AB，使A、C、E三點共線，B、D、E三點共線，并量出AC、CE、CD的長、就能求出AB的長.

生14：如圖4，在BA的延長線上取點D，在AB的右側取點C，連接AC，過點D作DE∥AC，交BC的延長線于點E，并量出AC、DE、AD的長，就能求出AB的長.

圖3

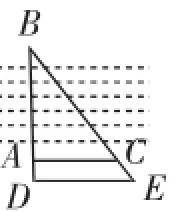
圖4

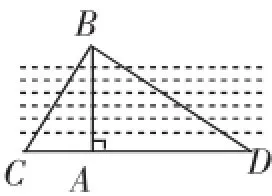
圖6

生15：如圖5，只要DE∥AB，使A、C、D三點共線，B、C、E三點共線，并量出AC、CD、DE的長，就能求出AB的長.

生16：如圖6，只要BA⊥CD，∠C+∠D=90°，并量出CA、AD的長，就能求出AB的長.

師：太有才了！這些都是可行的方法.下面請大家完成課本中的練習題.

（待學生完成任務后教師組織學生交互反饋與評價）

環節4：參與回顧與思考的活動——合作進行反思與總結.

師：本節課研究了哪些內容？

生17：本節課研究了相似三角形判定定理及其應用.

師：好的.我們是怎樣研究的？

生18：先探索并證明判定定理1，再用判定定理1解決實際問題.

師：不錯.發現判定定理1的策略與方法分別是什么？

生19：策略是分類討論，方法是畫圖、推理.

師：好的.這是發現數學結論常用的經驗.

師：大家在學習過程中還有哪些收獲或體會？

生20：三角形按相似的規則變化時，對應角的度數保持不變.

師：不錯.圖形的相似具有保持對應角度數不變的性質.

生21：分類討論是發現數學結論的基本策略.

生22：只要∠A′=∠A，就可以在△ABC中作一個△ADE，使△A′D′E′≌△ADE.

生23：化不熟悉的問題為熟悉的問題是解決問題的重要思想方法.

生24：用相似三角形知識能解決許多實際問題.

生25：用傳遞性證兩個三角形相似時，只要△A′D′E′∽△ADE即可.

生26：盡管測量河寬的方法具有多樣性，但要選擇簡單的方法.

生27：根據相似三角形的性質可列出多個方程，但要選擇合適的方程.

師：好！這些收獲與體會非常有價值，對后繼學習有指導作用.

三、教學分析

探索與證明相似三角形判定定理1的思想方法對后繼學習有指導作用.定理的探索與證明的過程和所蘊含的歸納思想、化歸思想、演繹思想等，用定理解決實際問題的過程和所蘊含的數形結合思想、方程思想等及測量河寬的多樣化設計方案，這些對發展學生的智力、能力和個性有積極的影響.目前在該課的教學中，大多數教師沒有體現分類探索的策略；有些教師探索判定定理和證明定理之前的分析過程短暫；大多數教師在獲得判定定理和解決實際問題之后缺乏必要的反思；大多數教師在認知過程中沒有留給學生充足的自主思考與實踐的時間和合作交流的機會.

本課例在“精致化”分析基礎上，改變課本先講預備定理再講判定定理1的做法，將其教學立意于過程教育，并從學生已有的知識與經驗出發，運用教師價值引導與學生自主建構相結合的適度開放的方式，引導學生經歷完整的認知過程.在“回顧并提出問題”的教學中，既有回顧研究兩個三角形全等的判定的思想方法，以激活研究全等三角形判定的數學活動經驗，又有提出問題的過程，以建立新舊知識之間的內在聯系和激發學生的學習興趣.在“探索并證明判定定理1”的教學中，既有借助已有經驗進行“分類探索→畫圖猜想→分析證明→多樣表達”的過程，以獲得判定定理1和預備定理及發展探索與證明的能力，又有獲得判定定理之后的反思，以內化用構造全等三角形來實現化歸的思想方法，積累用相似三角形的傳遞性和構造全等三角形來證三角形相似的新經驗.在“定理應用”的教學中，既有引導學生解決給定問題的過程，以鞏固所學的知識和發展智慧技能，又有解決問題之后的反思，以認識用相似三角形知識解決實際問題的思想方法，還有開放式設計測量河寬方案的過程，以發展學生的發散思維能力和想象能力，積累測量河寬等方案的數學活動經驗.在“回顧與思考”的教學中，既有回顧研究內容，又有回顧研究方法，還有學生談學習后的收獲與感受.

參與研修的教師普遍認為，本課例遵循了定理教學的基本規范，體現了過程教育和以學為中心的思想，統籌兼顧了過程與結果，能實現教學目標.一般地，定理教學要經歷“提出問題→操作觀察→歸納猜想→驗證或證明→多樣表達→解決問題→反思內化”的過程，并在組織實施數學活動時，留給學生足夠的自主思考與實踐的時間和合作交流的機會，發揮教師在數學活動中的主導作用，合理評價學生在數學活動過程中的表現，以促使學生對定理的認識達到一定的“深度”和“寬度”，促使學生學會主動提出問題，獨立思考問題，合作探究問題，以及養成敢于質疑、善于表達、認真傾聽、勇于評價和不斷反思的良好品質和習慣.

教學實踐表明，在定理教學中，要實現知識、技能、能力、態度的完美統一，需要教師增強揭示定理所蘊含的思維活動過程的自覺性，而引導學生經歷實質性思維過程需要教師充分貫徹啟發式教學思想.以符合“最近發展區”理論的題材為載體，從學生已有的知識與經驗出發，運用教師價值引導與學生自主建構相結合的適度開放的方式，能使學生經歷過程中的思維站點，從而能促進學生全面、和諧發展.本課例在農村中學實施后，發現時間有點兒緊張，可見體現過程教育的課堂教學會對按時完成教學任務帶來挑戰.解決這個問題的策略：一是運用課內外結合的方法——課前預習教師設計的“導學案”；二是根據學生的現實來確定過程與結果的平衡點——結果是主要的、基本的，相對來說過程是次要的、從屬的.

1.中華人民共和國教育部制定.義務教育數學課程標準（2011年版）［S］.北京：北京師范大學出版社，2012.

2.范良火.義務教育教科書數學（九年級上冊）［M］.杭州：浙江教育出版社，2014.