基于高維動態(tài)藤Copula的匯率組合風(fēng)險分析

韓 超，嚴太華

(重慶大學(xué)經(jīng)濟與工商管理學(xué)院，重慶 400044)

基于高維動態(tài)藤Copula的匯率組合風(fēng)險分析

韓 超，嚴太華

(重慶大學(xué)經(jīng)濟與工商管理學(xué)院，重慶 400044)

以Pair Copula為簡單構(gòu)造模塊的高維動態(tài)藤Copula結(jié)構(gòu)能夠克服二元Copula面臨的“維度詛咒”問題,對多元變量之間的非線性相依進行動態(tài)化描述，是Copula函數(shù)研究的學(xué)術(shù)前沿。本文選取美元、歐元、日元、港幣及英鎊五種匯率的日間對數(shù)收益率數(shù)據(jù)實證研究,對其進行AR-GJR-GARCH模型過濾，過濾所得新息序列用GPD模型擬合，之后進行概率積分變換，采用高維動態(tài)C藤和D藤Copula對變換后序列建模，運用蒙特卡羅方法計算組合風(fēng)險VaR,對其進行UC回溯測試，并與相應(yīng)的靜態(tài)方法作比較。結(jié)果表明：高維動態(tài)C藤Copula結(jié)構(gòu)計算出來的VaR表現(xiàn)最好，對其進行分解發(fā)現(xiàn)美元的邊際風(fēng)險最低，通過蒙特卡羅選擇權(quán)重組合發(fā)現(xiàn)最大限度持有美元將會產(chǎn)生最小VaR。該結(jié)論為量化風(fēng)險指標、合理配置資產(chǎn)，及風(fēng)險監(jiān)管提供了一種新的模型與方法。

AR-GJR-GARCH模型；高維動態(tài)藤Copula；匯率組合風(fēng)險；VaR；UC回溯測試

1 引言

1973年，以“雙掛鉤”形式為特征的布雷頓森林體系終究因為“特里芬兩難”積重難返而瓦解，其后，浮動匯率體制大行其道。浮動匯率制在使各國獲得“不可能三角”另外兩極的同時，也加劇了國際貿(mào)易與國際金融的匯率風(fēng)險，國際間的風(fēng)險傳染變得難以計量和掌控，匯率風(fēng)險也因此成為學(xué)術(shù)領(lǐng)域的研究熱點。

在匯率風(fēng)險研究中，單一維度的匯率風(fēng)險計量并不能適應(yīng)存在錯綜復(fù)雜關(guān)系國際匯率間的內(nèi)在要求，傳統(tǒng)的以線性相關(guān)為基礎(chǔ)的二維或者多維匯率組合風(fēng)險計量又無法真實把握匯率風(fēng)險之間的非線性相依和時變相依特征。基于此，許多學(xué)者開展了相關(guān)的研究，其中以二元或者多元Copula函數(shù)為研究方法的文獻較為常見，比如：吳振翔等[1]，Patton[2]，柏滿迎和孫祿杰[3]，茍紅軍等[4]。

然而，傳統(tǒng)的二元Copula函數(shù)會面臨“維度詛咒”問題，傳統(tǒng)的多元Copula函數(shù)又會因為只能采用同一種Copula的某一兩個參數(shù)去描述多元變量之間的復(fù)雜相依關(guān)系而受到限制。為了突破這種局限，學(xué)者們開始了Copula函數(shù)高維化和動態(tài)化的前沿研究，其中，高維動態(tài)藤Copula以Pair Copula為簡單構(gòu)造模塊，能夠彌補傳統(tǒng)二元或者多元Copula的缺陷，對多元變量之間的非線性相依關(guān)系進行靈活地動態(tài)化描述，相關(guān)的研究有：So和Yeung[5],Reboredoa和Andrea[6],葉五一等[7],杜子平等[8]。

鑒于以上，本文運用最新的高維動態(tài)藤Copula方法研究匯率組合風(fēng)險問題。研究中采用AR-GJR-GARCH模型對原始序列進行過濾，對過濾所得新息序列用GPD模型進行概率積分變換(PIT)，之后運用高維動態(tài)藤Copula進行多元動態(tài)相依建模。在理論分析的基礎(chǔ)上，選取美元、歐元、日元、港幣及英鎊五種匯率的日間對數(shù)收益率數(shù)據(jù)為研究對象，對其進行邊際分布和相關(guān)性結(jié)構(gòu)的擬合與檢驗，運用蒙特卡羅模擬方法對動態(tài)和靜態(tài)情形進行比較，最后進行VaR的邊際風(fēng)險和最小VaR的資產(chǎn)組合權(quán)重研究。研究結(jié)論對于投資決策、風(fēng)險管理和風(fēng)險資本配置等具有參考意義。

2 理論基礎(chǔ)

2.1 藤Copula基本理論

根據(jù)Sklar[9]的定義，Copula本質(zhì)上是描述變量的連接函數(shù)。在給定信息集F[t-1]時，rit,i=1,2,…,p的條件聯(lián)合累積分布及其密度函數(shù)可以分別表示為式(1)(2)：

(1)

(2)

式(2)借助于藤結(jié)構(gòu)形式可以分解成一系列的二維Copula，以規(guī)則藤中最常見的C藤和D藤為例，二者的p維密度函數(shù)可以分別表示為式(3)(4)：

(3)

(4)

式(1)-式(4)中的Copula及C藤和D藤Copula函數(shù)可以用邊際分布與Copula聯(lián)合表達，二者建模可以分離進行，計算上更為可行，稱之為“兩階段建模”。“兩階段建模”為進一步利用藤Copula對多維風(fēng)險變量的組合風(fēng)險計量提供了可能，本文借助于C藤和D藤Copula方法開展匯率組合風(fēng)險研究。

2.2 高維動態(tài)藤Copula構(gòu)建

高維動態(tài)藤Copula的構(gòu)建需要進行藤的類型選擇。以規(guī)則藤中最常見的C藤和D藤為例，二者的類型選擇取決于多維變量之間有無關(guān)鍵變量，也就是與其他變量之間的相關(guān)關(guān)系是否壓倒性的超過其他變量之間的關(guān)系。C藤或D藤確定以后，需要進行藤的排列，第一棵樹的排列尤為重要，它決定了之后樹的結(jié)點和邊的構(gòu)造。對于第一棵樹，C藤需要將關(guān)鍵變量置于根部，其余變量按照與根部的緊密關(guān)系依次排列；D藤也面臨著變量之間相關(guān)強度大小的問題，依據(jù)相關(guān)度大小排列成對變量，據(jù)以構(gòu)成樹形圖，需要注意的是D藤中當(dāng)一個變量被選擇兩次的時候，它不能在第一棵樹上形成新的Pair Copula對。按照規(guī)則藤的定義，無論C藤還是D藤，樹j的邊是樹j+1的結(jié)點，樹j的邊的數(shù)量與樹j+1結(jié)點的數(shù)目相同，樹j擁有共同節(jié)點的兩條邊在樹j+1上是相連的，第一棵樹確定了，其余樹的順序也就依次得出了。

藤的類型與排列確定以后，就進入了藤的擬合階段。由式(3)(4)，C藤和D藤的構(gòu)建過程中條件分布函數(shù)F[t]起到了關(guān)鍵作用。對于C藤和D藤來說，F(xiàn)[t]的計算方式有很大差異，分別為式(5)、式(6)：

(5)

(6)

這種差異使得同樣的F[t]函數(shù)表達式，C藤和D藤計算的最終結(jié)果將截然不同。本文主要以成對t-Copula研究高維動態(tài)藤Copula結(jié)構(gòu)，其F[t]函數(shù)及參數(shù)都是時變的，可以表示為式(7)：

(7)

(8)

(9)

則式(9)就可以求出動態(tài)h函數(shù)值，其中vt表示時序t的隨機向量，ν-j,t是剔除掉第j個變量的vt向量。

以動態(tài)h函數(shù)為中介函數(shù)，循環(huán)往復(fù)地求解藤Copula每棵樹的參數(shù)，步驟如下：

②從第二棵樹開始，上一棵樹的邊即連接結(jié)點的Copula函數(shù)，采用動態(tài)t-copula，動態(tài)參數(shù)為動態(tài)表達式(8)的參數(shù)，根據(jù)動態(tài)h函數(shù)式(9)求得h序列，作為下一棵樹的結(jié)點數(shù)據(jù)；

③直到最后一棵樹,迭代運算步驟②，可以計算出每棵樹上的h函數(shù)的參數(shù)及對應(yīng)的動態(tài)化h序列，這就完成了整個藤的構(gòu)建。

在形式上C藤結(jié)構(gòu)較之D藤要復(fù)雜，其實，D藤無論是構(gòu)建、擬合，還是仿真都比C藤復(fù)雜、困難，這源于二者的F[t]函數(shù)求解式(5)和式(6)的不同。

2.3 高維動態(tài)藤Copula仿真

C藤和D藤Copula結(jié)構(gòu)的仿真算法形式上相同，以五維為例，都有式(10)：

x1t=w1t

(10)

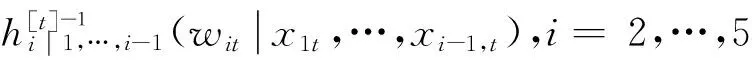
x1t=w1t

(11)

x1t=w1t

(12)

無論對于高維動態(tài)C藤還是D藤的數(shù)據(jù)仿真，計算過程都應(yīng)該是動態(tài)化的，動態(tài)參數(shù)由相應(yīng)的動態(tài)型h函數(shù)和時變Copula函數(shù)求得，動態(tài)參數(shù)服從式(8)中的動態(tài)演進式。為了更為直觀的表達仿真計算過程，分別畫出x5t在C藤和D藤中的仿真路徑圖，如圖1和圖2，其中C藤和D藤h逆函數(shù)的條件變量剔除次序是相反的。圖中，W5為w5t的集合向量，X5為x5t的集合向量。

圖1 動態(tài)C藤Copula的仿真路徑圖

圖2 動態(tài)D藤Copula的仿真路徑圖

2.4 VaR與回溯檢驗

VaR表示資產(chǎn)收益率序列在顯著性水平α下的分位數(shù)。求解VaR有歷史模擬法、方差-協(xié)方差方法和蒙特卡羅模擬法等。本文結(jié)合研究實際借助Matlab編程采用蒙特卡羅模擬方法，按照擬合的藤結(jié)構(gòu)仿真多維數(shù)據(jù)，倒推出模擬收益率序列，每10000個數(shù)據(jù)模擬實現(xiàn)之后，通過計算機按照相應(yīng)的顯著性水平自動選擇位于數(shù)據(jù)排序左端的對應(yīng)數(shù)據(jù)作為此10000個數(shù)據(jù)組的1個VaR值，如此得出包含400個元素的VaR的隨機序列組，將其與樣本外400個數(shù)據(jù)分別進行返回檢驗，觀察比較高維動態(tài)藤Copula與高維靜態(tài)藤Copula的風(fēng)險效果。VaR的這一回溯檢驗是通過R語言來編程實現(xiàn)的，理論基礎(chǔ)是Kupiec[11]的UC檢驗。

3 計算路徑與模型

本文采用兩階段建模方法擬合藤結(jié)構(gòu)，通過h逆函數(shù)對藤Copula結(jié)構(gòu)進行數(shù)據(jù)仿真，這一過程涉及到若干次建模與計算，計算路徑可以分解為以下步驟：

①用AR-GJR-SkewT模型對多元收益率序列進行過濾，模型表示如式(13)所示：

zit=σit·εit

εit～i.i.dST(λi,ηi)

(13)

其中λi,ηi分別表示SkewT分布的偏斜度和自由度。

②對①中的新息序列進行雙尾GPD極值建模，模型如式(14)所示：

i=1,2,3,4,5

(14)

③對PIT序列進行動態(tài)PairCopula建模，求出相應(yīng)的時變相關(guān)系數(shù)序列，對其求均值。這里主要采用的是Pair-t-Copula函數(shù)，模型表示為式(15)所示，其中，uit,ujt均表示成對PIT序列元素，令xt=(xit,xjt)′，則：

(15)

④比較高維PIT序列的兩兩相關(guān)系數(shù)均值，分析是否存在主導(dǎo)變量，以確定藤的類型和關(guān)鍵變量，如果存在主導(dǎo)變量，則采用C藤。

⑤分別以C藤和D藤作比較研究，擬合邊和節(jié)點的參數(shù)，方法參照2.2節(jié)內(nèi)容。

⑥根據(jù)⑤中藤Copula的動態(tài)參數(shù)仿真PIT序列，仿真過程中需要進行動態(tài)h逆函數(shù)的倒推與求解，對于t-Copula來說，h逆函數(shù)可以表示為式(16)：

(16)

⑦對⑥中的動態(tài)仿真PIT序列按照②①的結(jié)構(gòu)進行返回倒推，即可求出高維動態(tài)相關(guān)收益率序列。

⑧對動態(tài)收益率序列按2.4節(jié)蒙特卡羅方法計算VaR值，并且進行樣本外返回檢驗。

⑨分析邊際VaR，求解最小VaR的資產(chǎn)組合權(quán)重。

4 實證研究

4.1 數(shù)據(jù)預(yù)處理

本文以美元(USD)、港幣(HKD)、歐元(EUR)、英鎊(GBP)和日元(JPY)五種外匯為研究對象，時間區(qū)間從2007年1月4日到2015年8月25日，取日間對數(shù)收益率Ri,t=ln(Pi,t/Pi,t-1)為研究指標，其中，P表示匯率的中間價，i=1,2,3,4,5，分別表示USD、EUR、JPY、HKD和GBP五種外匯，共2102組數(shù)據(jù)。前1702組五維數(shù)據(jù)為樣本內(nèi)數(shù)據(jù)，用來模型擬合，后400組數(shù)據(jù)用來進行VaR的樣本外返回檢驗。全文數(shù)據(jù)建模與分析借助于Matlab、R語言、SPSS等軟件實現(xiàn)，數(shù)據(jù)取自中國貨幣網(wǎng)的外匯中間牌價。表1為五維序列的特征統(tǒng)計表，顯見五維數(shù)據(jù)的尖峰厚尾性，Jarque-Bera統(tǒng)計量強烈拒絕正態(tài)性假定，同時數(shù)據(jù)分布具有左偏特性。

表1 五維匯率收益率特征統(tǒng)計表

4.2 平穩(wěn)性檢驗

平穩(wěn)性是金融時間序列建模和預(yù)測的前提，本文運用模型對數(shù)據(jù)進行過濾之前必需對數(shù)據(jù)進行平穩(wěn)性檢驗，相應(yīng)的單位根ADF檢驗結(jié)果如表2所示，可見五種金融時間序列的ADF值都遠遠突破了1%、5%、10%顯著性水平的臨界值，均強烈拒絕單位根存在的原假設(shè)，沒有理由認為五種金融時間序列不是平穩(wěn)時間序列。

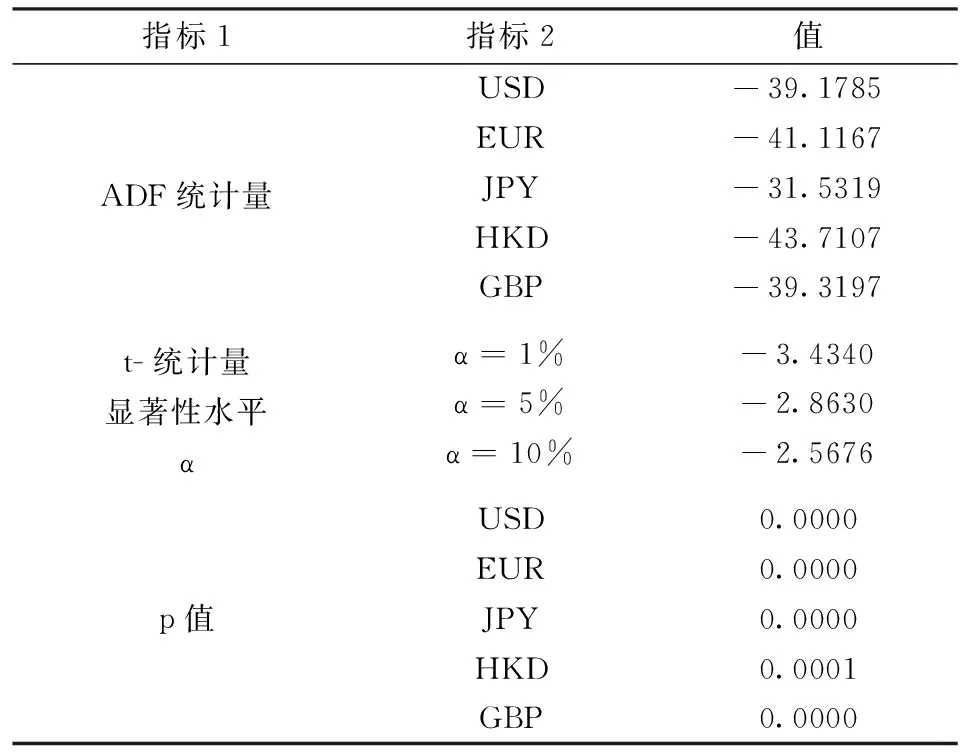
表2 日對數(shù)匯率收益率平穩(wěn)性檢驗表

4.3 獨立性檢驗與波動性聚類判別

Brock、Dechert和Scheinkman[12]基于關(guān)聯(lián)積分的定義提出了BDS檢驗統(tǒng)計量，并且證明在獨立同分布的原假設(shè)下該統(tǒng)計量滿足漸近的標準正態(tài)分布。基于此，本文采用BDS檢驗方法檢驗五種金融時間序列的獨立同分布特征，檢驗結(jié)果表明，五種金融收益率序列BDS檢驗的p值均為0，拒絕了獨立同分布原假設(shè)，需要進一步的數(shù)據(jù)處理。為了進一步檢驗并且證實這一點本文接下來進行原始序列和平方序列的自相關(guān)檢驗。以美元(USD)和歐元(EUR)為例，繪制自相關(guān)圖3和圖4。從圖中可以發(fā)現(xiàn)輕微程度的序列相關(guān)和波動持久記憶特征，說明存在GARCH效應(yīng)，4.4.1節(jié)中采用AR-GJR-GARCH模型消除這一特征，取得了較好的效果。

圖3 匯率收益率的自相關(guān)圖

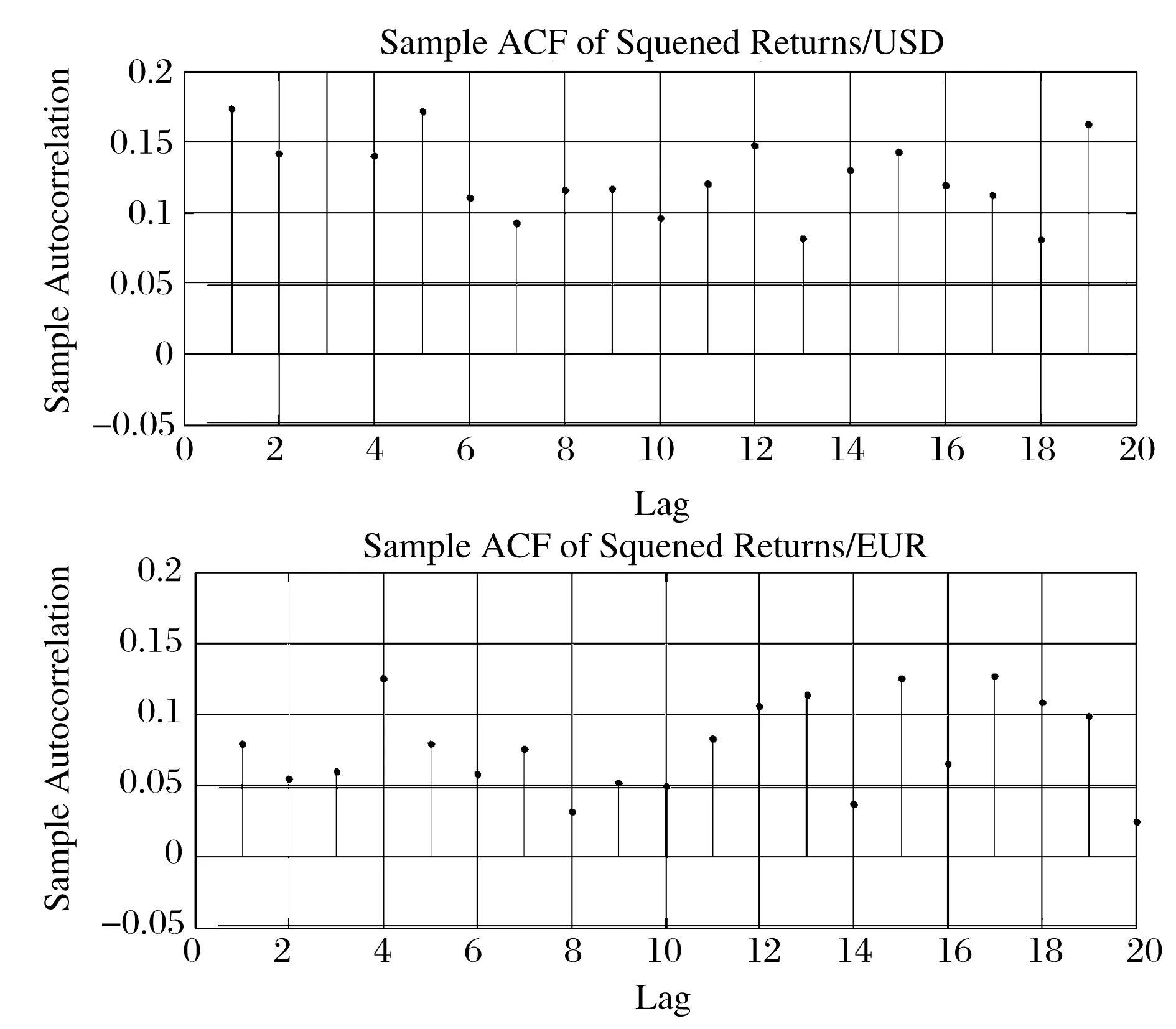
圖4 匯率收益率的平方自相關(guān)圖

4.4 單個時間序列的模型提煉與數(shù)據(jù)過濾

McNeil等[13]的研究表明：如果金融時間序列非獨立，但滿足平穩(wěn)性條件，在一定的弱相依條件下，仍然可以應(yīng)用極值模型，若要采用極值模型則要求大致符合獨立同分布條件。但以上檢驗結(jié)果表明：五種匯率收益率序列均具有平穩(wěn)性但不具獨立性，有輕微的序列相關(guān)性和偏斜特征，存在GARCH效應(yīng)。因此，本文采用AR-GJR-GARCH模型，通過標準化殘差過濾數(shù)據(jù)，生成大致符合獨立同分布的新息序列。

4.4.1 單個時間序列的模型提煉

本文采用AR-GJR-GARCH模型來對單個時間序列進行擬合。其中，AR模型用來消除單個金融序列的自相關(guān)，階數(shù)根據(jù)實際有所不同，GJR模型用來克服收益率序列的波動性聚類和正負新息沖擊的非對稱性特征，而偏斜t(Skew T)分布能夠準確描述序列的尖峰、厚尾和偏斜特性，解決模型過濾后標準化殘差分布存在的偏斜問題。

采用AR-GJR-GARCH模型對五維時間序列進行數(shù)據(jù)過濾，生成相應(yīng)的新息序列。對過濾所得的標準殘差序列分別繪制自相關(guān)圖和波動性聚類圖，以驗證模型的實際效果，仍以美元(USD)和歐元(EUR)為例，相應(yīng)的自相關(guān)檢驗和平方自相關(guān)檢驗結(jié)果見圖5和圖6，經(jīng)過與數(shù)據(jù)過濾前的原始序列及平方序列的自相關(guān)圖相比較，可以發(fā)現(xiàn)數(shù)據(jù)過濾消除了大部分自相關(guān)現(xiàn)象，對其進行BDS檢驗，在5%的顯著性水平下，五維序列也大致都能接受序列符合獨立同分布的原假設(shè)。這樣，過濾后的數(shù)據(jù)就基本達到了后續(xù)尾部極值擬合所要求的預(yù)定效果。

圖5 新息序列的自相關(guān)圖

圖6 新息序列的平方自相關(guān)圖

4.4.2 廣義帕累托分布(GPD)參數(shù)估計與擬合檢驗

4.5 高維動態(tài)藤Copula的參數(shù)估計

4.5.1 高維動態(tài)藤Copula的類型選擇

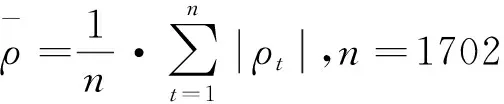
表3 GPD擬合參數(shù)及PIT檢驗表

表4 靜態(tài)t Copula函數(shù)兩兩相關(guān)比較表

表5 動態(tài)歸一化兩兩相關(guān)比較表

經(jīng)過靜態(tài)和動態(tài)的兩兩相關(guān)比較可以發(fā)現(xiàn)，沒有任何一個變量能夠處于絕對的強勢地位，如USD在與JPY和HKD的相關(guān)性上大于其余幾種外匯與JPY和HKD的相關(guān)性，而與EUR的相關(guān)性卻小于GBP，與GBP的相關(guān)性小于EUR，從這個角度來說，采用D藤擬合是合適的；然而進一步比較又可以發(fā)現(xiàn)美元(USD)處于相對主導(dǎo)地位，比如USD與EUR的比較，盡管USD與GBP的關(guān)系小于EUR與GBP，但是USD與JPY和HKD的相關(guān)均大于EUR與JPY和HKD的相關(guān)，類似的方法進行比較可以得出USD處于相對主導(dǎo)地位的結(jié)論，從這個角度來說，似乎采用C藤也可行。本文出于典型研究需要，分別采用C藤和D藤進行比較研究，得出二者中更為合適的類型，而對介于C藤和D藤之間的別的結(jié)構(gòu)形式不予考慮。

完成以上的工作后，接著進行藤Copula的排列。由表4和表5可以比較得出第一棵樹的變量排序：USD、HKD、EUR、GBP、JPY。按照2.2節(jié)中的排列方法可以分別繪制出C藤和D藤的結(jié)構(gòu)圖7和圖8。其中，數(shù)字1,2,3,4,5分別表示USD、EUR、JPY、HKD和GBP五種外匯匯率，Tj,j=1,2,3,4分別表示藤的第j棵樹，樹的數(shù)目比維度少1。

圖7 五維C藤排序結(jié)構(gòu)圖

圖8 五維D藤排序結(jié)構(gòu)圖

4.5.2 高維動態(tài)C藤和D藤Copula的擬合

高維動態(tài)C藤和D藤Copula是許多高維靜態(tài)C藤和D藤Copula的集合體，對于tCopula函數(shù)而言，假定相關(guān)參數(shù)是時變的，而自由度保持不變，按照2.2節(jié)的構(gòu)建方法，借助于Matlab編程就可以得到以h函數(shù)為構(gòu)成要素的動態(tài)C藤和D藤Copula函數(shù)的參數(shù)，如表6和表7所示。

表6 高維動態(tài)C藤Copula函數(shù)參數(shù)表

注：vij表示tCopula的自由度，αij、βij分別表示動態(tài)方程式(8)中的對應(yīng)參數(shù)；此表的h41和表7的h14參數(shù)相同，序列卻不同，原因在式(9)。

表7 高維動態(tài)D藤Copula函數(shù)參數(shù)表

注：因為擬合t Copula的自由度大于30，根據(jù)相關(guān)理論，Gaussian-Copula是t-Copula自由度很大時的特例，因此，的空格所在的h函數(shù)對應(yīng)的參數(shù)以Gaussian-Copula函數(shù)來擬合，此時自由度vij即為空值，有關(guān)Gaussian-Copula的理論參見韋艷華[16]。

4.6 高維動態(tài)C藤和D藤Copula函數(shù)的仿真與VaR測度

按照4.5節(jié)中藤的結(jié)構(gòu)和第3節(jié)的仿真方法進行數(shù)據(jù)仿真，分別以1%，5%和10%的顯著性水平，蒙特卡羅模擬得到相應(yīng)的VaR值序列，然后對其進行樣本外返回檢驗，比較不同方法對于組合風(fēng)險VaR計算的準確性。為了使研究更具有一般意義，本文隨機選取兩種組合比例分別為(20%，20%，20%，20%，20%)與(10%，30%，20%，10%，30%)，所產(chǎn)生的對應(yīng)的組合風(fēng)險序列分別為VaR1和VaR2。按照前述方法進行仿真，求得1%，5%，10%顯著性水平兩種比例的VaR序列，與相應(yīng)的樣本外數(shù)據(jù)比較，再運用Kupiec Test方法進行回溯檢驗，得到無條件覆蓋(UC)檢驗結(jié)論，結(jié)果如表8所示。

為了表述方便，我們把高維動態(tài)C藤簡稱為C動，其余類似推之。經(jīng)過比較可以發(fā)現(xiàn)對于VaR1而言，10%的顯著性水平上，接受概率C靜

表8 藤Copula回溯檢驗統(tǒng)計量表

值得注意的是，D動在每次檢驗中實際超越都不同程度的大于期望超越，甚至在5%顯著性水平下VaR1拒絕了原假設(shè)，這可能因為：在4.5.1節(jié)中首先進行的是藤的類型判定，為了研究更具典型性，從C藤和D藤兩種規(guī)則藤類型中選擇，經(jīng)過相關(guān)分析，嘗試性的分別采用C藤和D藤進行比較研究。而實際上結(jié)合國際貨幣制度的遷延史，自從二戰(zhàn)后布雷頓森林體系以雙掛鉤的形式確立美元霸主地位以來，盡管美元的國際地位有所下降，直到當(dāng)前仍是國際主要通用支付工具，美元相較于歐元、日元、港幣及英鎊，無疑是關(guān)鍵變量。而本文的研究進一步佐證了這一點，說明采用以美元匯率為關(guān)鍵變量的C藤Copula更為合適：表8中D動的表現(xiàn)則說明采用C藤比D藤更好，D動表現(xiàn)弱于D靜，說明如果模型選擇不準確，改進模型可能就會在錯誤方向上走得更遠；而表6的擬合效果明顯優(yōu)于表7，尤其是第三棵樹和第四棵樹的參數(shù)顯著性水平與對數(shù)似然值，輔助說明了C藤更為占優(yōu)。

以上分析說明：藤Copula用來風(fēng)險計量時需要進行優(yōu)化選擇，只有采用正確的模型種類，建模的分析效果才會更加準確。進一步從表8中可以發(fā)現(xiàn)：總體上C動模型最優(yōu)，且C動在5%和1%的顯著性水平下有過兩次概率為1的完美風(fēng)險捕捉；C動優(yōu)于C靜也驗證了動態(tài)模型由于更為精準的刻畫風(fēng)險之間的時變相關(guān)而優(yōu)于靜態(tài)模型。

5 VaR的分解與最小VaR的資產(chǎn)權(quán)重

風(fēng)險管理實踐中，僅僅對于組合風(fēng)險進行計量是不夠的，還必須了解投資風(fēng)險的內(nèi)部構(gòu)成、不同的組合權(quán)重VaR有何區(qū)別，及最小VaR所對應(yīng)的權(quán)重組合。為此，本節(jié)內(nèi)容從VaR的分解與VaR的資產(chǎn)組合權(quán)重兩個角度對高維動態(tài)C藤和靜態(tài)C藤Copula結(jié)構(gòu)計量的外匯組合風(fēng)險作進一步的研究。

5.1 VaR的分解

Hallerbach[17]系統(tǒng)研究了M-VaR(邊際VaR)、C-VaR(成分VaR)、I-VaR(增量VaR)的相關(guān)理論，指出C-VaR和I-VaR的求解可以通過M-VaR得到。因此，研究M-VaR有著特殊的意義。根據(jù)杜紅軍、胡海鵬、邵欣煒等[18-20]的研究，在正態(tài)分布假設(shè)下，組合期望回報為零時，有：

其中，VaR(P)為組合風(fēng)險，wi為第i種資產(chǎn)權(quán)重。按照這種計算方法，結(jié)合本文的研究實際，可以分別求出等權(quán)重和不等權(quán)重兩種風(fēng)險的VaR1和VaR2的邊際風(fēng)險，對其進行分析，認為：三種顯著性水平的C動和C靜都分別有USD的M-VaR最低，HKD次之，EUR的M-VaR最高，說明在追求更小VaR的過程中，文中的兩種資產(chǎn)組合都應(yīng)該增加USD，減持EUR等資產(chǎn)。但是這種判斷方法只能判斷局部的投資組合傾向，無法給出全局的最優(yōu)比例，為了得到最小VaR對應(yīng)的最優(yōu)資產(chǎn)權(quán)重組合，我們在5.2節(jié)中采用蒙特卡羅模擬進行全局最優(yōu)選擇。

5.2 最小VaR的資產(chǎn)組合權(quán)重

吳振翔等[1]基于靜態(tài)Archimedean Copula函數(shù)運用方差-協(xié)方差方法確定了二維匯率組合風(fēng)險最小VaR的投資組合，對于本文具有一定的啟示意義。不同的是，本文采用高維藤Copula方法蒙特卡羅模擬出靜態(tài)與動態(tài)的外匯組合風(fēng)險VaR,通過對不同組合比例的VaR進行比較，發(fā)現(xiàn)最小VaR對應(yīng)的權(quán)重組合，得出不同的分析結(jié)論。

本文進行VaR的資產(chǎn)組合權(quán)重分析，將會面臨資產(chǎn)組合選擇過多的問題。為了使研究更具可行性，假定五維外匯資產(chǎn)USD、EUR、JPY、HKD和GBP在組合中的資產(chǎn)權(quán)重分別為j,k,l,m,n，資產(chǎn)權(quán)重的選擇分別以0.1為步長，在0≤j,k,l,m,n≤1,j+k+l+m+n=1，且資產(chǎn)權(quán)重均為0.1整數(shù)倍的約束下，每10000次的仿真將會面臨：

次不同權(quán)重組合的VaR計算，然后對每1001次的VaR進行比較，找出給定顯著性水平α下的最小VaR及對應(yīng)的資產(chǎn)權(quán)重組合。表9是在不同的顯著性水平下，分別在1001個VaR中找到最小VaR值和對應(yīng)資產(chǎn)組合權(quán)重的結(jié)果，表明無論C動或者C靜，幾乎都主張將資產(chǎn)全部放在美元上，這與我們的經(jīng)驗也是相符的：美元是低風(fēng)險的外匯資產(chǎn)。

表9 不同α下的最優(yōu)權(quán)重組合

6 結(jié)語

本文以市場風(fēng)險中的匯率風(fēng)險為研究對象，針對匯率風(fēng)險因子之間可能存在的非線性相依情形，首先對高維時間序列進行AR-GJR-GARCH模型過濾，對過濾所得新息序列用GPD模型擬合，以擬合所得參數(shù)對五維新息序列概率積分變換，得到五維PIT序列。然后分別進行C藤和D藤的靜態(tài)和動態(tài)Copula擬合，按照擬合參數(shù)進行五維數(shù)據(jù)仿真，再依據(jù)過濾模型進行數(shù)據(jù)倒推，得出仿真收益率數(shù)據(jù)，按照兩種投資組合比例和三種顯著性水平分別得到包含400個元素的VaR值序列，對其進行UC回溯測試，發(fā)現(xiàn)高維動態(tài)C藤Copula結(jié)構(gòu)表現(xiàn)最好，更適合匯率組合風(fēng)險計量。最后結(jié)合M-VaR和蒙特卡羅方法研究了最小VaR對應(yīng)的資產(chǎn)權(quán)重組合，發(fā)現(xiàn)最大限度持有美元將會有效降低風(fēng)險VaR值。

論文所作的研究為投資決策、風(fēng)險管理和風(fēng)險資本配置及風(fēng)險監(jiān)管提供了一種新的計算思路與計量方法。

[1] 吳振翔,葉五一,繆柏其.基于Copula的外匯投資組合風(fēng)險分析[J].中國管理科學(xué),2004,12 (4):1-5.

[2] Patton A J. Modelling asymmetric exchange rate dependence[J].International Economic Review,2006,47(2):527-556.

[3] 柏滿迎,孫祿杰.三種Copula-VaR計算方法與傳統(tǒng)VaR方法的比較[J].數(shù)量經(jīng)濟技術(shù)經(jīng)濟研究, 2007,(02):154-160.

[4] 茍紅軍,陳迅,花擁軍.基于GARCH-EVT-COPULA模型的外匯投資組合風(fēng)險度量研究[J].管理工程學(xué)報,2015,9(1):83-193.

[5] So M K P,Yeung C Y T. Vine-copula GARCH model with dynamic conditional dependence[J].Computational Statistics and Data Analysis,2014,76:655-671.

[6] Reboredoa J C, Andrea U. Downside /upside price spillovers between precious metals: A vine copula approach[J].North American Journal of Economics and Finance,2015,34: 84-102.

[7] 葉五一,李瀟穎,繆柏其.基于藤Copula方法的持續(xù)期自相依結(jié)構(gòu)估計及預(yù)測[J].中國管理科學(xué),2015,23(11):29-38.

[8] 杜子平,閆鵬,張勇.基于“藤”結(jié)構(gòu)的高維動態(tài)copula的構(gòu)建[J].數(shù)學(xué)的實踐與認識,2009,39(10):96-102.

[9] Sklar A. Fonctions de répartition àn dimentions et leursmarges[J].Publication de I’Institut de Statistique de L’Universit-é de Paris:1959,8: 229-231.

[10] Aas K,Czado C,Frigessi A,et al. Pair-copula constructions of multiple dependence[J].Insurance：Mathematics & Economics, 2009,44(2): 182-198.

[11] Kupiec P.Techniques for verifying the accuracy of risk measurement models[J]. Journal of Derivatives,1995,3:73-84.

[12] Brock W, Dechert W, Scheinkman J.A test for independence based on the correlation dimension[R].Working Paper,University of Wisconsin at Madison, University of Houston,and University of Chicago,1987.

[13] Mcneil A J,Frey R．Estimation of tail-related risk measures for heteroscedastic financial time series：An extreme value approach[J]. Journal of Empirical Finance，1998,7(3-4):271-300.

[14] Pickands J. Statistical inference using extreme order statistics[J].The Ann als of Statistics, 1975,3(1):119-131.

[15] 韋艷華,張世英.Copula理論及其在金融分析上的應(yīng)用[M].北京:清華大學(xué)出版社,2008.

[16] Hallerbach W G. Decomposing portfolio value at risk:A general analysis[J]. Journal of Risk,2003,5(2):1-18.

[17] 杜紅軍,王宗軍. 基于Copula-AL法的VaR和CVaR的度量與分配[J].中國管理科學(xué),2012, 20(3):1-9.

[18] 胡海鵬,方兆本.投資組合VaR及其分解[J]. 中國管理科學(xué)，2003,11(3):1-5.

[19] 邵欣煒,張屹山. 基于VaR的證券投資組合風(fēng)險評估及管理體系[J].數(shù)量經(jīng)濟技術(shù)經(jīng)濟研究,2003,12:66-70.

Risk analysis of Foreign Exchange Portfolios Based on High-dimensional Dynamic Vine Copula

HAN Chao, YAN Tai-hua

(School of Economics and Business Administration, Chongqing University, Chongqing 400044, China)

The structure of high-dimensional dynamic vine copula can overcome ‘dimensional curse’ faced by bivariate Copula and dynamically describe nonlinear dependence between multi-variables, and represents the academic frontier. Five kinds of foreign exchange log-returns, including USD, EUR, JPY, HKD and GBP, are selected to make empirical analysis, Time series are fitted with AR-GJR-GARCH and GPD models. After probability integral transform, high-dimensional dynamic C and D vine copulas are modelled. Then, portfolio VaR sets are got by Monte-Carlo method, tested by UC back testing, and compared to the corresponding static research. The results show that VaR based on high-dimensional dynamic C vine copula performs the best, and marginal risk of USD is considered as the least by VaR decomposition, the more USD the lest risk. The conclusions provide a new model and method to quantify risk, reasonably allocate asset portfolio, and for authorities to regulate risk.

AR-GJR-GARCH model; high-dimensional dynamic vine copula; portfolio risk of foreign exchange; VaR; UC back testing

1003-207(2017)02-0010-11

10.16381/j.cnki.issn1003-207x.2017.02.002

2015-11-09；

2016-10-05

國家自然科學(xué)基金資助項目(71373296)

嚴太華(1964-),男(漢族),重慶璧山人,重慶大學(xué)經(jīng)濟管理學(xué)院,博士生導(dǎo)師,教授,研究方向:金融工程,E-mail:875071743@qq.com.

F830.9

A