讓“化歸”成為開啟數(shù)學的金鑰匙*—初中數(shù)學教學中滲透化歸思想的策略

廣東省佛山市南海區(qū)和順第一初級中學(528241) 李西華

讓“化歸”成為開啟數(shù)學的金鑰匙*—初中數(shù)學教學中滲透化歸思想的策略

廣東省佛山市南海區(qū)和順第一初級中學(528241) 李西華

匈牙利著名數(shù)學家P.羅莎(Rozar,Peter)在《無窮的玩藝》中寫道: “數(shù)學往往不是對問題進行正面攻擊,而是不斷對它進行變形,直到把它轉化成能夠解決的問題”.前蘇聯(lián)數(shù)學家雅諾夫思卡婭說: “解題――就是意味著把所要解的問題轉化為已經(jīng)解過的問題.”在初中數(shù)學中,有許多新知識的獲得或新問題的解決都是通過轉化為已知知識或已解決的問題來完成的,也就是將新知識向已知知識點或知識塊轉化,從而使問題得到解決.解決某些數(shù)學問題時,如果直接求解較為困難,可通過觀察、分析、類比、聯(lián)想等思維過程,運用恰當?shù)臄?shù)學方法進行變換,將問題轉化為一個新問題(相對來說較為熟悉的問題),通過新問題的求解,達到解決原問題的目的.這一思想方法我們稱之為“化歸的思想方法”.化歸思想,就是在研究和解決有關數(shù)學問題時采用某種手段將問題通過變換使之轉化,進而達到解決的一種方法.一般總是將復雜問題通過變換轉化為簡單問題;將難解的問題通過變換轉化為容易求解的問題;將未解決的問題通過變換轉化為已解決的問題.化歸的基本功能是: 生疏化成熟悉,復雜化成簡單,抽象化成直觀,含糊化成明朗.化歸思想是中學數(shù)學最基本的思想方法,是一切數(shù)學思想方法的核心,畫如下結構圖學生易于理解:

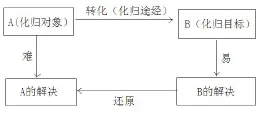
圖1

皮亞杰說過: “一切有成效的工作必以興趣為先決條件.”興趣是最好的老師,是學生積極創(chuàng)造的驅動力,是創(chuàng)造思維活動的成功先導.為了提高學生學習化歸思想的興趣,對于初學者,老師也可以講“曹沖稱象”、匈牙利著名數(shù)學家P.羅莎的“數(shù)學家燒開水”等典故來闡述數(shù)學化歸思想方法及其功用.下面主要從滲透化歸思想的策略方面進行研究.

一、尋找滲透化歸思想的孕育點

數(shù)學思想教學要經(jīng)歷多次孕育階段.學生學習數(shù)學思想存在潛意識性,潛意識的作用是緩慢的、漸進的,所以要反復孕育,而且對于復雜的、難度較大的思想方法,孕育的次數(shù)也相應多些.(以初三為例)例如(1)一元二次方程轉化為一元一次方程;(2)相似多邊形的性質: 周長的比、面積的比化歸為相似比來解決;(3)三角形的中位線定理的證明問題化歸為特殊四邊形中的問題來解決;(4)相似三角形問題: 通過作輔助線,把相似三角形中的一些問題化歸為基本圖形,A型、X型、母子型等來解決;(5)將多邊形內(nèi)角和問題化歸為三角形內(nèi)角和問題;(6)將特殊四邊形問題化歸為全等三角形問題;(7)將相似三角形問題化歸為對應線段成比例問題;(8)將四邊形四邊中點問題化歸為三角形中位線問題等等.

例三角形的中位線定理的證明問題化歸為特殊四邊形中的問題來解決.

八年級學習了平行四邊形的性質和判定及三角形全等的性質和判定.

①確定目標: DE//BC,且DE=BC=?平行四邊形?(原因: 平行四邊形的對邊平行且相等)

②尋找差異: 無法直接找到平行四邊形.

③消除差異: 按如下圖添加輔助線,構造平行四邊形,易得解.

再如初中數(shù)學“有理數(shù)的減法”,教材是通過學生自主探究和合作交流,經(jīng)歷把有理數(shù)的減法轉化為加法的過程,從而得出“減去一個數(shù)等于加上這個數(shù)的相反數(shù)”,這個地方雖然很簡單,但卻充分體現(xiàn)了把“沒有學過的知識”轉化為“已經(jīng)學過的知識”來加以解決,學生一旦掌握了這種解決問題的策略,今后無論遇到多么難、多么復雜的問題,都會有意識想到把“不會的”轉化為“會的”知識來加以解決,這符合學生原有認知規(guī)律,作為教師,我們不能因為簡單而忽視它的教學,實踐告訴我們,往往是越簡單、淺顯的例子,越能引起學生的認同,所以我們不能錯過這一絕佳的滲透化歸思想的機會.

總之,數(shù)學思想是數(shù)學的精髓.作為數(shù)學老師,深度鉆研教材,充分挖掘內(nèi)隱的數(shù)學思想,采取有效的策略,使之顯化于教學之中,“流淌”在數(shù)學課堂之內(nèi)外.

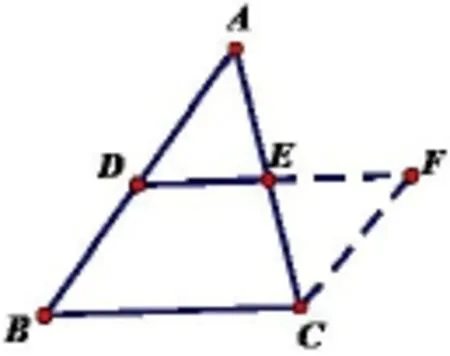
圖2

圖3

圖4

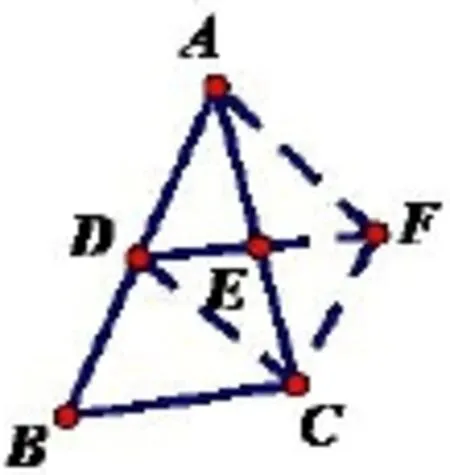
圖5

二、在慢化教學中滲透化歸思想

慢化教學是針對學生的認知特征和學習水平而采用的有效性過程,從而等待學生領悟的實用性教學理念,其目的是借助慢化教學的平臺讓學生有角度切入、有時間思考,能聽得懂、學得會,進而從學會到想學、會學、樂學.慢化教學不是為慢而慢,更不是消極怠工,而是為了生成“快”的效果而采取的“緩慢”策略,其最終目的是為學生提供更為廣闊的、更為自由的、更為適切的學習空間.

例: 證明: 如果一個三角形是直角三角形,那么這個三角形斜邊上的中線等于斜邊的一半.

已知: 在Rt△ABC中,∠ABC=90°,D是斜邊AC上的中點.

老師布置上課的前一天晚上先預習,接著課堂上讓學生進行小組討論,為了使學生更易于了解、領悟、內(nèi)化數(shù)學化歸思想,筆者采用慢化教學中滲透化歸思想的策略,取得了較理想的效果.

三、滲透常見的化歸方法

化歸思想方法用在研究、解決數(shù)學問題時,思維受阻或尋求簡單方法或從一種狀況轉化到另一種情形,也就是轉化到另一種情境使問題得到解決,這種轉化是解決問題的有效策略,同時也是成功的思維方式,初中階段常見的化歸方法有:

(1)直接轉化法: 把原問題直接轉化為基本定理、基本公式或基本圖形問題.

例 如: 如圖,已知 菱 形BEDF內(nèi)接于△ABC,點E、D、F分別在AB、AC和BC上,若AB=15,BC=12,求菱形的邊長.

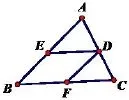
圖6

分析: 通過利用菱形的四邊都相等,對邊平行的性質,把求菱形邊長的問題直接轉化為證一對基本圖形(A字形)相似的問題,即△AED∽△ABC,再利用相似三角形的性質對應線段成比例求出菱形的邊長.

(2)換元法: 運用“換元”把式子轉化為有理式或使整式降冪等,把較復雜的函數(shù)、方程、不等式問題轉化為易于解決的基本問題.

(3)數(shù)形結合法: 研究原問題中數(shù)量關系(解析式)與空間形式(圖形)關系,通過互相變換獲得轉化途徑.

例如: 二次函數(shù)與一元二次方程的關系

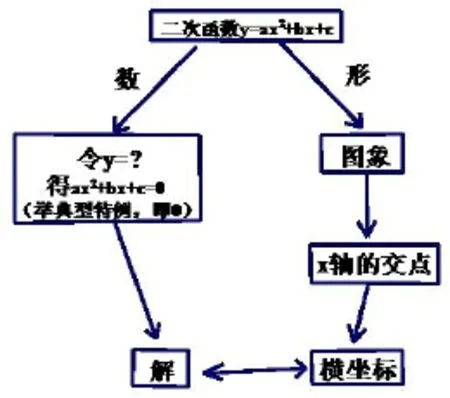
圖7

建立如圖所示思維導圖,通過“數(shù)”與“形”的互相轉化、“特殊”與“一般”的轉化,很好的揭示了二次函數(shù)與一元二次方程的關系,使學生易于理解.

(4)等價轉化法: 把原問題轉化為一個易于解決的等價命題,達到化歸的目的.

例如：如圖,在Rt△ABC中,E為斜邊AC上一點, AE=2,EC=1,四邊形DEFB為正方形,則陰影部分的面積為___.

分析: 將直角三角形EFC繞E點,按逆時針方向旋轉,因為BDEF是正方形,所以EF和ED重合,C點落在BD上,陰影部分的面積轉化為直角三角形AGE的面積,因為AE=2,EC=1,所以陰影部分的面積易求得為1.

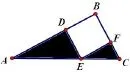
圖8

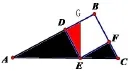
圖9

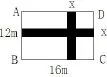
圖10

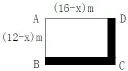
圖11

(5)特殊化方法: 把原問題的形式向特殊化形式轉化,并證明特殊化后的問題、結論適合原問題.一般問題特殊化,使問題處理變得直接、簡單.特殊問題一般化,可以使我們從宏觀整體的高度把握問題的一般規(guī)律,從而達到成批的處理問題的效果.

(6)構造法: 構造法就是根據(jù)題設條件或結論所具有的特征和性質,構造滿足條件或結論的一個合適的數(shù)學模型,把問題變?yōu)橐子诮鉀Q的問題.

例如: 解非特殊角的三角函數(shù)問題: 求tan22.5°的值.

解: 構造如圖所示的Rt△ABC,∠C=90°,設AC= DC=1,則延長CD到B,使則

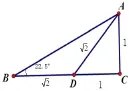
圖12

分析: 本題從22.5°是45°的一半著手思考,從大腦儲存庫里調運出特殊三角形等腰直角三角形的其中一個底角是45°想到構造一個等腰直角三角形,通過延長再構造一個以等腰直角三角形的斜邊為腰的等腰三角形,它的底角即為22.5°,從而把“數(shù)”的問題向“形”的問題轉化,順利得解.

四、用不同呈現(xiàn)方式滲透數(shù)學化歸思想

(1)要素化式: 確定化歸對象,確定化歸目標,尋找差異,確定化歸方法,消除差異.特點是具體、明了,學生易懂,適合方程、方程組、不等式等內(nèi)容的教學.

(2)結構圖式: 結構網(wǎng)絡化,條理清晰,直觀、易懂,適合方程、方程組、不等式、幾何證明等內(nèi)容的教學以及教學小結、反思.

例2: 解方程組:

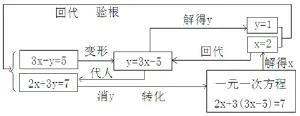
圖13

五、教會學生進行解題后的反思

羅增儒教授認為反思就是從自身的認識活動中“脫身”出來,作為一個“旁觀者”來看待自己剛才做了些什么事情,使自己的活動成為了思考的對象.有兩個層面的回顧反思,一個是解題層面的回顧反思(已高度關注),另一個是學會解題層面的回顧反思(想知道很多又有很多不知道).教師可以教會學生從以下幾方面進行反思: ①體現(xiàn)了哪些數(shù)學思想方法?②用到了哪些數(shù)學知識?③存在哪些困難?④解法有沒有可以改進的地方?⑤積累了哪些數(shù)學活動經(jīng)驗?⑥你能否把這一方法用于其它問題?等等.

六、給學生一個化歸思想的“創(chuàng)客”空間

啟迪智慧,開拓想象空間,快樂學習,智慧人生.給學生一個數(shù)學思想的“創(chuàng)客”空間,學生會給你一個意想不到的結果.比如在“創(chuàng)客”空間里讓學生嘗試挖掘數(shù)學課本中隱含化歸思想的例題、習題解題思路、定理的證明方法;網(wǎng)上搜索有關化歸思想的學習文章、隱含或運用化歸思想的題目;小組合作嘗試編制有關數(shù)學思想方面的簡單小題目;小組評選數(shù)學思想研究“小專家”,帶領自己的研究團隊來了解、認識數(shù)學思想,進而領悟、研究數(shù)學思想;每小組在“小專家”帶領下開展數(shù)學思想“一幫一”活動;每周由一個小組簡單匯報本小組的數(shù)學思想研究的情況;定期在宣傳欄展示學生的優(yōu)秀研究成果,定期舉辦交流分享活動,你可以聆聽別人的分享和經(jīng)驗,也可以分享自己的創(chuàng)意,展示自己的作品,招募小伙伴一起實現(xiàn)創(chuàng)意.如下是學生在化歸思想的“創(chuàng)客”空間的部分作品.

學生學習數(shù)學不僅要學習它的知識內(nèi)容,更要學習它的精神、思想和方法.為此,在數(shù)學教學中,要善于挖掘教材中蘊含的化歸思想方法,不斷總結化歸法解題的一般原理、提煉蘊含其中的思想方法,把化歸思想方法的教學融于各個環(huán)節(jié)之中,讓學生切實感受到化歸思想方法的存在形式及其發(fā)揮的作用;還要特別強調解決問題以后的“反思”,因為在這個過程中提煉出來的數(shù)學思想方法,對學生來說才是易于體會、易于接受的;更要注意滲透的長期性,因為數(shù)學思想方法是在啟發(fā)學生思維過程中逐步積累和形成的,數(shù)學思想方法在教學中的滲透必須經(jīng)過循序漸進和反復訓練,才能使學生真正地有所領悟.

*本文是董磊主持的廣東省教育科學“十二五”規(guī)劃2011年度立項課題“如何在初中數(shù)學教學中滲透數(shù)學思想方法的實踐研究”(課題批準號: 2011TJK014)的研究成果之一.