近年高考題中含參不等式恒成立問題的求解策略
廣東省廣州市恒福中學(510075) 張美鈺
近年高考題中含參不等式恒成立問題的求解策略
廣東省廣州市恒福中學(510075) 張美鈺
恒成立問題,是指在綜合給定的范圍內無論如何變化,某些數學問題的結論都不會發生任何改變.高中數學的恒成立問題是高考的一種重要題型,它涉及到函數、數列、不等式、導數等諸多方面的知識,同時考查了學生分析問題、解決問題、綜合駕馭知識的能力.求解含有參數的恒成立問題是常見的題型,也是高考的熱點.這類問題既含參數又含變量,可以考察到學生的思維能力和對數學知識的融會貫通的情況,在近年高考中出現頻率較高.本文根據近三年的高考題總結了三種含參不等式恒成立問題的求解策略.
策略一、分離變量求解
1.(2016年江蘇高考卷文理第 19題)已知函數f(x)=ax+bx(a>0,b>0,a/=1.b/=1).
(i)求方程f(x)=2的根;
(ii)若對于任意x∈R,不等式f(2x)≥mf(x)-6恒成立,求實數m的最大值;
(2)(略)
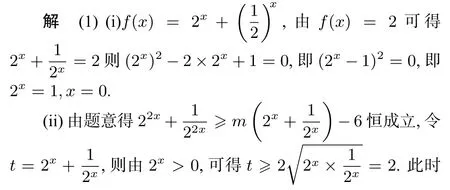
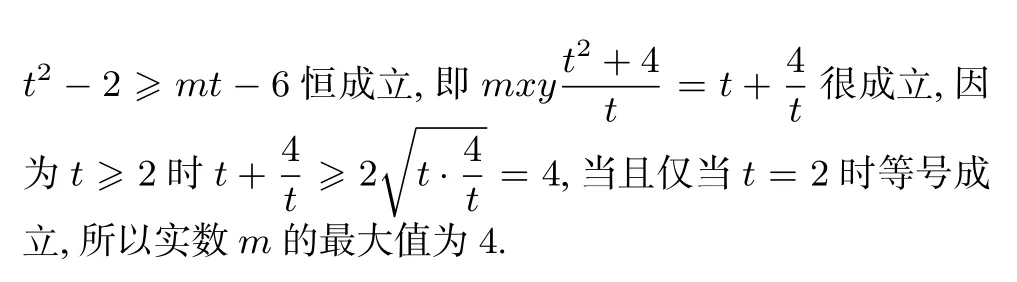
對于一些含參的不等式恒成立問題,如果能夠將不等式進行同解變形,將不等式中的變量和參數進行分離,即使變量和參數分別位于不等式的左、右兩邊,那么通過求函數值域的方法將問題化歸為解關于參數的不等式問題.應該說,這種解題思想是高中比較常規的一種思想.一般地有:

2.(2014年遼寧高考文科第12題、理科第11題)當x∈[-2,1]時,不等式ax3-x2+4x+3≥0恒成立,則實數a的取值范圍是( )

此題的解決思想仍是分離變量,將不等式恒成立問題轉化為函數的最值與參量的大小比較,而此題要求在分離變量時對x的范圍進行分類討論,否則會出錯.
策略二、構造函數求解
(1)求證: f(x)≤0;


x (0,x0) x02 g′(x) + 0 -g(x)↗↘

當參數難以分離時,可以通過構建函數來解決.我們知道,函數概念是高中數學的一個很重要的概念,其思想和方法已經滲透到數學的各個分支.在有些數學問題上中,通過觀察數式特點,構造適當的數學模型,然后通過研究此函數性質來確定參數的取值范圍.
4.(2016年全國新課標 I卷文第 12題)若函數f(x)=x-+asinx在(-∞,+∞)單調遞增,則 a的取值范圍為( )


此題作為選擇題的壓軸題,并沒有直接給出一個二次函數考查,而通過換元構造二次函數是求解本題的關鍵,考生需要熟悉基本原理,才可以在遇到生疏或繁難的問題,通過這些問題與基本問題的關系,“化生為熟,化繁為簡”解決問題.二次函數型恒成立問題的具體解決需要根據函數性質、圖像全面討論x2的系數、對稱軸、Δ值符號等解題.
一般地,二次函數型的恒成立問題有以下類型:
(1)類型1: 設 f(x)=ax2+bx+c(a/=0), f(x)>0(x∈R)恒成立 ?? a>0且Δ<0;
(2)類型2: 設f(x)=ax2+bx+c(a/=0)

策略三、逐段篩選法求解
5.(2016年四川高考卷理21題)設函數f(x)= ax2-a-lnx,其中a∈R.
(1)討論f(x)的單調性;


本題對a進行分類討論,逐段篩選出符合條件的a的范圍.求解的辦法是對函數(或構造的函數)求導,然后結合單調性等驗證不等式是否恒成立.這種解法既考查對不等式恒成立條件正面的探究過程,又考查不等式恒成立的否定過程,對考生能力要求高,命題者把其作為高考壓軸題的首選題型,活躍在高考試題中多年.其姐妹題為2016高考卷四川文第21題:
設函數f(x)=ax2-a-lnx,g(x)=其中a∈R,e=2.718···為自然對數的底數.
(1)討論f(x)的單調性
(2)證明: 當x>1時,g(x)>0.
(3)確定a的所有可能取值,使得f(x)>g(x)在區間(1,+∞)內恒成立.
相同類型的題目有:

(I)求函數f(x)的單調遞增區間;
(II)證明: 當x>1時,f(x)<x-1;
(III)確定實數k的所有可能取值,使得存在x0>1,當 x∈(1,x0)時,恒有f(x)>k(x-1).
3.(2015年福建高考卷理第20題)已知函數f(x)= ln(1+x),g(x)=kx(k∈R)
(I)證明: 當x>0時,f(x)<x;
(II)證明: 當k< 1時,存在 x0> 0,使得對任意x∈(0,x0),恒有f(x)>g(x);
(III)確定k的所有可能取值,使得存在t>0,對任意的x∈(0,t),恒有|f(x)-g(x)|<x2.
4.(15年新課標2理科21題)設函數f(x)=emx+x2-mx.
(1?)證明: f(x)在(-∞,0)單調遞減,在(0,+∞)單調遞增;
(II)若對于任意x1,x2∈[-1,1],都有|f(x1)-f(x2)|≤e-1,求m的取值范圍.
在解此類題目中,求解以逐段篩選法為主,輔之以構造函數、分離參變量等策略,用所學知識創造性地解決問題.同一類型的題目高頻率地作為高考壓軸題目出現,一方面說明這類題目有較好的區分度,另一方面也說明中學教學對此類問題研究不夠,這也要求再高三復習教學中要善于總結逐段篩選法的一般思維方式.
當然,含參恒成立問題的題型和解題策略遠不止這些,比如還有一次函數求解型,確定主元法,數形結合法,觀察、證明、猜想等方法.而在解題中,解題方法常是交叉使用的,且解法并不唯一.
恒成立問題對學生思維能力的要求遠遠高于對知識的理解與一般意義上的運用,它是一種用于檢測學生數學素質和思維能力的好載體,因此,含參恒成立問題深受命題者的青睞,它必將繼續成為今后數學高考的一個熱點,并且其命題背景還會更豐富.G·波利亞在《數學的發現》中曾說: “數學的技能比知識更重要.”因此,教師在復習過程中更要著重闡述分析問題和解決問題的一般規律和解題策略,從而讓復習更有效.
[1]朱永江.基于高中數學的恒成立問題分析[J].開封教育學院學報, 2015,(3): 230-231
[2]趙忠平.年年“題”不同歲歲“法”相似——高考全國卷不等式恒成立成立求參數范圍問題的解法分析[J].教學與管理,2012,(1): 72-73
[3]宋國清.談不等式恒成立問題的基本類型和常見解法[J].數學教研, 2013,(19): 42-43
[4]楊潔.新課標中函數恒成立問題的解法[J].凱里學院學報,2014, (12): 171-173

