“為遷移而教”
——以基本不等式教學設計為例*

華中師范大學數學與統計學學院 (430079) 王 靜華中師范大學教師教育學院 (430079) 胡典順

“為遷移而教”
——以基本不等式教學設計為例*

華中師范大學數學與統計學學院 (430079) 王 靜華中師范大學教師教育學院 (430079) 胡典順

一、引言

學習是一個連續的過程，任何學習都是學習者在已有知識經驗基礎上進行的，學習者原有的認知結構、知識經驗、技能和態度對新的學習產生影響，新知識的學習過程及結果又會對學習者原有的認知結構進行改組，對原有知識經驗進行擴充，對原有技能進行強化，這種新舊學習的相互影響就是學習的遷移，準確地說，一種學習對另一種學習的影響叫做學習遷移[1]．可見，遷移貫穿于學生的學習過程中，學生的學習離不開遷移．教師不可能將學生需要掌握的所有東西一一教給學生，很多的學習過程可以通過遷移來實現．學習者已經具有的經驗可能有助于順利解決當前的問題，也有可能會起阻礙作用，因此，在教學中，如何促進學生產生更多的正遷移、避免負遷移是教師值得深思的問題．

數學知識具有內在的邏輯性、系統性，教材編寫遵循循序漸進、螺旋上升的原則，前面學習的內容對后面的內容都有直接或間接的影響；高中階段的四大數學思想方法：數形結合、分類討論、函數與方程、轉化(化歸)以及換元法、數學歸納法、參數法、反證法等數學方法也都是在不同的知識內容中有相應的用法，學生如果掌握得好就會對后面的學習產生正遷移．除知識、思想、方法之外，技能、能力、情感、態度的學習同樣可以通過遷移實現．課堂教學是學生學、教師教的主陣地，把以上這些內容的遷移設置在課堂教學的各個環節中，是培養學生學習遷移能力的一種有效方式．在課題導入環節，要精心設計問題的情境，激發學生求知的興趣并創設學習的疑問；探究新知環節，使探究和遷移緊密聯系，深化對新知識的理解；在練習鞏固環節中，可以從與例題相似的題目入手，設置變式讓學生更好地掌握新知識，防止學生運用新知識時犯錯誤；在拓展延伸環節中，可以拓展學生的思維，有效地優化數學教學的效果，引導學生總結歸納、完善數學認知結構．

二、基本不等式教學設計

1．情境遷移，導入新課

(1)展示第24屆國際數學家大會的會標并介紹設計的相關背景(圖1)，引導學生找出這個會標中包含的幾何圖形，它的設計依據是趙爽弦圖(圖2)．

圖1 圖2 圖3

(2)利用幾何畫板改變弦圖中直角三角形的兩條直角邊邊長，展示變化過程，讓學生觀察、歸納出S大正方形≥4S直角三角形這個不等關系，即a2+b2≥2ab，引導學生分別從式子中和圖形中探究等號成立的條件．圖中a、b為直角三角形的邊長，因此是正實數，設置問題“對任意實數a、b，a2+b2≥2ab都成立嗎？”學生用配方法很快能完成證明．

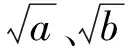
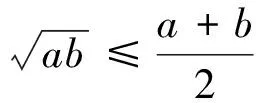
2．知識遷移，形成結論

(1)探究1：基本不等式的證明

讓學生自主探究，預設三種證明方法：作差法；分析法；綜合法．

(2)探究2：基本不等式的代數意義與幾何意義

(3)探究3：基本不等式鏈

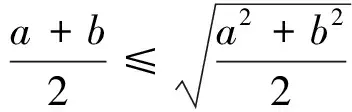
設計意圖：探究1引出基本不等式的概念及式子之后，引導學生對基本不等式進行自主證明、交流討論，讓學生在相互交流中掌握不同的證明方法．探究2從代數和幾何兩個方面探究基本不等式，“數”和“形”是數學學習的兩個重要對象，兩者的相互轉化可以為數學問題的研究提供廣闊的思路．借助圖形形象直觀地促進學生對基本不等式的代數理解，基本不等式的代數式則有助于更深入地理解其幾何意義，“數缺形時少直覺、形缺數時難入微”正是對“數”與“形”相互遷移的描述，兩者之間的這種正遷移能幫助學生更好地理解基本不等式．探究3的設置旨在讓學生掌握基本不等式鏈，揭示幾個不等式之間的聯系，優化學生關于不等式的數學認知結構，有利于學生在后面的學習中更好地實現數學知識的遷移．

3．習題遷移，深化認識

例2 (1)用籬笆圍一個面積為100m2的矩形菜園，問這個矩形的長、寬各為多少時，所用籬笆最短，最短的籬笆是多少？

(2)一段長為36m的籬笆圍成一個矩形菜園，問這個矩形的長、寬各為多少時，菜園的面積最大，最大面積是多少？

設計意圖：學習遷移現象在數學教學中廣泛存在，學習興趣、學習態度、學習方法、知識、技能、數學思想、能力等都是可以遷移的．習題的遷移也是常見的，我們常說的舉一反三、觸類旁通在數學解題中就是對習題遷移的描述．例1之后設置三個變式讓學生注意基本不等式使用的條件“一正二定三相等”，防止學生在運用基本不等式時忽略使用條件，避免負遷移的產生，盡可能地防止學生在后面的解題中犯錯誤．通過例2概括出基本不等式中“積定和最小、和定積最大”的規律，培養學生的概括能力．學生對已有知識的概括水平越高，就越能揭示同類知識的實質，把新知識納入已有的數學認知結構中，實現對新知識的同化或順應，從而發生正遷移．

4．能力遷移，發展思維

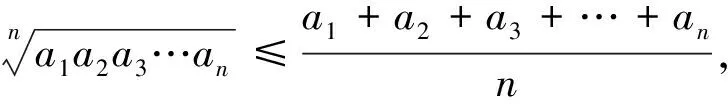
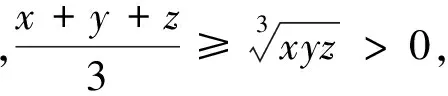
設計意圖：不等式是高中數學的重、難點，在基本不等式的教學中，讓學生了解與基本不等式相關的其他不等式有利于更好地掌握知識的內在結構，在數學教學中，教師應啟發學生掌握知識的內在結構的相互聯系．讓學生了解柯西不等式、重要不等式、基本不等式、均值不等式之間的關系，可以讓學生對不等式這個內容有更高層次的理解，從而優化學生對不等式的認知結構，在后面的學習中產生更多的正遷移．

三、結語

遷移的實質是概括，概括性越強遷移范圍就越廣；遷移的基礎是聯系，只有相互有聯系才能相互影響；遷移的實現是聯想，只有從問題聯想到已經掌握的知識技能，才能找到解決問題的策略[2]．因此，教師應該注重培養學生的概括能力，學生對已有的知識、經驗的概括水平越高，就越能把新知識納入已有的認知結構中，促進正遷移的產生．在數學教學中，教師應啟發學生找出那些具有高概括性、包攝性的基本概念和原理，掌握知識的內在結構的相互聯系，這樣既可以簡化知識，又可以靈活運用知識和產生新知識[3]．教師還應強調基礎知識和基本技能的獲得，因為要學習的新東西與學生已經掌握的基礎知識和基本技能之間存在聯系，只有掌握好基礎知識和基本技能，作為遷移的基礎的這種聯系才能促進正遷移．同時，基礎知識和基本技能還是實現聯想的基礎，沒有扎實的基本功，學生很難由問題聯想到認知結構中相關的知識、技能、方法等，問題就難以得到解決．遷移現象存在于課堂教學的各個環節，教師可以將各種遷移的策略、遷移理論融入進高中數學教學的過程中提高學生的學習遷移能力．教師無法代替學生習得遷移能力，需要做的是在課堂教學中為學生提供更好的遷移條件，精心設計好每一堂課，鼓勵學生發現問題、提出問題，為學生指明遷移的方向．

總之，作為教學活動的組織者、學生學習的促進者，教師要遵循“為遷移而教”的教學理念，創設高效率的課堂教學活動．讓課堂多一些有意義的學習，少一些機械的學習，在最近發展區中最大限度地促進學生知識、技能、情感、態度等方面的遷移，創造遷移氛圍、提高學生的學習遷移能力．

[1]喻 平.數學教育心理學[M].南寧：廣西教育出版社，2004.

[2]馬 波.遷移規律在中學數學教學中的運用[J].課程·教材·教法，2003(12)：29-32.

[3]朱華偉，張景中.論數學教學中的遷移[J].數學教育學報，2004，13(4)：17-19.

全國教育科學規劃教育部重點課題——TPACK視角下卓越教師培養的理論研究與實踐探索(課題編號DHA150287)．