小議二次函數(shù)綜合性問題突破視角

☉江蘇省常熟市滸浦高級中學(xué) 夏樸

小議二次函數(shù)綜合性問題突破視角

☉江蘇省常熟市滸浦高級中學(xué) 夏樸

眾所周知，高中數(shù)學(xué)函數(shù)問題最經(jīng)典的模型是以二次函數(shù)為背景設(shè)計的，二次函數(shù)既因為在生活生產(chǎn)實際中有著重要體現(xiàn)，也是中學(xué)生能夠解決的主要模型．通過二次函數(shù)可以研究函數(shù)的三要素、單調(diào)性、最值以及在問題解決過程中涉及的重要思想方法等．可以這么說，二次函數(shù)相關(guān)的綜合性問題一直是學(xué)生學(xué)習(xí)的難點．

從考試要求來看，“考試大綱”明確提出了理解二次函數(shù)的定義，掌握其圖像和性質(zhì)，以及理解和運用二次函數(shù)、一元二次方程、一元二次不等式之間的關(guān)系去解決相關(guān)問題，在問題解決過程中能夠運用思想方法將問題轉(zhuǎn)化為二次函數(shù)求解．從大綱要求來看，很明顯提出了二次函數(shù)學(xué)習(xí)的三個層次，其一是掌握基本知識和基本性質(zhì)，這是大部分學(xué)生普遍掌握的；其二是能運用整合性的知識聯(lián)系解決相關(guān)問題，這就選拔出了能力較強的學(xué)生；最后是能運用思想方法將綜合性問題通過二次函數(shù)模型求解，體現(xiàn)了選拔最優(yōu)秀學(xué)生的意圖．近年來，二次函數(shù)以綜合性問題呈現(xiàn)在試卷中，以函數(shù)、不等式、方程的相互等價轉(zhuǎn)換成為命題的常規(guī)形態(tài)，以導(dǎo)數(shù)的介入、解析幾何中的滲透成為有效的結(jié)合點．從難度來說，二次函數(shù)的深入挖掘成為區(qū)分學(xué)生能力的重要考核手段，成為教師教學(xué)關(guān)注的重點．下文從綜合性問題舉例來說明，教學(xué)中應(yīng)該選擇的突破視角．

一、圖形的視角

“小題小做”一直是高考重要的命題原則，也就是說要利用更為直觀、特殊的方式去解決小題．筆者認(rèn)為，對于二次函數(shù)綜合性小題的解決，多利用圖形化的視角嘗試是首要的選擇，看一個例題：

分析：借助二次函數(shù)的圖像，我們不難發(fā)現(xiàn)：值域為定值，因此其定義域可以在一定范圍內(nèi)變化，這種變換通過圖形的視角顯露無遺（如圖1），借助圖形的對稱性可以得到兩者之間的關(guān)系如圖1所示．

解析：令y=3，即x2-2x=3，解得x1= 3，x2=-1．又x=1時，y=-1，因此當(dāng)a=-1時，1≤b≤3都可以，即線段AB；當(dāng)b=3時，-1≤a≤1都可以，即線段AD．

點評：小題小做最常用的手段是圖形化視角、特殊化視角，擁有這樣的思維狀態(tài)對于考試有極大的幫助．本題較為合理地借助圖形化視角，將圖形中自變量的變換顯示出來，厘清變量間的對應(yīng)關(guān)系．本題還可以對相關(guān)問題進行變換：如將其變式為求|a-b|的最大值或者最小值等等．

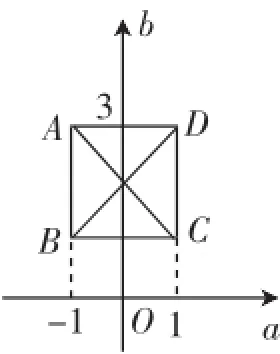
圖1

二、轉(zhuǎn)換主元的視角

二次函數(shù)含參變量問題是考查的難點之一，隨著參數(shù)的增多，學(xué)生對于問題的處理往往陷入混沌．在思考問題過程中，我們可以轉(zhuǎn)換研究主要元素的視角，讓問題呈現(xiàn)一種清晰的突破口．

問題2函數(shù)f（x）是定義在［-1，1］上的奇函數(shù)，且f（1）=1，若a，b∈［-1，1］，且a+b≠0時，恒有

（1）判斷并證明f（x）在［-1，1］上的單調(diào)性；

（2）若f（x）≤m2-2am+1對所有a∈［-1，1］恒成立，求m的取值范圍．

作為一名思想政治教育者,首先要克服首因效應(yīng)和近因效應(yīng)所造成的認(rèn)知偏見對教育者的影響，不能只憑第一印象或最新印象評價和判斷人，也不能輕信任何一種關(guān)于某人的信息，而應(yīng)當(dāng)用全面的、辯證的觀點看問題以及了解他人。教育者還可以充分利用首因效應(yīng)和近因效應(yīng)的積極作用,在教育內(nèi)容的選擇上利用二者提高教學(xué)效果。在與人相處時注意自己的儀容儀表、談吐等，給人留下良好的第一印象，作為教育者來說，開學(xué)第一課至關(guān)重要，準(zhǔn)備好開學(xué)第一課，給學(xué)生留下良好的印象。但更重要的是要有意識地引導(dǎo)教育對象用全面的觀點看問題。

分析：這是一個多元參量的典型問題．對于第（2）小問，我們不難發(fā)現(xiàn)學(xué)生難以清晰地辨解多個參量，不少學(xué)生無從下手．從問題的剖析來看，應(yīng)該是這樣嚴(yán)密的完整表述：“若f（x）≤m2-2am+1對任意的x∈［-1，1］，a∈［-1，1］都恒成立，求m的取值范圍．”因此首先研究哪個變量、進而研究哪個變量非常清晰，我們層層遞進來分析．由第（1）小問單調(diào)性可知，從變量x入手，即研究m2-2am+1≥f（x）max，這里可以說不費吹灰之力；在得到m2-2am≥0時思考哪個元素已經(jīng)告知？進一步研究哪個元素的問題？顯然變量a的范圍已經(jīng)告知，進一步研究變量m的取值范圍，因此轉(zhuǎn)換主元的視角躍然紙上，從而多個變量的問題也層層剝離，清晰求得．

解析：（1）略．

（2）因為f（x）≤m2-2am+1對所有x∈［-1，1］，a∈［-1，1］恒成立，即m2-2am+1≥f（x）max．

因為f（x）max=f（1）=1，所以m2-2am+1≥1，所以m2-2am≥0，即g（a）=-2am+m2≥0在［-1，1］上恒成立．

點評：轉(zhuǎn)換主要元素研究的視角是常見的二次函數(shù)綜合性問題選擇方法，通過元素主次位置的確定，將問題轉(zhuǎn)換為較為容易的函數(shù)模型，上述問題經(jīng)過轉(zhuǎn)換主元成為一次函數(shù)的研究，使得問題的解決變得容易很多．對于學(xué)生而言，轉(zhuǎn)換主元的視角是思考多元變量問題的恰當(dāng)手段，教學(xué)經(jīng)驗也告訴我們學(xué)生對于這種轉(zhuǎn)換尚不能合理接受，不少學(xué)生仍舊在二次函數(shù)的分類討論上大做文章，這種做法不可取，加強學(xué)生解題視角的引導(dǎo)成為關(guān)鍵．

三、變量分離的視角

對于二次函數(shù)綜合性問題來說，為了避免大量的分類討論，還可以從變量分離的視角入手思考問題．變量分離是綜合性問題的重要方法，即將研究的變量和參量進行合理的分離，這種分離最好是基于不用分類討論進行．變量分離的視角是很多問題的重要選擇方法，諸如恒成立問題、存在性問題、有解性問題等等．

（1）求m，n的值；

（2）當(dāng)x∈［1，+∞）時，判斷函數(shù)f（x）的單調(diào)性并證明；

分析：（1）略；（2）利用定義法或?qū)?shù)法加以證明；（3）中限制了字母參數(shù)的范圍的“三個二次”問題可以轉(zhuǎn)換變量來加以化解，而本題限制了自變量的范圍，一個比較簡潔的辦法就是分離變量，將含有自變量的放在一起，構(gòu)造一個新的函數(shù)然后再研究新函數(shù)的最值．

解：（1）（2）略．

（3）由題可知，2x2-2x+1＞2a（x-1）在x∈（2，4）上恒成

點評：為什么會想到利用參變分離的視角？這是教學(xué)需要向?qū)W生闡述的關(guān)鍵．考慮到變量x∈（2，4），顯然在分離過程中不需要對其進行討論，自然分離成為了解決問題的首選方式．此類問題單刀直入，緊抓最終的目標(biāo)，先簡化等式或不等式的一邊，然后利用函數(shù)的性質(zhì)研究新函數(shù)的最值．此法也可以推廣到次數(shù)更高的問題．學(xué)生面對這類題型的最大問題：一方面在較復(fù)雜的問題情境中很難將目標(biāo)字母理清楚，另一方面對于除過去的式子2（x-1）的分析，如果x∈（0，4），使得式子2（x-1）有正有負也有0，就要進行分類討論，更要關(guān)注不等號的方向．學(xué)生常見的錯誤就是對不等式的兩邊分開討論，但問題是兩邊不在同一處取得最值．當(dāng)然此題也可以用分類討論方法解決．

四、凹凸性的視角

函數(shù)凹凸性是高等數(shù)學(xué)必備的學(xué)識之一，但在中學(xué)數(shù)學(xué)中對于凹凸性的認(rèn)識并不深刻，也沒有特別的相關(guān)概念介紹．在導(dǎo)數(shù)相關(guān)知識中，對于函數(shù)研究過程中能利用凹凸性視角，大大簡化了問題的求解過程．

問題4已知函數(shù)f（x）=ax2+bx+c（a≠0）的圖像過（-1，0）點，則存在常數(shù)a，b，c，使不等式對一切實數(shù)恒成立．

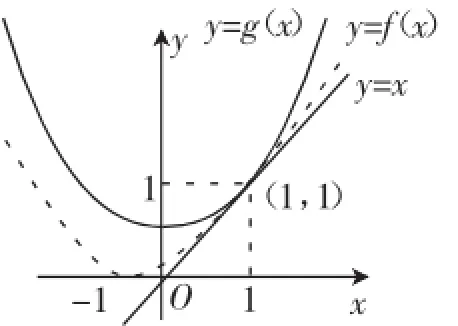
圖2

點評：本題恒成立的求解另辟蹊徑，從兩邊夾f（1）= 1入手，思考恒成立后續(xù)問題的處理，通過思考即可發(fā)現(xiàn)只要找到直線與拋物線、拋物線與拋物線相切位置即可知道，其余點處恒成立．思考拋物線凹凸性可知，尋找切點必定出于兩邊夾的特殊值位置，即f（1）=1處，這說明函數(shù)凹凸性的理解大大簡化了一般學(xué)生利用判別式法求解的過程，體現(xiàn)出了思維的含量、突破的新視角，可見對于上凸或下凸函數(shù)等有深刻的認(rèn)知、提前的預(yù)判量，大大提高了問題解決的可能性，是引導(dǎo)優(yōu)秀學(xué)生思維的新視角．

總之，二次函數(shù)綜合性問題的處理是一個漸學(xué)漸長的過程．從本文所舉的四個案例來看，對小題和多元變量的處理，靈活掌握知識、合理選擇使用是綜合二次函數(shù)問題的常見方法和技能，是突破的常見視角．上述問題也能從其他視角入手，有興趣的讀者也可以一試，對比文中所選視角，可能會有意想不到的收獲．

1.柴賢亭.函數(shù)教學(xué)中的思維啟發(fā)設(shè)計［J］.教學(xué)與管理，2013（8）.

2.鄭毓信.解題教學(xué)理論在二次函數(shù)中的實踐［J］.中學(xué)數(shù)學(xué)月刊，2015（1）.