群體自助年金化的給付模型及逆選擇風險研究
張 琳,楊起軍
(湖南大學 金融與統計學院,湖南 長沙 410079)*
·金融與保險·
群體自助年金化的給付模型及逆選擇風險研究
張 琳,楊起軍
(湖南大學 金融與統計學院,湖南 長沙 410079)*
基于已有的研究成果,通過改進年金精算現值的計算方式,推導出更為合理的群體自助年金化給付遞推模型;隨后,以成員的資金分配額度及其主觀意愿的生存率的一階偏導數來刻畫逆選擇風險,比較了群體自助年金化和普通養老年金的逆選擇風險的大小。
群體自助年金化;長壽風險;確定等值法
一、引言
我國已步入老齡社會,隨著老年人口的增加以及壽命的不斷延長,長壽風險對我國國計民生的影響愈發顯著,需要一種合適的方法來實現其有效轉移。根據承擔主體的差異,長壽風險可以分為個體長壽風險和聚合長壽風險。個體長壽風險與一般的保險風險并無本質區別,但是聚合長壽風險無法通過大數法則來進行分散,只能通過各種渠道來尋找分擔主體。保險行業不愿承擔聚合長壽風險,而年金成員不愿承擔個體長壽風險,不妨將二者的作用互換,由此提出的年金池承擔個體長壽風險而成員承擔聚合長壽風險的養老年金模式即為群體自助年金化。
群體自助年金化又叫互助養老年金(PooledAnnuityFund),JohnPiggott,etal.(2005)最早提出了較為完整的概念,并推導了精算公平原則下的給付遞推公式[1]。但是他們并未對群體自助年金化的特點進行很好的概括,且其推導出的給付遞推模型不夠完善。隨后,RalphGoldsticker(2007)給出了群體自助年金化的定性分析,詳細闡述了其概念及特點[2]。
在JohnPiggott等人和RalphGoldsticker的研究基礎上,關于群體自助年金化的后續研究內容主要集中在以下幾個方面:(1)JonathanBarryForman(2014)從企業人員規模的角度研究了群體自助年金化的適用范圍[3]。(2)MosheA.etal.(2015)通過求解歐拉--拉格朗日方程得到基于終生效用最大化的群體自助年金化的結構,并檢驗了該結構關于年金人數和逆選擇風險的敏感程度[4]。(3)MichaelZ.Stamos(2008)將群體自助年金化和普通養老年金結合在一起,并通過HJB方程分析了不同情況下二者的最優組合[5]。(4)CatherineDonnelly,etal.(2013)同樣基于終生效用最大化理論,將群體自助年金化和死亡率連接基金做了對比,最后發現:當投資收益率的方差波動較小時,群體自助年金化的期望效用大于死亡率連接基金[6]。本文在JohnPiggott等人的研究基礎上,通過改進其推導過程得到更為貼近實際情況的群體自助年金化給付遞推模型;隨后,根據RalphGoldsticker提出的群體自助年金化的特點,從逆選擇的角度驗證了相對于普通養老年金的群體自助年金化逆選擇風險更小的假設。
二、群體自助年金化的給付模型
根據JohnPiggott等人以及RalphGoldsticker(2007)的研究成果可知,群體自助年金化可以為其成員提供類似于普通養老年金的現金流,而發起人無需承擔聚合長壽風險。
具體而言,群體自助年金化和普通的養老年金之間的兩個主要區別為:(1)由于具有互助性質,如果群體自助年金化中的某個成員死亡,他的資金將會按照一定的方式在年金池內進行再分配,這部分待分配的資金被稱為死亡率信用(MortalityCredit)。(2)每年會根據最新的信息來預測未來死亡率的分布和利率的波動,根據預測得到的結果計算給付額調整因子,用調整因子去修正下一年度的給付額。
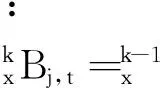
(1)
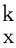
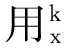
(2)
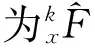
(4)
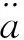
(5)
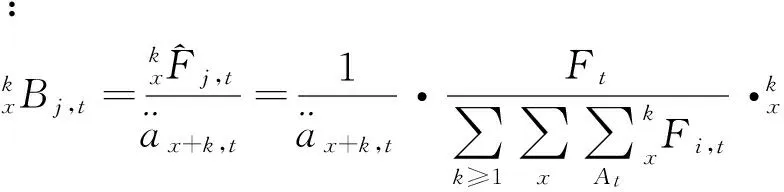
(6)
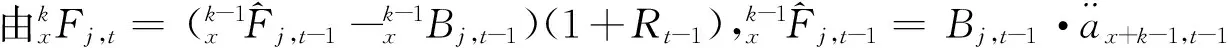
(7)
在此情形下,t時刻死亡率調整因子為:
(8)
t時刻的利率調整因子為:
(9)
由此,得到群體自助年金化的更為合理的給付遞推模型。群體自助年金化相對于普通養老年金而言具有較高的期望給付額,原因有兩點:首先,由于群體自助年金化是由成員承擔聚合長壽風險和投資風險,因而成員不需要支付將這部分風險轉移給保險公司而產生風險保費;其次,通過給付遞推模型的推導過程可以看出:計算群體自助年金化給付額時,死亡率精算假設是基于平均余命,小于普通養老年金所基于的生命表中的極限生存年齡。
三、群體自助年金化的逆選擇風險
Ralph Goldsticker曾提出:在群體自助年金化模式下,由于聚合長壽風險的承擔者已經由年金池變成了年金成員,對發起人而言,群體自助年金化的逆選擇風險顯然較小[2]。但是Ralph Goldsticker只是給出了定性的分析,并沒有具體的假設證明。從前面的推導過程來看,群體自助年金化的給付模式和普通養老年金相比最大的區別在于每年增加了一個調整因子DEAt·IEAt,而該調整因子可以看作是一個有約束條件的隨機變量。因此,以下將通過假設和證明,來比較群體自助年金化和普通養老年金的逆選擇風險的大小。
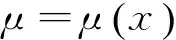
(10)
W0=A-a-g
(11)
W1=Raa+RggY
(12)
其中,v表示折現因子,p表示根據Q的主觀意愿確定的生存概率,給付調整因子DEAt·IEAt簡記為Y。
對Q的效用函數求期望效用:
(13)
假設Q為理性人,即他會選擇使得自己的期望效用最大化的財富分配方式。因此,對其期望效用求偏微分:
(14)
(15)
(16)
(17)
比較式(16)(17)得:
(18)
即當a和g同時滿足公式(16)(17)時,Q的期望效用最大。
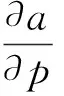
公式(16)(17)兩邊均對p求偏導可得:
(19)
(20)
比較式(19)(20),且根據式(18)可化簡得:
(21)
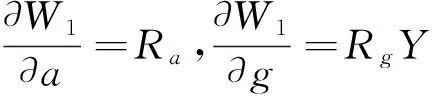
(22)
(23)
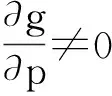
(24)
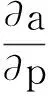
vp(u″(W0)E(u″(W1)(Ra-RgY)2)+
(E(u″(W1)Y))2))=|H|
其中:
H表示期望效用對a和g的二階偏導數的黑塞矩陣。記:
—v2pRaE(u′(W1))=W,RgE(u″(W1)Y(RgY-Ra))=A,RaE(u″(W1)(Ra-RgY))=B
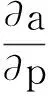
(25)
(26)
因此,在Q作出投資決策的時候,以確定等值法為基本原則:即包含不同風險類型或不同風險水平的現金流的效用相等,即:
(27)
根據風險厭惡型消費者效用函數的凹凸性可知:
又由效用函數的遞增性可知:
Ra 在此條件下,提出假設1和假設2并予以證明。 首先,很顯然W=—v2pRaE(u′(W1))<0;其次,A+B=RgE(u″(W1)Y(RgY-Ra))+RaE(u″(W1)(Ra-RgY))=E(μ″(W1)(Ra+(RgY))2)<0;最后,根據黑塞矩陣副半正定的性質可知:|H|>0。 根據公式(24),即證 根據E(μ″(W1)Y2)≤E(μ″(W1))(E(Y))2可知: (28) 式(28)等價于RgE(u″(W1)Y2) (29) (30) 從而假設2成立,即對發起人而言,群體自助年金化成員的逆選擇風險比普通養老年金模式要小。 之所以假設E(μ″(W1)Y2)≤E(μ″(W1))(EY)2,是因為長壽風險對死亡率的影響是一個較為緩慢而且漸變的過程,即E(Y)接近1但是小于1,因此,以E(μ″(W1)Y2)≤E(μ″(W1))(EY)2的形式給E(Y)設定一個上限。從而不難證明,如果投資者的效用函數是CRRA效用函數或是指數效用函數時,該不等式均成立。 群體自助年金化為我國政府、企業及保險行業等提供了解決長壽風險的新思路。以上通過改進年金精算現值的計算得到了更為合理的給付遞推模型,并證明了和普通養老年金相比的群體自助年金化具有逆選擇風險較小的優勢。后續的研究工作可以從如下三個角度入手:(1)基于我國國情對群體自助年金化的可行性進行分析,闡明其市場前景、挑戰及需要改進的地方;(2)關于規范群體自助年金化經營的法律法規建設方面提出相應的建議;(3)從給付額、替代率、長壽風險分擔比例等方面入手,通過建立恰當的模型來對比分析群體自助年金化和普通養老年金的區別和各自的優劣勢。 [1]JohnPiggott,EmilianoA.Valdez,BettinaDetzel.Thesimpleanalyticsofapooledannuityfund[J].TheJournalofRiskandInsurance, 2005, 72: 497-520. [2]RalphGoldsticker.Amutualfundtoyieldannuity-likebenefits[J].FinancialAnalystsJourna, 2007, 63: 63-67. [3]JonathanBarryForman.Tontinepensions:asolutiontothestateandlocalpensionunderfundingcrisis[J].UniversityofOklahomaCollegeofLaw, 2014, 15: 86-89. [4]MosheA,Milevsky,ThomasS.Salisbury.Optimalretirementincometontines[J].Insurance:MathematicsandEconomics, 2015, 64: 91-105. [5]MichaelZ.Stamos.Optimalconsumptionandportfoliochoiceforpooledannuityfunds[J].Insurance:MathematicsandEconomics, 2008, 43: 56-68. [6]CatherineDonnelly,MontserratGuillén,JensPerchNielsen.Exchanginguncertainmortalityforacost[J].Insurance:MathematicsandEconomics, 2013, 52: 65-76. (責任編輯:墨 彥) The Study of The Payment Model and Adverse Selection Risk of Group Self -Annuitisation ZHANG Lin,YANG Qijun (CollegeofFinanceandStatistics,HunanUniversity,Changsha,Hunan410079,China) On the basis of the research before, by improving the calculation mode of actuarial present value of the annuity, this article deduces a more reasonable payment model; then contrast the value of adverse selection risk of ordinary pensions and the group self -annuitisation, which is mearsured by the first order partial derivative of capital allocation of the menbers to the survival rate based on subjective intension of the menbers. Group Self -Annuitisation; Longevity Risk; Certainty Equivalent Method 2016 -11 -12; 2017 -01 -02 張 琳(1963—),女,湖北漢陽人,湖南大學金融與統計學院教授,研究方向:精算理論的實務。 F842.6 A 1003 -7217(2017)02 -0037 -05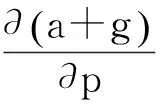
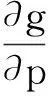
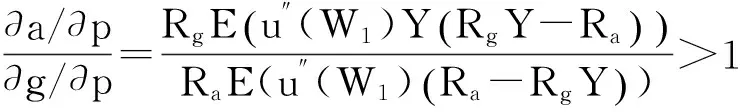
四、結 論

