別樣活動巧設計 此處無痕勝有痕
——強震球老師《圓的認識》一課教學賞析

趙　潔

無痕教育，是指“把教育意圖和目的隱藏起來，通過間接、暗示或迂回的方式，給學生以教育的一種教育方式。”在數學課堂上，如果巧妙地設計活動，把教學的目標隱藏在數學活動中，讓學生在活動過程中充分地進行觀察、比較、動手操作等親身體驗，在活動反饋中充分地表達、質疑和討論，這正是利用數學活動進行無痕教育的手段。實踐證明，這樣可以使學生獲得對數學知識技能的深入理解。

以下通過介紹強震球老師在《圓的認識》一課中所設計的三個數學活動，分析如何利用數學活動來實現無痕教育。

【案例片斷】

活動一：用圓規畫圓。

?

【案例賞析】

在畫圓活動的過程中，強老師并沒有給出任何指導。強老師認為，在每一節數學課開始之前，學生必定對所學的知識有他自己獨特的理解，或者有他自己的學習經驗。實踐證明，雖然之前沒有學習過用圓規畫圓，但許多學生都已經有過用圓規畫圓的認識和經驗。所以，如果這時仍然堅持教師帶領學生去畫的教法，那么必然有些學生認為自己已經會畫了而不認真聽講。反之，放手讓學生去畫，學生雖然會畫但是在反饋階段會立刻發現自己畫圓過程中存在的各種問題。此時再用視頻播放用圓規畫圓的標準方法，使得學生帶著問題去學習，提高了學習效率。這時再要求學生重新畫一個圓，學生就有機會改正自己存在的問題。

【案例片斷】

活動二：用繩作為工具畫圓。

?

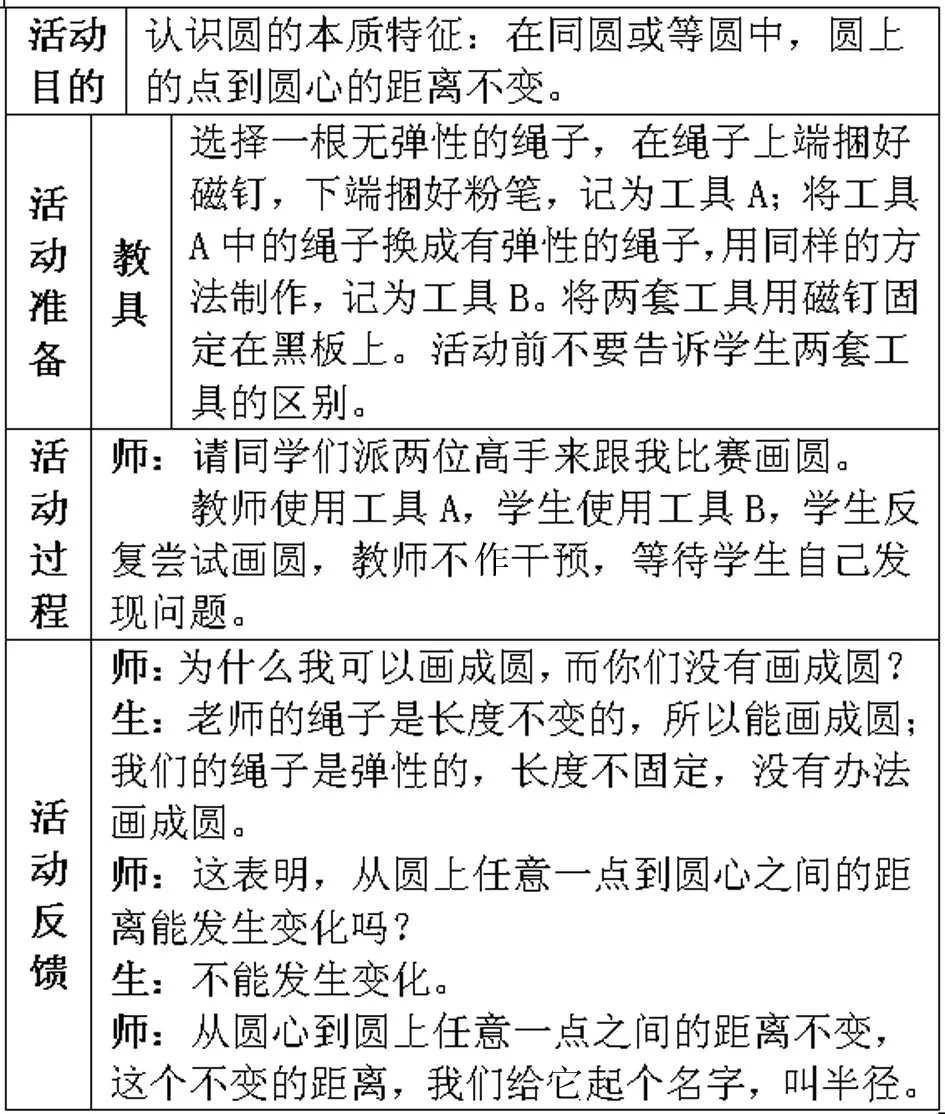
【案例賞析】

在活動之初，強老師沒有告訴學生兩種工具的區別，這為學生探索圓的本質特征埋下伏筆。試想，如果強老師在開始就把活動的目的和兩種工具的區別告訴大家，那么學生就不會對畫圓過程有強烈的體驗，自然也就不會對圓的本質特征產生深刻的印象。

與第一個數學活動相比較，看起來同樣是畫圓，那為什么要進行兩個類似的活動呢？究其目的，第一個活動的目的是要求學生學會畫圓的方法，而第二個活動的目的則是要探究圓的本質特征。強老師巧妙地在活動之初將活動目的先隱藏起來，再通過活動過程和活動反饋將目的層層剝開，讓學生恍然大悟。同時，半徑概念的必要性也通過這個活動充分地顯現出來。

【案例片斷】

活動三：給自行車輪胎裝鋼絲。

?

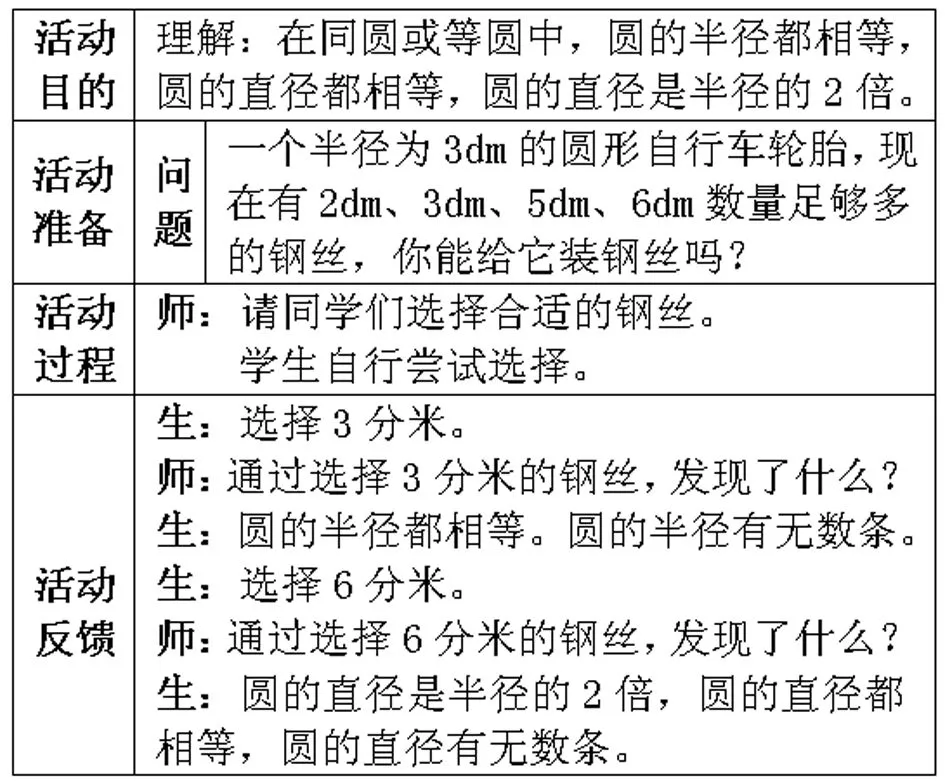
【案例賞析】

與通常的《圓的認識》教學不同，強老師沒有用“畫一畫、量一量、比一比”小組合作討論的形式，而是利用了生活中的常見圓形模型——自行車車輪。將自行車車輪用于這個活動中有兩點巧妙之處：第一，車輪是圓形的；第二，車輪的鋼絲通常是從車軸出發到達車輪邊緣上的，也就是一個端點在圓心、另一個端點在圓上的，所以可以用到圓的半徑或直徑。學生雖然對圓的半徑和直徑并不了解，但他們對自行車車輪非常熟悉。通過選擇鋼絲長度的活動，自然而然地就會將生活中的經驗上升為對數學的認識，于是很容易就能理解“在同圓或等圓中，圓的半徑都相等，圓的直徑都相等，圓的直徑是半徑的兩倍。”比起“畫一畫、量一量、比一比”的教學方法，輕松地避開了測量誤差的問題。

【感悟思考】

強老師巧妙地進行活動課設計，真正實現了“不知不覺中開始、潛移默化中理解、循序漸進中掌握、春風化雨中提升”的無痕教育理念。

一、活動之初，隱藏目的

數學活動具有較強的內隱性。數學活動可以讓學生獲得基本活動經驗，而且能夠開啟數學思維活動，從而理解數學的本質。在活動之初，先把活動目的隱藏起來，再通過之后的活動過程和活動反饋逐步展現活動目的。最后活動目的完全展現出來，學生就會有靈機一動、大徹大悟的感覺。

二、活動過程，充分體驗

在活動過程中，教師不作任何干預，而是給學生充分體驗的時間，通過觀察、比較、動手操作等方式進行自由探索。即使學生在體驗的過程中出現認知或操作的錯誤，也無需立刻指出，而是可以到之后的活動反饋中再發現問題，改正問題。正是因為有了活動過程中的體驗或失誤，學生才會對所要學習的數學對象有著更深刻的認識。

三、活動反饋，充分表達

活動反饋是數學活動中的重要環節。在活動過程結束后，應當根據活動結果，剝離背景的實際意義，回歸到數學中，得出數學結論。此時，教師的角色會退為組織者、合作者、引導者。通過對活動過程的匯報討論，充分表達自己的想法或困惑，學生可以強化自己的正確認識、糾正自己的錯誤認識，同時獲得對數學本質的充分理解。

從整節課的角度來看，數學活動的設計應當圍繞教學目標環環相扣，層次遞進，逐步深入，使得學生在親身體驗中不知不覺地認識數學的本質，真正做到“別樣活動巧設計，此處無痕勝有痕”。