巧用幾何直觀突破教學難點

趙海英

《數學課程標準》指出：“借助幾何直觀可以把復雜的數學問題變得簡明、形象，有助于探索解決問題的思路，預測結果。幾何直觀可以幫助學生直觀地理解數學，在整個數學學習過程中發揮著重要作用。”在課堂教學中，我們如果能根據幾何直觀的特點，巧妙運用，那么在突破教學難點方面，將會起到意想不到的效果。

一、巧用直觀圖形，理解運算定律

四年級《乘法分配律》這節課的教學情境，教材呈現的是長方形的墻面（如下圖所示），求貼了多少塊瓷磚。

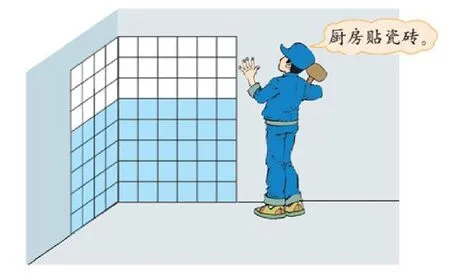
通過這幅圖，學生很快發現有多種算法：可以按照每行有10塊瓷磚，藍色的有5行，白色的有3行，然后求藍色和白色一共有多少塊。也可以白色和藍色混在一起，每列有8塊，左邊的墻有4列，右邊的墻有6列。根據以上的分析可以列式為：

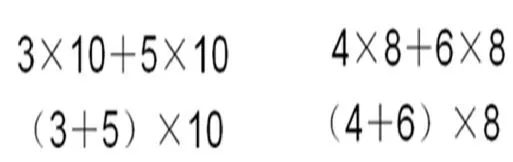
學生通過算式及結果的對比，以及對于直觀圖形的觀察就很容易理解乘法分配律的算理了。否則，僅僅通過計算以及算式的特點理解起來就沒有那么到位了。在這一節課的內容編排中，為了更深層次地理解乘法分配律的算理，教材中在“練一練”的練習題里也有一道通過圖形來說明為什么等式成立的練習題：

結合圖與同伴說說等式3×6＋4×3＝（6＋4）×3 為什么成立。

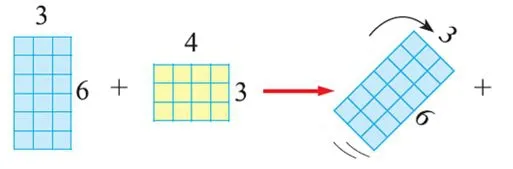
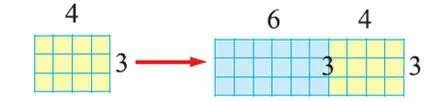
這樣的編排設計，遵循了由直觀到抽象的過程，便于學生理解乘法分配律的原理，發揮了數形結合的優點，體現了直觀幾何在學習中的恰當運用。

二、巧用直觀圖形，理解小數乘法計算法則

四年級《小數乘法》中有這樣的學習內容：

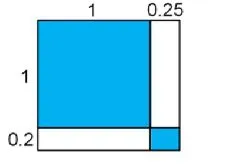
這個學習內容是在學生學習了小數的豎式乘法以后，教材編寫者為了更深入地理解小數乘法的算理而設計的一個問題。對于1.2×1.25能否可以用 1×1＋0.2×0.25來計算？如果只是讓學生通過計算“1.2×1.25 和 1×1＋0.2×0.25”來說明，學生只是知其然而不知其所以然。但是教材設計了上面右圖這一直觀圖形，就能很形象地幫助學生理解為什么不能用1×1＋0.2×0.25來進行計算。從圖中很容易看出要計算1.2×1.25的結果，應包含四個部分的面積，這四個部分的總面積才是1.2×1.25的積，而不是僅僅算出藍色的兩部分的面積之和。這對于學生理解算理很有幫助，北師大版教材對于這種類似的幾何直觀的設計很多，既體現了數形結合又體現幾何和代數的融合性，既解釋了小數乘小數的計算原理，又為初中的多項式乘法打下了基礎。這樣的設計，充分體現了《數學課程標準》中的課程基本理念“要重視直觀，處理好直觀與抽象的關系”。

三、運用直觀操作，理解分數乘法算理

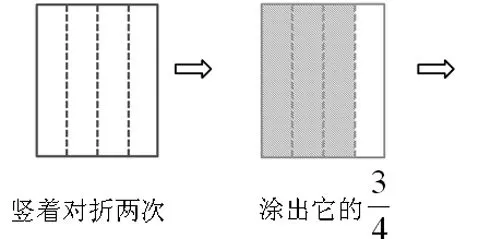
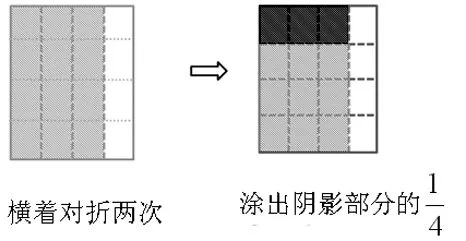
這樣的設計簡直太妙了。如果沒有運用圖形，就按照分數乘法的意義表示求的是多少？就是把平均分成4份，取其中的一份是多少？這樣確實也能推出這個算式的結果，但學生理解起來有些抽象。所以這里先讓學生折一折，然后再想一想、算一算。在動手操作的過程中找到解決問題的方法，就很容易看出的結果是，然后再來觀察積的分子和分母與兩個乘數的分子和分母之間的關系，從而歸納出分數乘分數的計算方法。這樣的設計充分體現了《數學課程標準》中關于課程設計思路的要求：“在呈現作為知識與技能的數學結果的同時，重視學生已有的經驗，使學生體驗從實際背景中抽象出數學問題、構建數學模型、尋求結果、解決問題的過程”，也就是我們平時說的除了重視知識的結論，我們更要重視知識的形成過程，既要知其然，更要知其所以然。

四、巧用幾何直觀，解決實際問題

1.巧用直觀圖形，理解數學概念。

四年級《小數點搬家》的學習內容，教材是這樣編排的：

小數點向左移動，小數的大小發生了什么變化？說一說，填一填。

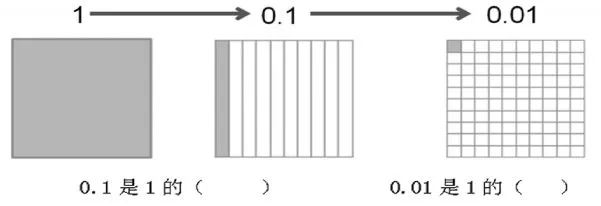
小數點搬家引起小數大小的變化本來是很抽象的一個教學內容，是教學的難點，學生很難理解，但是用圖形來表示各個數，再來觀察這幾個數之間的關系就比較容易了，通過直觀找到結果，然后再抽象出結論，小數點向左移動一位，得到的數是它的小數點向左移動兩位，得到的數是它的

類似地在計數單位的學習上都運用了幾何圖形的形式來說明“滿十進一”的十進制關系，不論是整數還是小數，這樣的設計讓本來很抽象的十進制通過直觀地再現，學生就很容易理解了。

2.巧用直觀圖形，解決數學問題。

四年級下冊第12頁有一道這樣的練習題：

同學們進行跳遠比賽。冬冬跳了3.16米，亮亮比冬冬多跳了0.23米，強強比亮亮少跳0.12米，強強跳了多少米？請把下圖補充完整再計算。

下圖是補充完整的圖：

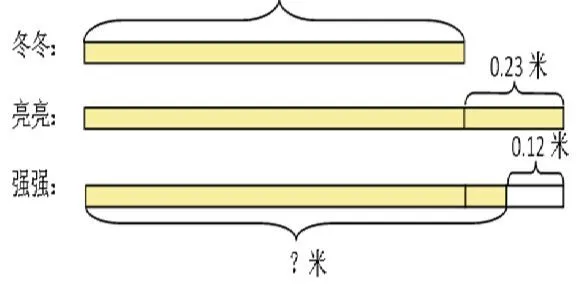
這道題目把三個人的跳遠成績做了對比，數量關系稍微復雜些，對于理清這三個量的關系，教材編者采取了讓學生先把圖補充完整，然后再計算。就是利用直觀圖形，幫助學生理清較復雜的數量關系，從而解決這一數學問題。

方法一：先求亮亮的跳遠成績：3.16+0.23=3.39（米）。

再求強強的成績：3.39-0.12=3.27（米）。

方法二：先求強強比冬冬多跳了0.23-0.12=0.11（米）。

再求強強的跳遠成績：3.16+0.11=3.27（米）。

這一題如果沒有運用直觀圖形，學生很難發現第二種方法。可見幾何直觀圖的編排與運用是何等的重要。

其實，這種編排在北師大版教材中隨處可見，在后續學習的行程問題、分數應用題、長方體的表面積及體積等方面，幾何直觀圖都是一個很重要的解題策略和解題方法。我們要善于發現和總結，引領學生充分利用幾何直觀的優勢，突破教學難點，提高教學效率，進一步培養學生運用不同策略解答問題的思維方式，發展學生的應用意識和創新意識。