《除數是整數的小數除法》教學片斷與反思

朱學堯

【片斷1】嘗試計算，在比對中初步感知

師：出示例4，提出問題：每千克蘋果多少元？

生：9.6÷3=

師：估一估大約是多少元

師：自己試著再算一算，把你的想法記錄在作業紙上。

教師巡視中發現學生的思路，選擇有代表性的想法進行交流：

方法1：把9.6元轉化成96角，用96除以3等于32角，32角=3元2角=3.2元。

方法2：把9.6元轉化成96角，用96除以3等于32角，然后根據商不變性質，直接把32角寫出3.2元。

方法 3:9÷3=3（元），6÷3=2（角）。3元+2角=3元2角=3.2元。

師：同學們能把新的知識轉化成舊知識來解決是一種很好的學習方法。還有的同學是用豎式方法來計算的，我想請他們說說每一步表示什么意思？（先展示兩種正確的豎式方法）

豎式1：

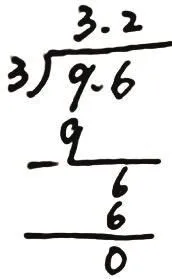
師：這么好的方法，誰來指導老師進行板書？（學生一邊說計算過程，教師一邊板書豎式）豎式中的6表示什么意思？是怎么得到的？

生：6表示6個0.1，是把十分位上的6拉下來的

師：想一想這樣做有沒有道理，對于這種方法有什么想說的？

生：為什么要寫成6，而不寫成0.6？

師：你的意思是這樣寫嗎？

豎式2：

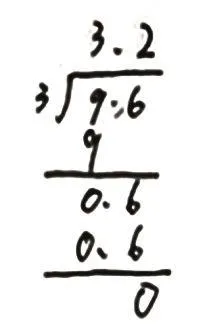
師：第二次分的到底是6還是0.6呢？先來回憶一下這個6表示什么意思，它是怎么組成的？如果用我們熟悉的數的組成或借助于元、角、分之間的關系如何來解釋？

生：這里的6表示6個0.1，也就是6角不是6元。

生：因為0.6元不能直接平均分成3份，把0.6元轉化成6角來平均分成3份，一份就是2角，也就是0.2元。

師：那像上面那樣，豎式下面寫0.6可以嗎？

生：行，寫0.6就表示0個1和6個十分之一，結果還是6個十分之一。

（教師相機在豎式1中6的旁邊板書：“……6個十分之一”）

生：如果寫0.6，就表示0.6個1，0.6個1平均分成3份，一份是0.2個1，2還是要寫在十分位上。

師：2要寫在哪一位上？怎么才能確定2在十分位上呢？

生：2要寫在十分位上，為了確定商的十分位的位置要先點上小數點，再寫2，2才能表示 2個 0.1。

（教師相機在豎式1中，商2的旁邊板書：“……2個十分之一”）

師：看來，小數點的作用還真不小，它是區分個位和十分位的重要標志。

師：如果把除數3改成2，下面橫線下面該寫什么？

生：寫1，然后把6拉下來，變成16。

師：這里的16表示什么意思？

生：1表示1個一，也就是10個0.1，與0.6合起來表示16個0.1，16個0.1除以2，是8個0.1，因此，商的十分位就是8。

教師引導學生尋找口算與豎式之間的關聯點，打通口算、整數與小數除法間的聯系。

師：再呈現幾個錯誤的豎式，請同學辨析。

豎式3：

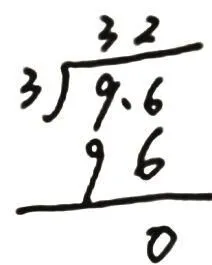
豎式4：

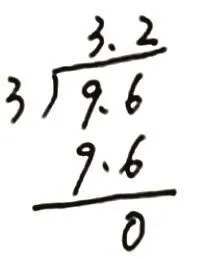
生：豎式 3，3×32是 96了，而被除數是9.6，而且，估算時，每千克蘋果大約3塊多錢，因此商是3.2而不是32,乘的積96應改成9.6。

生：豎式4，應先用整數部分的9來除以3，再用小數部分的6來除以3，不能一下子寫下來。

【反思：9.6÷3，與學生已有的整數除法聯系比較緊密，學生可以利用元、角、分之間的關系，把9.6元轉化成低級單位，變成96角，然后按照整數除法的方法來進行口算或豎式計算，最后利用商不變的性質，把商再縮小10倍，得到9.6÷3的商。學生基本上都能口算得到正確的商。讓學生嘗試豎式計算，并且在反饋環節，先呈現兩個正確的豎式，旨在給學生一個正確的豎式表象，然后，利用元、角、分之間的關系以及整數與小數的位置關系來解釋算理。在比對的辨析中，讓學生運用正確的表象來分析錯誤的算法，“清者更清，濁者更濁”，同時，為了便于學生體會到整數與小數除法的本質含義是一樣的，都是把計數單位進行平均分，當較大的計數單位不夠再分時，要化成比它更小的下一級的計數單位接著再分，不同之處在于小數除法計算中，需要把幾個一轉化成若干個十分之一的考慮。我們把除數3改成2，其目的是讓學生理解余下來的1平均分成2份，不夠商1，怎么辦？這一經驗積累，為解決下面兩個問題奠定基礎。而商的小數點，在什么時候點？我們順應學生的分析，“為了確定商的十分位的位置，要先點上小數點，再寫2”，這樣商的小數點的產生就不突兀了。】

【片斷2】運用經驗，深化算法

師：你們能嘗試解決“每千克香蕉多少元”和“每千克橘子多少元”這兩個問題嗎？有疑問可以在小組內交流。

生：12÷5=5.7÷6=

匯報交流，教師選擇有代表性方法進行交流。

教師出示以下幾種算法，交流哪一種算法是正確的（不正確的），說明其中的算理。

豎式5：

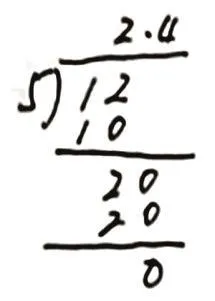
豎式6：

豎式7：

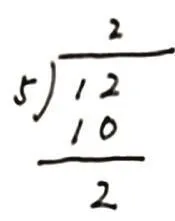
豎式8：

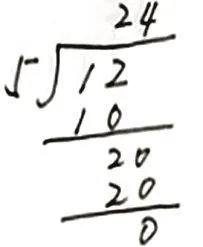
生：第5個和第6個豎式是正確的，12除以5商2，余2元，不夠商1元，把2元看成20角，20角除以5是4角。因此商是2元4角，也就是2.4元。

師：第6個豎式余數2后面補0是什么意思？

生：表示把2元換成20角。

師：既然豎式5和豎式6計算都正確，那它們之間有什么相同點和不同點嗎？豎式6下面的2.0可以寫成20嗎？

生：豎式6中的12后面點點補0，是把整數改成小數，這樣便于確定商的小數點在哪里，下面2.0可以寫成20，因為2.0表示2個1，除以5不夠商1，還是需要把2.0看成20個0.1來除以5的。

生：豎式5中的12后面雖然沒有補0，但我們可以認為12的后面有許多0。因為任何一個整數后面都可以點上小數點再補0。

師：這兩個同學都從另一個層面強調了12后面的小數點“隱藏”在哪里，這樣商的小數點就不容易漏了。

師：你覺得哪一個豎式的書寫比較簡單？

生：第5個豎式。

師：請同學辨析兩個錯誤的豎式。

生：豎式7，把余數2元，換成20角，還可以繼續除下去。

生：豎式 8，商 24，漏了點小數點，商的結果不可能是這么大的。

師：那怎樣防止商漏點小數點呢？

生：可以在12后面先點上小數點。

生：商2以后，要先點上小數點再往下除。

師：請同學們集體回答5.7÷6=？

交流時，突出商的整數部分為什么要補0；第一次乘的積54，不要寫成5.4；余下來的3后面添0后要繼續往下除三個問題。

教師結合黑板上的“三個”豎式，引導學生討論：商的小數點與被除數的小數點位置關系；哪一步計算是與整數除法相同的或不同的；計算小數除法要注意什么。

【反思：在處理12÷5的豎式時，由于學生在解決第一個問題時，已經積累了把“幾個1轉化成多少個0.1”的經驗，在此處，重點讓學生體會到被除數是整數，可以看成一個特殊的小數，讓被除數“隱藏”的小數點顯露出來，為確定商的小數點提供依據。而在處理5.7÷6時，僅讓學生集體交流商的整數部分為什么要補0；第一次乘的積是寫54還是5.4；余下來的3該怎樣處理這樣三個關鍵性的問題。而在“三個”豎式完成之后，特意讓學生比對“三個”豎式，觀察商的小數點與被除數的小數點的位置關系，以及小數除法與整數除法哪些地方是相同的或不同的地方，旨在讓學生對除數是整數的小數除法的計算獲得一個清晰、完整的表象，讓這一計算方法得到了內化。】