內河船舶AIS與雷達動態信息集成性融合

范耀天， 王 馳

(1.武漢理工大學 航運學院，武漢 430063；2.內河航運技術湖北省重點實驗室，武漢 430063)

當前在船舶駕駛領域開展的信息融合研究主要集中在對多個船載傳感器進行數據融合，支持船舶智能避碰決策方面。由于目前船舶自動識別系統(Automatic Identification System, AIS)和雷達是船舶應用的主要導航設備，因此信息融合研究主要集中在AIS與雷達的數據關聯和數據融合上。這里主要研究AIS與雷達的數據融合問題。在運用統計加權法進行信息融合方面：CHANG[1]提出AIS與雷達根據誤差進行數據加權融合；鄭佳春等[2]將神經網絡引入到統計加權估計法中提高算法的精確性，使融合后數據的準確性得到一定的改善；林長川[3]根據時間和距離作相關決策，并在一個固定的范圍內獲取目標，利用柯西型隸屬函數進行精確的相關，提出一種改進的基于最大隸屬度的融合。在基于BP神經網絡算法進行信息融合方面，HU等[4]利用BP神經網絡理論關聯船用雷達和AIS的目標信息，對網絡結構的設計進行分析，基于MATLAB進行計算機仿真。在基于卡爾曼濾波算法進行信息融合方面，于海霞[5]對雷達數據和AIS數據進行多維性分析，運用穩態卡爾曼濾波方法實現時空校準、數據關聯和航跡融合，并通過試驗模擬評估這些算法的穩定性及精確度。

統計加權法可提高信息融合的精度和準確性，但會間接提高算法的復雜性，且融合算法需根據數據的類型來選擇；BP神經網絡信息融合的網絡結構參數及門限大小對結果的影響較大，且數據規模的大小對網絡參數的需求不同，需在研究過程中尋找規律；卡爾曼濾波算法對實際數據的可靠性及濾波器的穩定性有一定要求，當數據的可靠性不足或濾波器的穩定性不高時，對觀測值的平均值及卡爾曼濾波的估計值有很大影響。[6]集成多種融合方法可避免單一方法效果不理想的問題。

1 集成性模型

目前大多數研究主要采用單一的方法進行信息融合，主要原因是海上交通流密度不大，采用單一的方法即可滿足信息關聯的精度要求，而內河水域交通流密度大，交通流態勢復雜，需有更高的可靠性。

由于AIS數據的中心位置是CONNING的位置，而雷達回波是一種后向反射回波，回波的位置可能是艏部、舯部或艉部，因此有必要對雷達船位進行修正。首先對雷達采集的數據進行處理，假定船體形狀為橢圓形，則圖1中的全球定位系統(Global Positioning System，GPS)天線位置與船舶中心位置的坐標距離為

(1)

以本船雷達天線所在位置為中心建立直角坐標系，則圖2中的目標船中心位置的坐標為(M，N),船舶曲線表示為

E(x-M)2+2G(x-M)(y-N)+

H(y-N)2+f=0

(2)

若以橢圓中心點作為坐標軸原點，則橢圓的公式可表示為

(3)

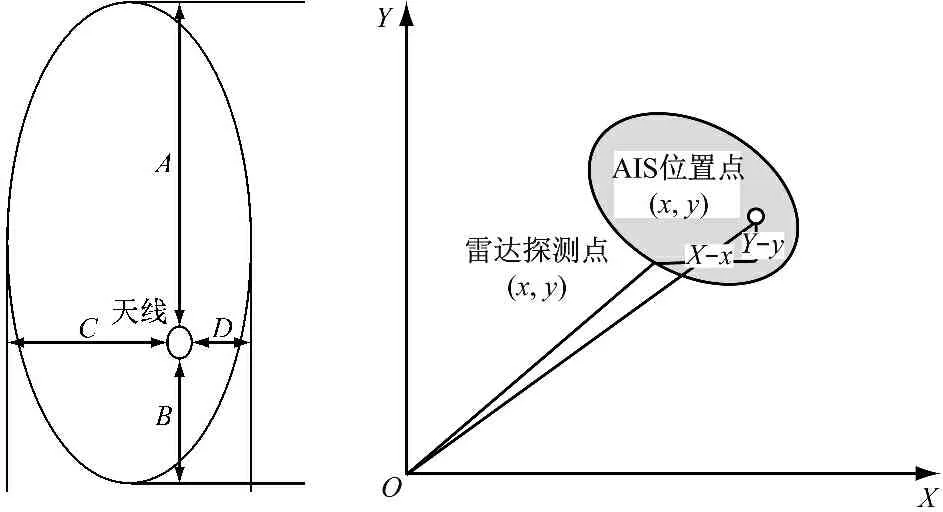
圖1 船載GPS天線位置 圖2 雷達船位修正示意

此外，將修正后的雷達數據與AIS數據進行融合計算，構建集成卡爾曼濾波、自適應加權和神經網絡等方法的多源異構數據融合模型(見圖3)。

2 數據融合

近年來已有多種信息融合模型被提出，多級處理是信息融合的主要方法，其中數據融合模型分為根據節點順序構建的功能型模型和根據數據提取構建的數據型模型2類。這里采用基于控制回路結構的混合型模型，基于信息融合處理中的循環特性，使處理任務的描述有較好的重現精度，并使融合行為發生位置容易從模型中得出；使用的方法主要包括自適應加權平均融合算法、BP神經網絡融合算法及卡爾曼濾波融合算法。

2.1 自適應加權航跡融合

2.1.1最優加權因子

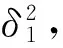
X=w1x1+w2x2

(4)

w1+w2=1

(5)

總體均方誤差為

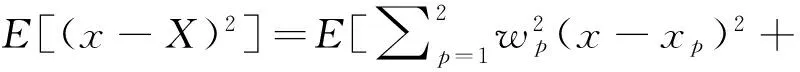
(6)

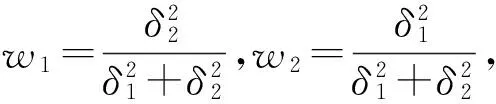
(7)

2.1.2加權融合算法

在已知AIS和雷達的測量方差及加權因子的情況下，可得到各自融合后的方差和融合之后的距離、方位、對地航速及航向，即

(8)

(9)

Xij(k)=wadXAi(k)+wrdXRi(k)=

(10)

Yij(k)=waθXAi(k)+wrθXRi(k)=

(11)

2.2 BP神經網絡融合

2.2.1融合模型的建立

分別設置網絡的輸入和輸出，隱含節點、網絡目標的誤差、訓練次數及學習率，并代入訓練數據進行訓練。[7]構建好融合模型后，首先對網絡進行訓練，使網絡達到設置要求，然后輸入關聯的AIS和雷達數據，得到網絡輸出的合并信息。[8]

2.2.2網絡的測試和驗證

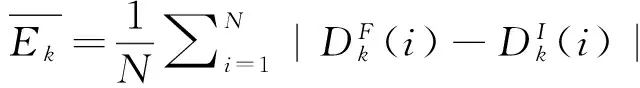
2.3 卡爾曼濾波融合

對雷達和AIS進行融合的基本原理是在空間上和時間上依據某種準則對2臺傳感器的信息進行結合，得到一個更合理、精度更高的融合數據，使之擁有比單傳感器更高的精準度。卡爾曼狀態估計的功能可實現對雷達和AIS的數據進行平滑，對所測的船舶數據進行濾波和對船舶未來的航行軌跡進行預測。卡爾曼濾波理論是依據狀態方程工具應用時域法遞推得出最優估計值。[10]

這里進行數據融合，對目標的狀態估計可表示為

I-K(k+1)H(k+1)=

P(k+1|k+1)P(k+1+k)-1

(12)

對雷達和AIS，都有

Hi(k+1)=Pi(k+1|k+1)Pi(k+1+k)-1

(13)

(14)

由此可得

(15)

(16)

Pi(k+1|k+1)-1=Pi(k+1|k)-1+

(17)

P(k+1|k)=Φ(k)P(k|k)Φ(k)′+

G(k)Q(k)G(k)′

(18)

3 集成性融合

3.1 數據集成性融合

利用不同方法得出的融合數據與真實數據可能相差較大，分別比較3種融合方法的融合數據與真實數據的誤差大小，運用加權平均法得出3種融合方法的加權權重，得出最終的融合數據。由加權平均公式可得3種融合方法的權重大小。

(19)

(20)

(21)

(22)

(23)

(24)

根據加權平均公式可得自適應加權航跡融合法的x坐標權重和y坐標權重分別為ωx1=σ2+σ3/2[(σ1+σ2+σ3)]及ωy1=(δ2+δ3)/(δ1+δ2+δ3)；BP神經網絡融合的x坐標權重和y坐標權重分別為ωx2=σ1+σ3/[2(σ1+σ2+σ3)]及ωy2=(δ1+δ3)/[2(δ1+δ2+δ3)]；卡爾曼濾波融合的x坐標權重和y坐標權重分別為ωx3=σ1+σ2/[2(σ1+σ2+σ3)]及ωy3=(δ1+δ2)/[2(δ1+δ2+δ3)]。

航跡融合可表示為

(25)

(26)

式(25)和式(26)中：xaw(k)為k時刻自適應加權航跡融合航跡點x坐標；xBP(k)為k時刻BP神經網絡融合航跡點x坐標；xkm(k)為k時刻卡爾曼濾波融合航跡點x坐標；yaw(k)為k時刻自適應加權航跡融合航跡點y坐標；yBP(k)為k時刻BP神經網絡融合航跡點y坐標；ykm為k時刻卡爾曼濾波融合航跡點y坐標。

3.2 集成系統精確性和穩定性

3.2.1精確性

分別定義k時刻的自適應加權融合航跡點坐標為(xaw(k)，yaw(k))，BP神經網絡融合航跡點坐標為(xBP(k)，yBP(k))，卡爾曼濾波融合航跡點坐標為(xkm(k)，ykm(k))，集成融合航跡點的坐標為(xt(k)，yt(k))，真實航跡點的坐標為(x(k)，y(k))；誤差的波動性低,則融合精度高。誤差的波動性計算式為

(27)

(28)

自適應加權融合的精確性可表示為

(29)

BP神經網絡融合的精確性可表示為

(30)

卡爾曼濾波融合的精確性可表示為

(31)

集成性融合的精確性可表示為

(32)

3.2.2穩定性

航跡融合的穩定性即相鄰航跡點之間的差值大小Δk的總和。

(33)

(34)

自適應加權融合的穩定性可表示為

(35)

BP神經網絡融合的穩定性可表示為

(36)

卡爾曼濾波融合的穩定性可表示為

(37)

集成性融合的穩定性可表示為

(38)

4 模擬及驗證

為充分體現內河船舶的航行特點，不僅應收集實船直線航行時的雷達和AIS數據，還應采集船舶大幅度機動時的數據。由于內河水域船舶操縱空間具有一定的局限性及在內河水域復雜環境下進行船舶試驗可能引發事故，因此模擬驗證的數據收集選擇在白天能見度良好的沿海開闊海域進行。由于大型船舶在轉向和變速方面較為遲鈍，同時為保證試驗的安全性和維護正常的航行秩序，試驗船舶采用操縱靈活的引航艇，試驗航線為從山東青島大港六號碼頭至膠州灣團島附近航段。試驗過程具體為：2015年11月5日以青島港引航站的“引航2號”船作為目標船，在青島舶舶交通管理中心(Vessel Traffic Services,VTS)以VTS雷達模擬本船雷達，實時跟蹤“引航2號”船的運動，并收集目標船及附近船舶的經緯度、航速和航向等AIS及雷達數據；同時，在目標船上安裝差分全球定位系統(Differential GPS,DGPS)，其天線架設在目標船自有的GPS天線附近，對其經緯度、航速及航向數據進行測量和采集。由于DGPS的精度較高，在后續的驗證階段，信息融合模型以目標船舶的DGPS數據作為基準數據進行比對。

通過數據關聯得到與AIS相關聯的雷達數據，根據第“3”節中提出的3種融合方法及公式對試驗采集到的AIS數據和雷達數據進行計算，得到航跡加權法x坐標和y坐標的誤差平方和分別為σ1=1 972.342及δ1=8 245.462，BP神經網絡x坐標和y坐標的誤差平方和分別為σ2=4 624.231及δ2=26 235.791，卡爾曼濾波的x坐標和y坐標的誤差平方和分別為σ3=4 245.348及δ3=26 682.496。

根據加權平均公式可得：

1) 自適應加權航跡融合法的x坐標和y坐標權重分別為ωx1=0.409 0及ωy1=0.432 5。

2) BP神經網絡融合的x坐標和y坐標權重分別為ωx2=0.286 7及ωy2=0.285 5。

3) 卡爾曼濾波融合的x坐標和y坐標權重分別為ωx3=0.304 2及ωy3=0.281 9。

由此,航跡融合可表示為

xr=0.409 0xaw(k)+0.286 7xBP(k)+

0.304 2xkm(k)

(39)

yr=0.432 5yaw(k)+0.285 5yBP(k)+

0.281 9ykm(k)

(40)

相關數據融合航跡見圖4。

1) 精確性：計算得到Baw=114.937 4，BBP=696.782 1，Bkm=252.627 4，Bj=80.323 2。由此可看出,集成融合的精確性得到了較大改善。

5 結束語

本文分析了內河船載雷達和AIS在船舶動態感知及辨析中的局限性及互補性，構建了集成AIS和雷達的多源異構數據融合模型，通過算例驗證了該模型可在保證模型可靠性的基礎上大大提高模型的精確性和穩定性。

[1] CHANG S J. Development and Analysis of Applications as an Efficient Tool for Vessel Traffic Service[C]//Oceans,2004,4(4):2249-2253.

[2] 鄭佳春,陳宗恒.基于模糊神經網絡的AIS與雷達目標數據融合[J].集美大學學報,2005,10(3):216-220.

[4] HU X, LIN C. A Preliminary Study on Targets Association Algorithm of Radar and AIS Using BP Neural Network[C]//Procedia Engineering, 2011:1441-1445.

[5] 于海霞.AIS與雷達數據融合方法的研究[D].大連:大連海事大學,2006.

[6] 劉慶華，仲海嘯，陶峰，等. 卡爾曼濾波融合新算法及其船舶高精度液位測量的應用[J].中國造船, 2016, 57(2):192-200.

[7] 郭文剛. 基于BP神經網絡的船舶航跡控制技術[J]. 艦船科學技術, 2014(8):87-93.

[8] 胡曉瑞. 基于BP神經網絡的雷達與AIS目標信息融合處理研究[D]. 廈門：集美大學，2012.

[9] 張莉. BP神經網絡在船舶運動估計中的應用[J]. 艦船科學技術, 2016(12):13-15.

[10] 徐鐵，蔡奉君，胡勤友，等. 基于卡爾曼濾波算法船舶AIS軌跡估計研究[J]. 現代電子技術, 2014(5):97-100.