海底管線平管起吊的參數靈敏度

趙望奇， 朱克強， 葉世杰, 張永明， 周 晨， 金躍波

(1. 寧波大學 海運學院， 浙江 寧波 315211; 2. 寧波東方電纜股份有限公司， 浙江 寧波 315801)

隨著海洋石油開采技術的不斷發展，海底管道的作用愈加顯著，不僅可在水下井口與平臺或浮式生產儲油卸油裝置(Floating Production Storage and Offloading, FPSO)之間進行注水作業，還可在平臺之間、平臺與岸上儲油設施之間進行原油運輸作業。但是，受鋪設距離較長、運行環境復雜多變等因素影響，海底管道在鋪設和起吊過程中會發生很大的彎曲變形。因此，對海底管道的下放和提升2個施工階段進行力學分析很有必要，以保證其安全性。

在實際完成淺海牽引式鋪管、立管與海底平管的連接等海工作業時，需將海底管道從海底起吊至海面進行施工。[1-4]在起吊過程中，海底管道從離泥點處到起吊端部為懸跨段(見圖1)，會在實際作業中發生大撓度變形，管道的彎曲應力會急劇增大，從而引起管道的局部破損。針對該問題，國內外已有相關學者[5-10]進行相應的分析研究。黃玉盈等[11]以彈性桿理論為基礎，考慮地基變形和摩擦力對管線的影響，提出海底管線在鋪設時的二維靜力模型，并率先采用冪級數法與奇異攝動法相結合的方法對力學模型進行求解。曾霞光等[12]將二階微分方程和三階微分方程與不同邊界條件組合，提出管線單點起吊的3種不同分析模型，并對這3種模型進行不同工況下的數值分析，得出各自的起吊適應范圍。焦冬梅等[13]利用有限元軟件SUSPEND和OFFPIPE對雙層管及等效單層管的起吊進行分析研究，然而SUSPEND只能進行等效單層管起吊模擬，且其在分析過程中并未考慮浮筒及豎直向下的土壤抗力對管線起吊的影響。因此，本文利用OrcaFlex中的Link來模擬土壤抗力[14]，并充分考慮波流的作用、船舶與管線的耦合運動，更加真實地模擬平管起吊過程，為平管起吊提供一定的數據和理論基礎。

1 平管起吊力學模型

由于海底管線在起吊過程中既要受到來自于吊車的豎直提升力，又要承受風、浪、流的聯合作用，因此選取幾何非線性梁模型作為平管起吊的力學模型。此外，考慮到海底管線在海床上鋪設的距離較長，將離泥點位置作為梁模型的固定端，根據大撓度梁變形理論對管線起吊過程中的懸跨段建立平衡微分方程，受力模型見圖2。平管起吊分為J型起吊和S型起吊2種形式。一般情況下，J型起吊應用于立管與海底平管的焊接中，管線出水之后與施工船甲板呈10°以上的夾角，利于與立管對接；而S型起吊廣泛應用于海底管線維修和回收中，要求管線出水之后必須使自由端接近水平，以利于2段管道對接及降低焊接導致的初始應力。本文以拋錨導致的海底管線損傷為例進行平管起吊數值模擬，因此采用S型起吊力學模型。

1.1 平衡微分方程

根據圖2的力學模型，海底管線的平衡微分方程可表示為

(1)

式(1)中：q為管道在海水中單位長度的質量；ds為所選微分段的弧長；Ft為沿管軸線均勻分布的切向波流力；Fn為垂直于管軸線均勻分布的徑向波流

力；N為管線軸向拉力；Q為管線端部剪切力；θ為管道軸線與水平面的夾角；M為管線端部彎矩。Ft和Fn可采用莫里森公式來計算。

(2)

(3)

(4)

(5)

式(2)～式(5)中：Fnc和Ftc分別為海流力的徑向分力及切向分力；Fnw和Ftw分別為波浪力的徑向分力及切向分力；Cn和Ct分別為徑向拖曳力系數及切向拖曳力系數，考慮到管線起吊施工海域一般為<30 m的淺海海域，將二者設置為相同的數值，且隨雷諾數發生相應變化；Cm為慣性力系數，取值為2；vn=vsinθ和vt=vcosθ分別為海流的徑向速度及切向速度；un=usinθ和ut=ucosθ分別為海浪的徑向速度及切向速度。

1.2 數值求解

由于海底管線起吊屬于大長徑比、大彎曲變形問題，故可忽略管線的軸向變形和剪切變形，僅考慮管線的彎曲變形。由此可得

(6)

(7)

式(6)和式(7)中：EI為海底管線剛度；b為懸掛段長度；y(s)和u(s)分別為管線上任一點的撓度及水平位移；其余參數與上述相同。此外，S型起吊的邊界條件可簡化為

1) 在離泥點處，即s=0處，y(0)=0，(0)=0，u(0)=0，N(0)=0，M(0)=0；

2) 在管線自由端處，即s=b處，N(b)·sinb-Q(b)·cosb=F，M(b)=M。

將無量綱參數s/b引入到式(1)中，使求解區間由(0,b)變為(0,1)，撓度、彎矩和剪力等其他參數也進行無量綱簡化，即

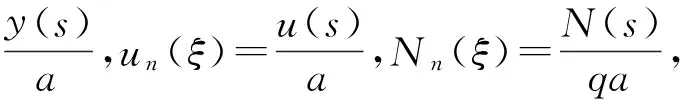
(8)

將式(6)～式(8)代入到式(1)中可得

(9)

2 平管起吊有限元模型

2.1 平管起吊基本參數

選取“渤中35-2”號油田井口平臺與“墾利10-1”號油田中心平臺之間的海底管線為建模對象。

該管線是一條總長度為32 km的輸氣管線，所跨海域的水深變化范圍為15.8～19.8 m，管道線路的平均坡度為0.1‰，設計使用壽命為30 a。考慮到管線所在海域的水深較淺，且在其服役期間因船舶拋錨而導致破損的可能性較大，選取該管線的一部分進行拋錨致管線破損的平管起吊模擬。

該部分管線具體參數見表1。利用OrcaFlex軟件建立海底管線3點起吊模型(見圖3)，其中，海底管線采用Line單元模擬，因為Line單元具有彈簧阻尼振子的特性，可承受拉、壓及彎的作用，且支持解決非線性大撓度變形問題，非常適合進行管道起吊過程中的非線性動力分析。模型中海底管線的長度為1 555 m，提管端采用自由約束，另一端因管線較長而采用錨固約束。為能精確模擬管線起吊過程中懸跨段的受力情況，對距離提管端300 m以內的管線進行精細的網格劃分，網格大小為1 m，該段之外的管線網格大小為5 m。

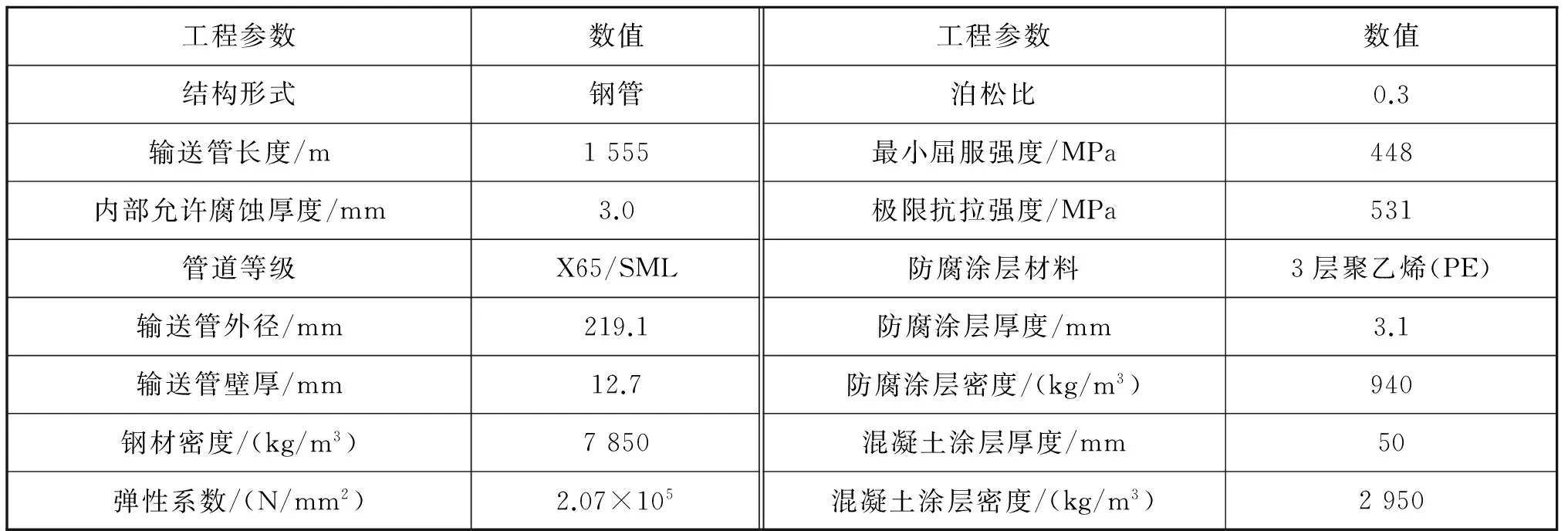
表1 管線具體參數

模型中采用3臺絞車起吊管線，根據離管端水平距離的不同，由近到遠標記為1號舷吊、2號舷吊和3號舷吊。由于吊索的長度在整個動態起吊過程中一直發生變化，因此采用可改變長度的Winch單元來模擬吊索，Winch單元的一端與海底管線相連接，另一端與海面施工船相連接。在吊索動態分析過程中，主要通過控制吊索長度來控制整個起吊過程，各階段吊繩伸長和縮短的長度需根據船上的卷揚機及其他設備等參數來確定。在模擬中，為使模型更容易收斂，吊繩的收縮過程通過24個分析步實現。由于海底管線一般會埋于海床之下，因此在管線起吊過程中必然會發生非線性的管土相互作用，該作用力可簡化為豎直方向的土吸力。

由于OrcaFlex無法直接對管道施加土壤吸力，因此為模擬土吸力對海底管線的作用，采用Link單元模擬豎直方向的土壤抗力。此外，考慮到距管線自由端200 m外管線段的土壤抗力對提管作業的影響較小，僅在提管段200 m以內采用間距為1 m的201個Link單元模擬土吸力。通過Link單元模擬，可使該數值模型更加符合現實中的平管起吊，其數據也更加可信。對于Link單元的剛度設置,可通過公式得到,即

F=Rsoil+Nsoil

(10)

Nsoil=ksoilD(H+D)

(11)

式(10)和式(11)中：F為模型中的拉力參數；Rsoil為土壤阻力；Nsoil用于抵消土壤抗力；ksoil為土壤剛度；H為埋深；D為管道直徑。

為降低吊繩起吊的負擔，在海底管線合適位置處安裝浮袋，采用3D浮標單元模擬浮袋，浮袋的體積為5 m3，質量為0.005 t，高度為2.1 m。施工船的船長為98.5 m，型寬為29 m，型深為7.68 m，滿載吃水為4.4 m。平管起吊模型見圖3。

2.2 環境參數

假定海底管線破損段靠近BZ45-2平臺所在海域，該海域的平均水深為17 m，最高天文潮高為1.9 m，因此模擬的計算水深為18.9 m。BZ45-2平臺附近海域的極端環境參數見表2。由表2可知，1 a重現期的海況對于海底管線起吊而言過于危險，因此選取潛水員作業時的海況進行分析。該海況下的波浪為隨機波，可采用JONSWAP波浪模型，最大波高為1 m，波向為000°，譜峰周期為11.35 s，海流速度為0.2 m/s，海流的流向為090°。海床的形狀、坡度及剛度對海底管線起吊的影響也不可忽略，但為方便建模，將海床簡化為平面海床，其垂向剛度系數為1.866 kN/m3，剪切剛度系數為100 kN/m3。

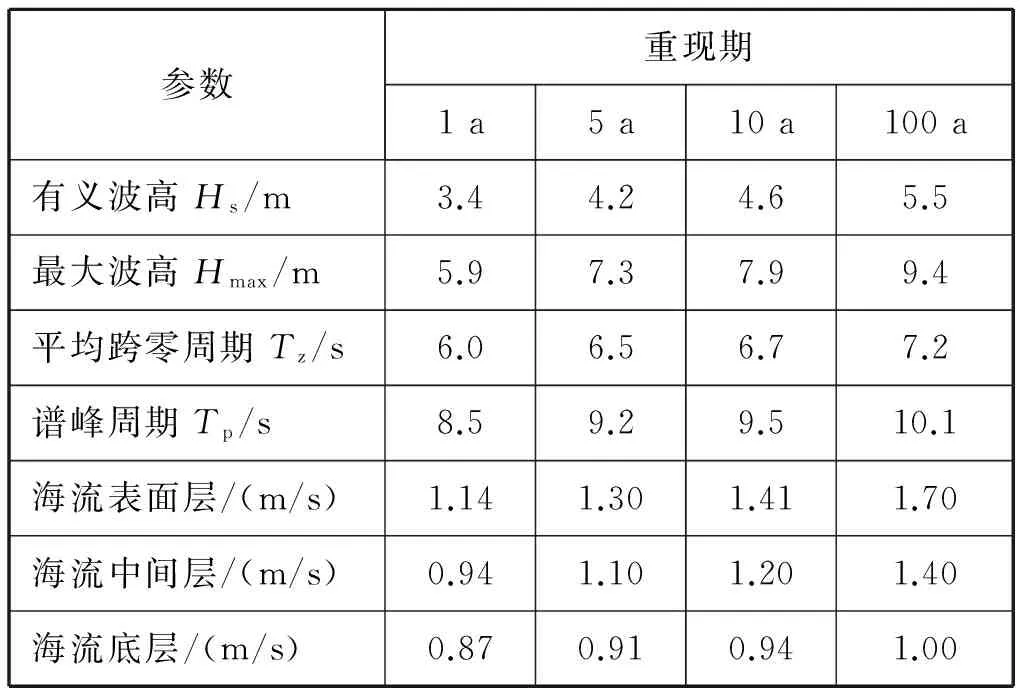
表2 BZ45-2平臺附近海域環境參數

3 參數敏感性分析

在海底管線起吊過程中，舷吊的分布位置和起吊速度、浮袋的大小和數量、海浪的大小和方向及海床剛度等因素均會影響海底管線的強度。基于此，針對1號舷吊的布置位置、浮筒的布置位置和浮筒間距對管線強度的影響進行參數敏感性分析。

為更加有效地分析各參數的敏感性，將1號舷吊布置在距離管端水平距離5 m處，起吊時間為198 s，浮筒數為1個，且浮筒距離管端水平距離為73 m。布置完成之后分析整根管線的有效張力和舷吊。圖4為船上3個舷吊的張力時程。由圖4可知，1號舷吊、2號舷吊和3號舷吊的最大張力分別為127 kN,107 kN,175.372 kN。在起吊開始之后的20～150 s時間段內的張力變化幅度均很小，但在前20 s及150 s以后，各舷吊的張力均會大幅度變化。這是由于在前20 s內，舷吊需將管道從海底拉起，要克服由Link模擬的土壤阻力；在150 s以后，前段管道開始被拉出水面，管道所受浮力減小，舷吊需施加的張力隨之增大。3號舷吊由于需承擔水中管道的部分質量，其張力值要大于1號舷吊和2號舷吊。

圖5為管線最大有效張力和最大曲率沿管長的分布。由于本文只研究平管起吊過程的參數敏感性，因此只需對前200 m的管道進行分析。由圖5可知:管道的最大有效張力在距管端水平距離70 m處，大小為233 kN；最大曲率在距管端水平距離65 m處，大小為0.042 3。由于舷吊點布置在管道的前100 m處，因此管道的最大曲率在前100 m處會出現較大起伏，導致在該段易產生應力集中現象。

3.1 1號舷吊位置的參數靈敏度分析

為研究1號舷吊位置的參數靈敏度，將1號舷吊分別布置在距左邊管端水平距離3 m,4 m,5 m,6 m和7 m處，記為工況1～工況5。2號舷吊和3號舷吊的布置位置為距左邊管端水平距離35 m和75 m處，起吊時間為194 s，浮筒距左邊管端的水平距離為73 m。

圖6為不同工況下3個舷吊的最大張力。圖7為不同工況下管道最大有效張力和最大曲率。從圖6中可看出：3號舷吊的最大張力要大于1號舷吊和2號舷吊；1號舷吊的最大張力要稍大于2號舷吊。同時，3號舷吊的最大張力幾乎不隨1號舷吊位置的改變而改變，2號舷吊的最大張力則因1號舷吊和2號舷吊距離的逐漸減小而出現小幅增大，即2號舷吊和3號舷吊的最大張力對1號舷吊的位置參數并不靈敏。1號舷吊的最大張力對其自身的位置參數還是相對靈敏的。由于在工況3下1號舷吊的最大有效張力最小，且由圖7可知在工況3下海底管線在起吊過程中所受的最大有效張力和最大曲率也最小，因此當1號舷吊處于距管線左端5 m處時，更能保證管線在起吊過程中的強度及穩定性。

3.2 浮筒位置的參數靈敏度分析

為了解浮筒位置的參數靈敏度，將浮筒分別布置在距左邊管端水平距離73 m，78 m，83 m，88 m，93 m處，記為工況1～工況5。1號舷吊、2號舷吊和3號舷吊分布在距左邊管端水平距離8 m，35 m和75 m處，起吊時間為194 s。

圖8為在不同工況下3個舷吊的最大張力。圖9為在不同工況下管道的最大有效張力和最大曲率。從圖8中可看出：1號舷吊和3號舷吊對浮筒的位置有較高的靈敏度，其最大張力隨浮筒距管道左邊端點水平距離的增加而減小；2號舷吊的最大張力出現小幅的增加。觀察圖9可發現，管道的最大有效張力和最大曲率對浮筒位置有較大的靈敏度，即全部出現較大幅度的減小。1號舷吊和3號舷吊最大張力及管道最大有效張力和最大曲率出現這種現象的原因是，在管道起吊即將完成階段，浮筒會升至水面。當浮筒距管道左端的距離增大時，浮筒升至水面以上的體積會變小，從而導致浮力增大，1號舷吊和3號舷吊最大張力及管道最大有效張力和最大曲率也會隨之減小。當浮筒不再浮出水面時，1號舷吊最大張力的減小幅度會有一定程度的降低，管道的最大曲率甚至出現增大。但是，3號舷吊的最大張力和管道最大有效張力仍出現較大幅度的減小。

3.3 浮筒間距的參數靈敏度分析

當浮筒的數量增加時，舷吊最大張力和管道最大有效張力及最大曲率都會減小，但浮筒間距的參數靈敏度無法得知。由此，對浮筒之間的間距進行研究。將浮筒的數量設置為3個，3個浮筒等間距布置，1號浮筒布置在距左邊管端73 m處，浮筒之間的間距分別為10 m，20 m，30 m，40 m，50 m，記為工況1～工況5。

圖10為在不同工況下3個舷吊的最大張力。圖11為管道在不同工況下的最大有效張力和最大曲率。從圖12中可看出：在工況1中，1號舷吊的最大張力為所有工況中最大的，達到105.9 kN；而在其余工況下，最大張力變化較小，一直維持在81 kN左右。2號舷吊的最大張力在工況1中最小，大小為78.705 kN；其余工況下的最大張力也一直維持107 kN左右。因此，1號舷吊和2號舷吊在間距較小時對浮筒間距有較高的靈敏度。對于3號舷吊，最大張力隨浮筒間距變大而先減小后增大，最小值在工況3中出現，且靈敏度高于2號舷吊和3號舷吊。管道的最大有效張力和最大曲率會隨浮筒間距的增大而先增大后減小，但最大有效張力的最小值出現在工況4，而最大曲率的最小值出現在工況3。因此，工況3為在所有工況中最理想的工況。出現這些現象的原因是，在前3個工況中，由于浮筒距離舷吊較近，浮筒能提供的浮力大于管線的重力。但是，隨著浮筒與舷吊之間的距離增大，浮筒重力提供的浮力漸漸小于管道的重力。

4 結束語

1) 3個舷吊的最大張力對1號舷吊的布置位置靈敏度較低，而1號舷吊的布置位置對管道的最大有效張力和最大曲率而言屬于高靈敏度參數。在實際工程中，為防止出現應力集中現象，應使1號舷吊和2號舷吊之間的水平間距和2號舷吊與3號舷吊之間的水平間距相同，避免1號舷吊的距管端的水平距離過大或過小。

2) 浮筒布置位置對于1號舷吊和3號舷吊及管道的最大有效張力和最大曲率全部屬于高靈敏度參數，其最大張力會隨著浮筒距管道左端的水平距離的增加而減小。因此，在實際工程中可通過適當加大浮筒距管道左端水平距離來減小舷吊和管道的張力及管道的曲率。但是，該距離過大反而會導致管道曲率增大。

3) 浮筒間距對于3號舷吊及管道最大有效張力和最大曲率屬于高靈敏度參數，1號舷吊和2號舷吊對浮筒間距只在該長度較小時有較高的靈敏度。在實際工程中，當浮筒個數較多時，浮筒之間的間距不應過大或過小，應根據起吊管線的長度和浮

筒提供的浮力選取合適的值。

[1] GUARRACINO L, MALLARDO V.A Refined Analytical Analysis of Submerged Pipelines in Seabed Laying [J]. Applied Ocean Research, 1999, 21(6): 281-193.

[2] SHAMPIRE L F, GLADWELL I, THOMPSON S. Solving ODEs with MATLAB [M]. New York: Cambridge Univerity Press, 2003:133-211.

[3] WITZ J A. TAN Z. Rotary Bending of Marine Cables and Umbilicals [J]. Engineering Structures, 1995, 17(4): 267-275.

[4] 張大朋, 朱克強, 荊彪, 等. 文昌臍帶纜J型牽拉入位操作的水動力分析 [J]. 船舶工程, 2015, 37(4): 92-97.

[5] BERNITSAS M M,VLAHOPOULOS N. Three-Dimensional Nonlinear Statics of Pipelaying Using Condensation in an Incremental Finite Element Algorithm [J]. Computers & Structures, 1990, 35(3): 195-214.

[6] SCHMIDT W. Submarine Pipeline Analysis with anElastic Foundation by the Finite Element Method [J]. Journal of Manufacturing Science and Engineering, 1977, 99(2): 480-484.

[7] MALAHY J R C. A Nonlinear Finite Element Method for the Analysis of the Offshore Pipelaying Problem (Beam Element, Geomtric) [D]. Texas: Rice University, 1985.

[8] CIACCIA M, MARTINEZ C, GONCALVES R. Nonlinear 3D Finite Element Formulation for the Analysis of Submarine Pipelines During Laying Operations [C]∥ASME 2002 International Mechaical Engineering Congress and Exposition, 2002: 55-63.

[9] HALL J E, HEALEY A J. Dynamics of Suspended Marine Pipelines [J]. Journal of Energy Resources Technology, 1980, 102(2): 112-119.

[10] CLAUSS G, WEEDE H, RIEKERT T. Offshore Pipe Laying Operations—Interaction of Vessel Motions and Pipeline Dynamic Stresses [J]. Applied Ocean Research, 1992, 14(3): 175-190.

[11] 黃玉盈, 王忠民, 楊挺青. 海洋管線在有摩擦的彈性地基上鋪設時的大變形分析 [J]. 應用力學學報, 1988, 5(4): 110-118.

[12] 曾霞光, 段夢蘭, 陳景皓. 海洋管道單點提放的若干數學模型研究 [J]. 海洋工程, 2013, 31(1): 32-37.

[13] 焦冬梅, 燕暉, 王振興. 海底管道立管起吊分析方法綜述[J]. 石油化工建設,2013(3): 41- 42.

[14] ORCINA. OrcaFlex User Manual[M]. Version 10. Cumbria, Orcina, 2015.