讓“學”與“教”自然對稱
——《圖形的運動——軸對稱》教學設計(一)
嚴紅興
【教學過程】
一、反饋導學單,整體感知軸對稱圖形
圖1

圖2
首先讓我們來看看同學們導學單完成的情況。
1.圖1是軸對稱圖形嗎?它的對稱軸在哪里?誰來指一指?
2.圖2的對稱軸在哪里?你能指出來嗎?還有不同的嗎?
預設:我們發現同一個軸對稱圖形可以有多條不同的對稱軸。
3.你覺得圖3這個軸對稱圖形的另一半可以畫在哪里?
預設:沿著四條不同的對稱軸進行對稱。

圖3
呈現:你有辦法驗證圖4、5、6的軸對稱圖形嗎?

圖4
圖5

圖6
圖7
預設:請你想象沿著對稱軸對折一次。(課件操作動畫鏈接驗證)
4.圖7的對稱軸在哪里?指明畫出的另一半在哪里?
驗證:沿著這條對稱軸對稱過去,它們能重合嗎?(操作動畫鏈接驗證)
歸納:觀察四組對稱圖形有什么相同?有什么不同?
預設:選擇不同的對稱軸,畫出來的圖形位置就不一樣。
板書:形狀大小不變、位置變化。
過渡:從導學單中,老師還了解到同學們還有一些問題:

【設計意圖:前測中,我們發現大部分學生已經能夠找到簡單圖形的對稱軸,對于有多條對稱軸的圖形找對稱軸,還存在一定的遺漏情況。通過這一組題的反饋,激發學生原有經驗,豐富了學生對于軸對稱圖形的表象。】
二、下對稱棋,逐步探究對稱點的特征
1.下對稱棋,探索對稱點到對稱軸的距離相等。
過渡:下面就讓我們借助“對稱棋”游戲來研究“對稱點的連線和對稱軸之間的聯系”。
教師示范一組A、A',繼續在對稱軸左邊下好一顆B,接下來該怎么下呢?
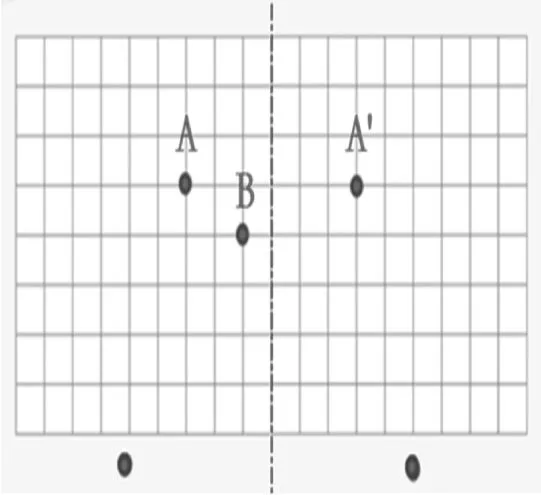
預設:學生在對稱軸右邊指出B點的對應點,并闡述自己的想法。
點撥:如果現在老師繼續下一顆C,你能下出關于它的對稱棋嗎?

2.連接對稱點成軸對稱圖。
連點成形:現在,老師把左右兩邊的對稱點都連起來。猜猜是一個什么圖形?
觀察歸納:仔細觀察這兩個對稱的三角形,有什么發現?
預設:兩個三角形對應的頂點到對稱軸的距離相等。
驗證:你能從三角形中任意找一點來驗證這個結論嗎?
預設:從三角形中任意找出一對對稱點連接驗證。
小結:剛才同學們通過下對稱棋又發現了一個特征,即軸對稱圖形中的所有對稱點到對稱軸的距離相等,并且它們之間的連線與對稱軸垂直。
【設計意圖:通過下對稱棋寓教于樂,自主發現對稱點與對稱軸的關系,連點成面后形成三角形,在寓教于樂的游戲過程中發現軸對稱圖形的特征。】
三、利用對稱點的關系畫出三角形的軸對稱圖形,理解軸對稱圖形的本質
1.畫三角形的軸對稱圖形。
直觀想象:現在再給你一個三角形,你能畫出它的軸對稱圖形嗎?
預設:想象、辨析、判斷、說理。
點撥:準確的三角形到底在哪里?具體是怎么樣的?請你運用剛才發現的軸對稱圖形的特點,自己動筆在紙上畫一畫。
預設:在方格紙上獨立嘗試畫出軸對稱后的三角形。
介入:(教師巡視觀察)如果有困難,可以打開平板里畫三角形的視頻來自學;如果畫好了,也可以對照平板視頻驗證自己畫的三角形是否正確。

反饋錯例,總結畫法:
(1)呈現:(對稱點距離數錯畫成平移變換的和沒有標對應點的)請仔細觀察以上幾幅作品,你有什么想說的?
(2)我們應該怎樣畫出一個正確的軸對稱圖形?
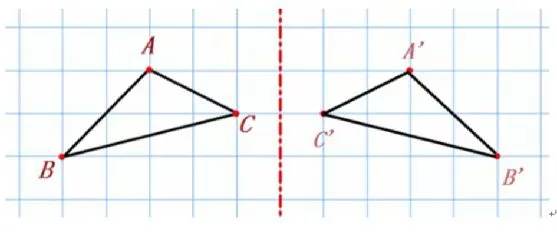
預設:先畫圖形的對應點,然后連接各個對應點。
2.變換位置畫圖形,深入理解軸對稱圖形的特征。
變式:
(1)如果把原來的三角形往左移動,它的軸對稱圖形會怎么變化?(邊說邊用白板移動)
(2)把原來的三角形往右移動呢?C點的對稱點又在哪里?
(3)如果三角形不動,把對稱軸進行平移或旋轉,你還能畫出三角形的軸對稱圖形嗎?
預設:借助三角板獨立畫圖。
教師巡視,收集典型的錯誤作品并反饋,進行歸納總結。
討論:為什么對稱點到對稱軸的連線要畫上直角符號?這條線是用來做什么的?
預設:因為它們的連線和對稱軸垂直,借助對稱點到對稱軸的距離相等可以畫出對應點。
【設計意圖:通過畫出三角形的軸對稱圖形,鞏固軸對稱圖形的特征;在多次變換的過程中進一步理解軸對稱圖形的內在關系;尤其是在對稱軸旋轉后,由水平方向對稱變成了非水平方向對稱,提升了空間想象的要求,促使學生運用軸對稱變換的本質屬性解決問題。】
四、設計應用,體會價值
1.判斷下列圖形是否為軸對稱圖形,如是請畫出對稱軸。

預設:針對誤選的平行四邊形,運用軸對稱圖形的特征討論糾錯,結合判斷過程課件動態演示。
2.運用軸對稱變換設計圖案。
預設:根據所選圖形,運用軸對稱變換,獨立設計出密鋪及類似圖形并小組交流。
反饋欣賞:展示基本圖形變換出美麗圖案的過程,拓展到實際生活中的軸對稱應用。
【設計意圖:通過對簡單平面圖形的判斷,讓學生認識到一般平行四邊形是非軸對稱圖形。用簡單的平面圖形借助軸對稱變換設計出新的圖案,感受軸對稱變換的應用價值。】
五、課堂小結,回顧感悟
回顧整理:對照課前的疑問,你的問題都解決了嗎?

【設計意圖:在回顧與反思中整理全課內容,回應課前學生提出的疑惑。】

