數學文化高考題舉隅(II)*

北京豐臺二中(100071) 甘志國

數學文化高考題舉隅(II)*

北京豐臺二中(100071) 甘志國

1.5 勾股定理

題目22(1979年高考全國卷文科、理科第4題)敘述并證明勾股定理.

解勾股定理：直角三角形兩直角邊的平方和等于斜邊的平方.

下面給出三種證法：

證法1 (中國古代數學家趙爽給出的證明)簡述如下：

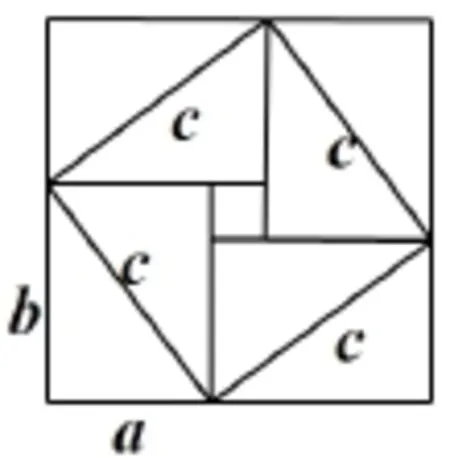
圖18

證法2 (美國第二十任總統JamesAbramGarfield(1831～1881)于 1881年給出的證明)簡述如下：

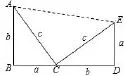
圖19

證法3 如圖20所示,圓O是Rt△ABC的內切圓,有.

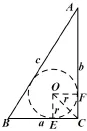
圖20

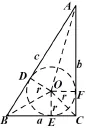
圖21

注由證法3的思路,還可給出余弦定理的證明(2011年高考陜西卷文科、理科第18題就是“敘述并證明余弦定理”)：

在△ABC中,分C為銳角、直角、鈍角及S△ABC=.

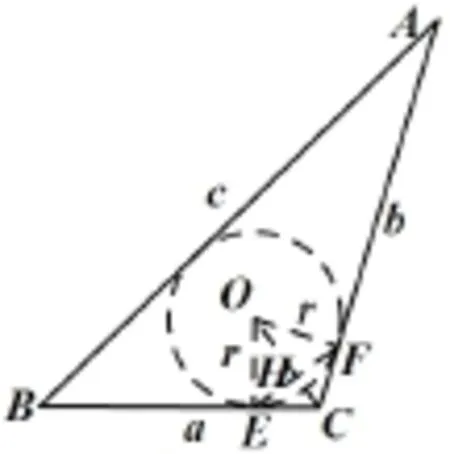
圖22

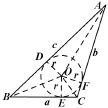
圖23

1.6 蝴蝶定理

題目23 (2003年高考北京卷理科第 18題)如圖24,橢圓的長軸A1A2與x軸平行,短軸B1B2在y軸上,中心為M(0,r)(b＞r＞0).

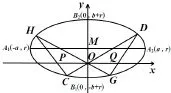
圖24

(1)寫出橢圓的方程,求橢圓的焦點坐標及離心率;

(2)直線y=k1x交橢圓于兩點C(x1,y1),D(x2,y2) (y2＞0).直線y=k2x交橢圓于兩點G(x3,y3),H(x4,y4) (y4＞0).求證：;

(3)對于(2)中的C,D,G,H,設CH交x軸于點P,GD交x軸于點Q.求證：|OP|=|OQ|.

(證明過程不考慮CH或GD垂直于x軸的情形.)

解(1)橢圓方程為,左、右焦點的坐標分別為F1(-√a2-b2,r),F2(√a2-b2,r),離心率

評析本題的背景是蝴蝶定理.蝴蝶定理最先是作為一個征求證明的問題,刊載于1815年的一份通俗雜志《男士日記》(Gentleman’sDiary)第39-40頁上;而“蝴蝶定理”這個名稱最早出現在《美國數學月刊》1944年2月號,由于其幾何圖形形象奇特,貌似蝴蝶,便以此命名.

蝴蝶定理的內容是：如圖25所示,圓O的弦PQ的中點為M,過點M任作兩弦AB,CD,弦AD與BC分別交弦PQ于點X, Y,則M為線段XY的中點.

有意思的是,直到1972年以前,人們對蝴蝶定理的證明都并非初等且十分繁瑣.至于初等數學的證法,在國外出現的資料中,一般都認為是由一位中學教師斯特溫首先給出的面積法證明.1985年,在河南省《數學教師》創刊號上,杜錫錄(1941～1994)教授以《平面幾何中的名題及其妙解》為題,載文向國內介紹蝴蝶定理,從此蝴蝶定理在神州大地到處傳開.

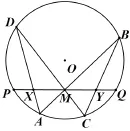
圖25

下面介紹一種較為簡便的初等證法：

如圖26所示,作OS⊥AD于 S,OT⊥BC 于 T,連 結OX,OY,MS,MT,OM.

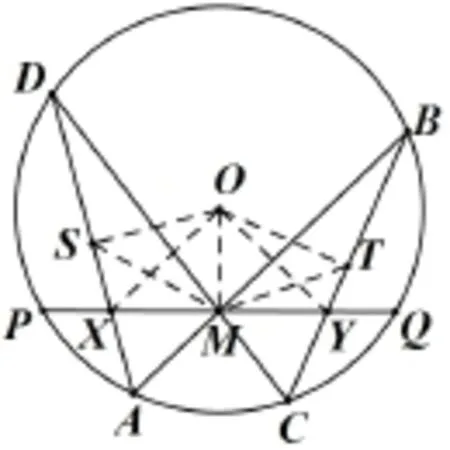
圖26

再由M是弦PQ的中點,可得OM⊥XY,所以M為線段XY的中點.

實際上,還可把蝴蝶定理推廣到任意的圓錐曲線中：

若過圓錐曲線Γ的弦AB的中點M 任作兩條弦CD,EF,直線CE,DF與直線AB分別交于點P,Q,則|MP|=|MQ|.

證明如圖 27所示,以M為坐標原點,直線AB為y軸,建立平面直角坐標系xMy.

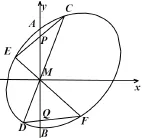
圖27

可設圓錐曲線Γ的方程為ax2+bxy+cy2+dx+ey+f=0.再設A(0,t),B(0,-t)(t＞0),得t,-t是關于y的方程cy2+ey+f=0的兩個根,所以c/=0,e=0.

當直線CD,EF的斜率有不存在的情形時,可得欲證結論成立.

1.7 楊輝三角

題目24 (2006年高考湖北卷理科第15題)將楊輝三角中的每一個數都換成,就得到一個如圖28所示的分數三角形,成為萊布尼茨三角形,從萊布尼茨三角形可看出,其.

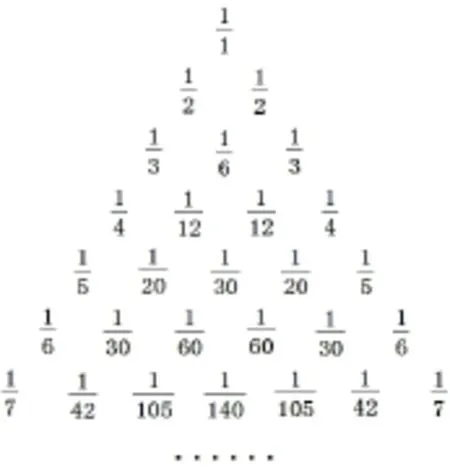
圖28

答案.

評析顯然該題有數學史背景,萊布尼茨(Gottfriend WilhelmvonLeibniz,1646～1716)是德國數學家、哲學家,同英國數學家、物理學家、天文學家牛頓并稱為微積分學的創始人,他所創造的微分和積分符號一直沿用至今.楊輝是中國南宋末年的一位杰出數學家、數學教育家,楊輝三角是楊輝(?～1298)的一大重要研究成果,它的許多性質與組合數的性質有關,楊輝三角中蘊含了許多優美的規律.而高中生對這些大數學家應當有所了解.

本題重在考查考生的觀察能力和用等價轉化思想解題.

題目25 (2007年高考湖南卷理科第15題)將楊輝三角中的奇數換成1,偶數換成0,得到如圖29所示的0-1三角數表.從上往下數,第1次全行的數都為1的是第1行,第2次全行的數都為1的是第3行,...,第n次全行的數都為1的是第___行;第61行中1的個數是____.

圖29

解2n-1,32.

由不完全歸納法知,全行都為1的是第2n-1行;因為26-1=63,所以第63行共有64個1,逆推知第62行共有32個1,并且是101010···01(共63個數)的形式(也可用不完全歸納法),再歸納出第61行是11001100···110011(共62個數)的形式,知共有32個1.

評析本題難度較大,考查不完全歸納法.要想徹底弄清每個組合數的奇偶性是很困難的.

題目26 (2004上海春季高考第11題)如圖30,在由二項式系數所構成的楊輝三角形中,第____行中從左至右第14與第15個數的比為2:3.

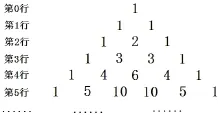
圖30

答案34.

1.8 多邊形數

題目27 (2009年高考湖北卷文科、理科第10題)古希臘人常用小石子在沙灘上擺成各種形狀來研究數.比如：

圖31

圖32

他們研究過圖31中的1,3,6,10,···,由于這些數能夠表示成三角形,將其稱為三角形數;類似的,稱圖32中的1,4,9,16,···這樣的數為正方形數.下列數中既是三角形數又是正方形數的是( )

A.289 B. 1024 C.1225 D. 1378

答案C.

題目28 (2012年高考湖北卷文科第17題)傳說古希臘畢達哥拉斯學派的數學家經常在沙灘上畫點或用小石子表示數.他們研究過如圖31所示的三角形數：

將三角形數1,3,6,10,···記為數列{an},將可被5整除的三角形數按從小到大的順序組成一個新數列{bn}.可以推測：

(1)b2012是數列{an}中的第____項;

(2)b2k-1=____.(用k表示)

答案(1)5030;(2).

題目29 (2013年高考湖北卷理科第14題)古希臘畢達哥拉斯學派的數學家研究過各種多邊形數,如三角形數1,3,6,10,···,第n個三角形數為.記第n個k邊形數為N(n,k)(k≥3),以下列出了部分k邊形數中第n個數的表達式：

六邊形數N(n,6)=2n2-n,

······

可 以 推 測 N(n,k)的 表 達 式,由 此 計 算N(10,24)=___.

答案1000.

評析這三道高考題都涉及古希臘人研究過的多邊形數.且題目27、題目28均源于普通高中課程標準實驗教科書《數學5·必修·A版》(人民教育出版社,2007年第3版)(下簡稱《必修5》)第28頁.題28和題29主要考查考生的觀察、猜想、驗證的解題能力.

小學生也可解答題27這道選擇壓軸題：只需考查m2(m∈N?)及1+2+···+n=n(n+1)(n∈N?)的2倍n(n+1)的個位數字便可用排除法求解.

若解答此題的一般情形,還需要用到不定方程中的佩爾方程[3]知識.

1.9 祖暅原理

題目30 (2013年高考上海卷理科第13題)在xOy平面上,將兩個半圓弧(x-1)2+y2= 1(x≥1)和(x-3)2+y2=1(x≥ 3)、兩條直線y=1和y=-1圍成的封閉圖形記為D,如圖33中陰影部分.記D繞y軸旋轉一周而成的幾何體為Ω,過(0,y)(|y|≤1)作Ω的水平截面,所得截面面積為4π,試利用祖暅原理、一個平放的圓柱和一個長方體,得出Ω的體積值為____

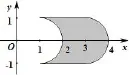
圖33

解2π2+16π.由幾何體為Ω的水平截面面積為,它由兩部分組成.

由祖暅原理可得,幾何體Ω中對應部分的體積就是該圓柱體的體積,即2π2.

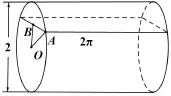
圖34

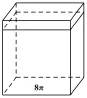
圖35

第二部分為定值8π.如圖35所示,圖35表示底面積為8π、高為2的長方體(其體積為8π·2=16π).由祖暅原理可得,幾何體Ω中對應部分的體積就是該長方體的體積,即16π.所以幾何體Ω的體積為2π2+16π.

評析祖暅 (公元前 5～6世紀),字景爍,祖沖之(429～500)之子,范陽郡薊縣(今河北省淶源縣)人,南北朝時代偉大的科學家.他繼承劉徽(約225～295)和祖沖之的工作,解決了球體積的計算問題,與其父共著《綴術》.在天文學方面,曾測量日影長度,發現北極星與北天極不動處相差一度有余,糾正了北極星就是北天極不動處的錯誤觀點.主要著作有《漏刻經》一卷、《天文錄》三十卷(均已失傳).

祖暅在數學上的突出貢獻是他在實踐的基礎上,于5世紀末提出體積計算原理(祖暅原理)：“冪勢既同,則積不容異”.“勢”即是高,“冪”是面積.意思是,如果兩等高的幾何體在同高處截得兩幾何體的截面積恒等,那么這兩個幾何體的體積相等.祖暅提出上面的原理,要比其他國家的數學家早一千多年.在歐洲直到17世紀,才有意大利數學家卡瓦列利提出上述結論.(見《必修2》第30-31頁.)

1.10 錯位數

題目31 (1)(2004年高考湖北卷文科第11題)將標號為1,2,···,10的10個球放入標號為1,2,···,10的10個盒子里,每個盒內放一個球,恰好3個球的標號與其在盒子的標號不一致的放入方法種數為( )

A. 120 B. 240 C. 360 D. 720

(2)(2004年高考湖北卷理科第 14題)將標號為1,2,···,10的10個球放入標號為1,2,···,10的10個盒子內,每個盒內放一個球,則恰好有3個球的標號與其所在盒子的標號不一致的放入方法共有____種.(以數字作答)

答案(1)B.(2)240.

評析這兩道小題實質相同,背景都是“錯位數”[4](數學家歐拉和丹尼爾·伯努利(DanielBernoulli,1700～1782)都研究過錯位數).記n個元素的錯位數為Dn,可得D1=0,D2=1,D3=2,D4=9.這兩道題有相同的解法：.

1.11 歐拉公式

題目32 (2014年高考陜西卷理科第14題)觀察分析下表中的數據：

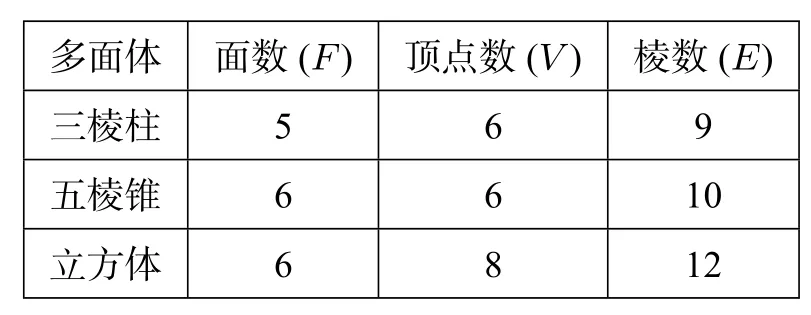
多面體面數(F)頂點數(V)棱數(E)三棱柱5 6 9五棱錐6 6 10立方體6 8 12

猜想一般凸多面體中F,V,E所滿足的等式是___.

答案F+V-E=2.

評析本題考查合情推理中的歸納.歐拉是瑞士數學家、自然科學家.生于瑞士的巴塞爾,在俄國圣彼得堡去逝.13歲時入巴塞爾大學學習,是約翰·伯努利(JohannBernoulli, 1667～1748)的學生,15歲大學畢業,16歲獲得碩士學位.歐拉是18世紀數學界最杰出的人物之一,他不但為數學界作出貢獻,更把整個數學推至物理的領域.他是數學史上最多產的數學家,平均每年寫出八百多頁的論文,還寫了大量的力學、分析學、幾何學、變分法等的課本,《無窮小分析引論》《微分學原理》《積分學原理》等都成為數學界中的經典著作.歐拉對數學的研究如此之廣泛,因此在許多數學的分支中也可經常見到以他的名字命名的重要常數、公式和定理.此外,歐拉還涉及建筑學、彈道學、航海學等領域.瑞士教育與研究國務秘書CharlesKleiber曾表示：“沒有歐拉的眾多科學發現,今天的我們將過著完全不一樣的生活.”法國數學家拉普拉斯(Pierre-SimonLaplace,1749～1827)則認為：讀讀歐拉,他是所有人的老師.

1.12 割圓術

題目33 (2010年高考湖北卷理科第7題)如圖36所示,在半徑為r的圓內作內接正六邊形,再作正六邊形的內切圓,又在此內切圓內作內接正六邊形,如此無限繼續下去.設Sn為前n個圓的面積之和,則=( ) A. 6πr2B. 4πr2C.D. 2πr2

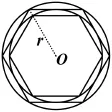
圖36

圖37

答案B.

評析此題有中國古代數學家劉徽(約225～約295)的割圓術這一數學史(如圖37所示)的背景.

劉徽的一生是為數學刻苦探求的一生.他終生未曾做官,故稱為“布衣”;但他人格高尚,治學嚴謹,堪稱楷模,萬世師表.他不是沽名釣譽的庸人,而是學而不厭的偉人,他給我們中華民族留下了寶貴的財富,不愧是中國古代一位杰出的布衣數學大師[5].

本題考查的知識是求等比數列的前n項和及數列極限.

《必修3》第45-47頁介紹了割圓術.

1.13 皮克公式

題目34 (2013年高考湖北卷文科第17題)在平面直角坐標系中,若點P(x,y)的坐標x,y均為整數,則稱點P為格點.若一個多邊形的頂點全是格點,則稱該多邊形為格點多邊形.格點多邊形的面積記為S,其內部的格點數記為N,邊界上的格點數記為L.例如圖38中△ABC是格點三角形,對應的S=1,N=0,L=4.

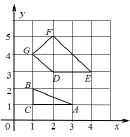
圖38

(1)圖中格點四邊形DEFG對應的S,N,L分別是___;

(2)已知格點多邊形的面積可表示為S=aN+bL+c,其中a,b,c為常數,若某格點多邊形對應的N=71,L=18,則S=____.(用數值作答.)

答案(1)3,1,6.(2)79.

評析本題的背景是皮克(GeorgePick,1859～1943,奧地利數學家)公式：頂點是整點(橫坐標、縱坐標均是整數的點叫做整點)的多邊形(可以是凸多邊形也可以是凹多邊形)的面積是S=a+-1,其中a表示多邊形內部的點數,b表示多邊形邊界上的點數.

題目35(2014年高考湖北卷第理科21題)(2014年高考湖北卷文科第22題)π為圓周率,e=2.71828···為自然對數的底數.

(2)(文)求e3,3e,eπ,πe,3π,π3這6個數中的最大數與最小數.

(理)將e3,3e,eπ,πe,3π,π3這6個數按從小到大的順序排列,并證明你的結論.

答案(1)增區間為(0,e),減區間為(e,+∞).

(2)(文)所求最大數與最小數分別是3π,3e.

(理)3π＞π3＞eπ＞πe＞e3＞3e.

評析第(1)問是經典問題,2013年高考北京卷理科第18題、1983高考全國卷理科第九題、2005年高考全國卷III理科第6題、2001年高考全國卷理科第20題都與此函數有關,由此函數的單調區間可得經典問題“比較ab與ba的大小”的簡潔結論：

(1)當0＜a＜b≤e時,ab＜ba;

(2)當e≤a＜b時,ab＞ba;

(3)當-0＜a≤1且a＜b時,ab＜ba;

(4)當1＜a＜e且b＞e時,ab＜ba,ab=ba,ab＞ba均有可能.

另外,該題中的六個冪涉及數學中的兩個重要常數e和π(e＜3＜π),所以本題“美麗無比”.

題目36 (1)(2015年高考安徽卷文科第7題)執行如圖39所示的程序框圖(算法流程圖),輸出的n為( )

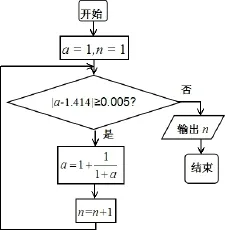
圖39

A. 3 B. 4 C. 5 D. 6

(2)(2015年高考安徽卷理科第13題)執行如圖39所示的程序框圖(算法流程圖),輸出的n為____.

答案(1)B.(2)4.

評析本題的背景是人類歷史是發現的第一個無理數即的無限連分數的前四個漸進分數.

1.15 阿基米德三角形

題目37 (2015年高考全國卷I理科第20題)在直角坐標系xOy中,曲線C:與直線l:y=kx+a(a＞0)交于M,N兩點. (1)當k=0時,分別求C在點M和N處的切線方程; (2)y軸上是否存在點 P,使得當 k變動時,總有∠OPM=∠OPN?說明理由.

答案(1)和.(2)存在點P(0,-a)符合題意.

題目38 (2007年高考江蘇卷第19題)如圖40,在平面直角坐標系xOy中,過y軸正方向上一點C(0,c)任作一直線,與拋物線y=x2相交于A,B兩點.一條垂直于x軸的直線,分別與線段AB和直線l:y=-c交于點P,Q.

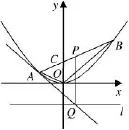
圖40

(2)若P為線段AB的中點,求證：QA為此拋物線的切線;

(3)試問(2)的逆命題是否成立?說明理由.

答案(1)c=2.(2)略.(3)(2)的逆命題成立,理由略.

題目39 (2006年高考全國卷II理科第21題)已知拋物線x2=4y的焦點為F,A、B是拋物線上的兩動點,且(λ＞0).過A、B兩點分別作拋物線的切線,設其交點為M.

(2)設△ABM的面積為S,寫出S=f(λ)的表達式,并求S的最小值.

答案(1).(2),S的最小值是4.

題目40 (2005年高考江西卷理科第22題)如圖41,設拋物線C:y=x3的焦點為F,動點P在直線l:x-y-2=0上運動,過P作拋物線C的兩條切線PA、PB,且與拋物線C分別相切于A、B兩點.

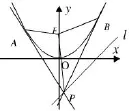
圖41

(1)求△APB的重心G的軌跡方程;

(2)證明∠PFA=∠PFB.

答案(1)3y=4x2-x+2.(2)略.

評析題37～40的背景都是阿基米德三角形(拋物線的弦與該拋物線在該弦的端點處的兩條切線圍成的三角形叫做阿基米德三角形).阿基米德最早利用逼近思想證得了結論：拋物線的弦與拋物線圍成的封閉圖形的面積是相應的阿基米德三角形面積的.阿基米德三角形的眾多性質是編制高考試題的源泉,讀者可參見文獻[6]-[9].

1.16 方格幾何學

題目41 (2014年高考福建卷文科第12題)在平面直角坐標系中,兩點P1(x1,y1),P2(x2,y2)間的“L-距離”定義為||P1P2||=|x1-x2|+|y1-y2|,則平面內與x軸上兩個不同的定點F1,F2的“L-距離”之和等于定值(大于||F1F2||)的點的軌跡可以是( )

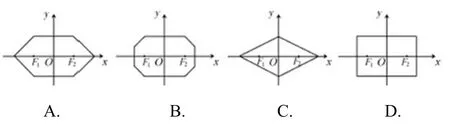
答案A.

題目42 (2006年高考福建卷理科第12題)對于直角坐標平面內的任意兩點A(x1,y1),B(x2,y2),定義它們之間的一種“距離”：||AB||=|x1-x2|+|y1-y2|.

給出下列三個命題：

①若點C在線段AB上,則||AC||+||CB||=||AB||;

②在△ABC中,若∠C=90°,則||AC||2+||CB||2= ||AB||2;

③在△ABC中,||AC||+||CB||＞||AB||.

其中真命題的個數為( )

A.0 B.1 C.2 D.3

答案B.(①正確)

題目43 (2010年高考廣東卷理科第 21題)設A(x1,y1),B(x2,y2)是平面直角坐標系xOy上的兩點,現定義由點A到點B的一種折線距離ρ(A,B)為ρ(A,B)= |x1-x2|+|y1-y2|,對于平面xOy上給定的不同的兩點A(x1,y1),B(x2,y2)：

(1)若點C(x,y)是平面xOy上的點,試證明ρ(A,C)+ ρ(C,B)≥ρ(A,B);

(2)在平面 xOy上是否存在點 C(x,y),同時滿足：quan1ρ(A,C)+ρ(C,B)= ρ(A,B);②ρ(A,C)= ρ(C,B).若存在,請求出所有符合條件的點;若不存在,請予以證明.

答案(2)存在,即線段AB的中點.

評析題目41～43的背景都是方格幾何學.方格幾何學是由生于俄國的著名德籍數學家閔可夫斯基(Hermann Minkowski,1864～1909)最先開始研究的.文獻[10]簡單介紹了方格幾何學.

[1]張奠宙.多一點數學文化的考題[J].數學教學,2015(9)：封底

[2]甘志國.高考壓軸題(上)[M].哈爾濱：哈爾濱工業大學出版社, 2015.28-29

[3]甘志國.湖北高考數學卷與世界名題相通[J].數學教學,2009(11)：46-48

[4]甘志國.為2010年的高考數學湖北卷叫好[J].數學通訊,2010(8下)：46-50

[5]甘志國.中國古代杰出的布衣數學大師劉徽[J].新高考(高一·數學(必修1)),2016(10)：14-15

[6]殷加興.阿基米德三角形初探[J].中學數學研究(江西),2009(12)4頁

[7]邵明志,陳克勤.高考試題中的阿基米德三角形[J].數學通報, 2008(9)

[8]王學鳳,劉曉銳.悄然興起的阿基米德三角形[J].高中數學教與學, 2009(5)

[9]丁益民.一道高考試題引發的探究與思考[J].數學通訊,2010(10下)

[10]甘志國.有趣的方格幾何[J].新高考(高二·數學),2013(11)：39-40

*該文為連載文章,共有三個部分,這是其中的第II部分—編者注.