探究食物網中食物鏈的數量

郭進宏

食物鏈和食物網的相關概念及數量計算，出現在人教版高中生物教材必修III中第五章第一節中。是高考必考的內容。探究食物鏈的數量問題，是對于食物網相關的考查首先要解決的問題，有利于學生較快把握題目的結構，準確解答相關問題，也有利于教師有效地教學。

食物鏈食物網數量

一、引言

隨著新一輪高考改革的進行，對于學生的學習能力有了更深層次的要求，特別是對于探究能力、解決實際情況的能力的考查。探究食物鏈的數量，是解決有關生態系統的穩定性、物質循環、能量流動、信息傳遞的先決條件。在實際的教學中，因為沒有相關的、系統的食物鏈數量的教學方法，使教師及學生在教學此問題時，往往會因為疏忽而導致食物鏈數量的錯誤，進而影響后續的解題。本課題正是結合多年的教學經驗及高考的考查，總結出相關的方法。

二、探究食物鏈的數量

方法一：傳統的路徑法

以第一營養級為起點，以最高營養級為終點，注意每條路徑上的分岔點。

例1.2014江蘇卷。如圖，食物鏈有8條。

食物鏈1：甲→乙→辛；

食物鏈2：甲→乙→丁→辛；

食物鏈3：甲→丙→乙→辛；

食物鏈4：甲→丙→乙→丁→辛；

食物鏈5：甲→丙→丁→辛；

食物鏈6：甲→丙→已→庚；

食物鏈7：戊→丁→辛；

食物鏈8：戊→已→庚。

方法二：樹狀圖法

以第一營養級為起點，最高營養級為終點，每種捕食關系對應一條分支。最高營養級出現的次數即為食物鏈的條數。

識圖可知，辛和庚作為最高營養級在食物鏈的結尾共出現8次，即8條食物鏈。

從圖中，可知，同一列為同一營養級，第幾列即為第幾營養級。同時，可反映出，同一種生物可處于不同營養級，如辛，可處于第三、第四、第五營養級。

方法三：計算法

第一營養級：在生態系統中，生產者只會被捕食，所以可描述為只出不進，0進n出，計n；最高營養級：同理，只進不出，m進0出，計0（因為在倒數第二營養已經計算在內）；其他營養級：X進Y出；Y-1代表此路徑已經被利用一次；X代表利用次數；Σ表示所有的集合求和。

例2.2011年新課標卷。如圖，食物鏈有4條。

如上題：第一營養級的牧草可被羊和兔食用，0進2出，計n=2；最高營養級的人，可捕食羊、兔、狐，3進0出，計0；其他營養級的羊，只能捕食牧草，但被人和狐捕食，1進2出，套用X羊（Y羊-1）=1（2-1）=1；同理，兔，X兔（Y兔-1）=1。求和：N=

對于有多個第一營養級的食物網，采用拆分法，把食物網拆分為相應數量的食物網后，分類討論后求和。拆分的依據為：凡是和某第一營養級相關的生物，全為同一食物網。

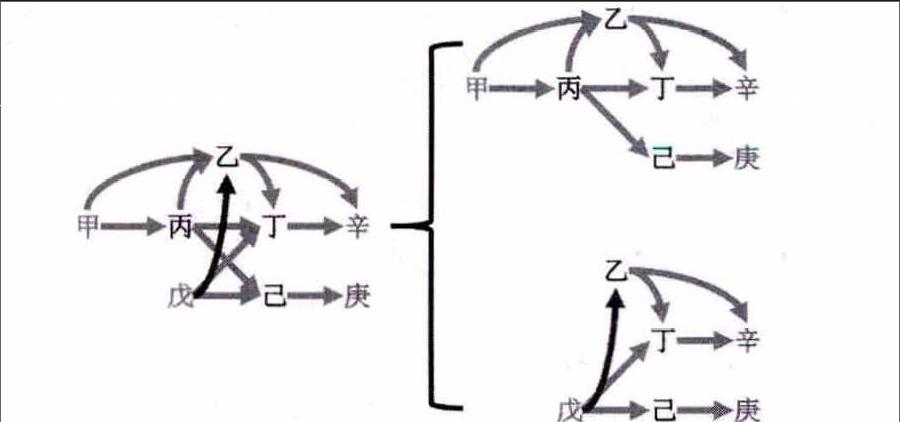
例3.2014江蘇卷改編。

由于此食物網中有兩個第一營養級，且乙同時捕食兩種第一營養級，對于此類食物網，必須先拆分為兩個食物網進行分類討論。

和甲相關的物種有乙、丙、丁、已、辛和庚；和戊相關的物種有乙、丁、已、辛和庚。分解為兩圖。

情況一：第一營養級的甲，0進2出，計2；最高營養級有辛和庚，總計3進0出，計0；其他營養級的乙，2進2出，所以X乙（Y乙-1）=2；其他營養級的丙，1進3出，所以X丙（Y丙-1）=2；其他營養級的丁，2進1出，所以X丁（Y丁-1）=0；其他營養級的乙，1進1出，所以X已（Y已-1）=0；N1=Σ{n}+Σ{X（Y-1）}=2+（2+2）=6

情況二：第一營養級有戊，0進3出，計3；最高營養級有辛和庚，總計3進0出，計0；其他營養級的乙，1進2出，所以X乙（Y乙-1）=1；其他營養級的丁，2進1出，所以X丁（Y丁-1）=0；其他營養級的已，1進1出，所以X已（Y-已1）=0；N2=Σ{n}+Σ{X（Y-1）}=3+1=4；∴N=N1+N2=10

三、解題規律

1.凡是X進1出的營養級，X（Y-1）=0。所以，在熟練之后，先確定并計算第一營養級，再排除最高營養級和X進1出的營養級。其他的逐個計算。

2.并不是所有的含有多個第一營養級的食物網都需要拆分，如上題，亦可不拆分。但為了方便學生理解和教學的深入淺出，在這里不討論多個營養級不拆分的情況。

四、結束語

食物鏈的數量問題是高考的必考內容，也是學生必須要掌握和應用的能力。以上討論的方法，有助于教師的教學和學生的學習。在實踐操作中，應就每種方法進行逐一的介紹，讓學生掌握每種方法的本質和內涵，進行對比，從而掌握應用。然后，根據題目要求，采用適合的方法，快速解答此類問題。

參考文獻：

＼[1＼]人民教育出版社、課程教材研究所、生物課程教材研究開發中心.普通高中課程標準實驗教科書·生物必修3·生態系統的結構.2016.88-92.