船舶砰擊載荷等效靜態方法數值分析

田喜民, 馬興磊, 朱青淳, 吳嘉蒙, 鄒早建

(1.上海交通大學 船舶海洋與建筑工程學院，上海 200240； 2.中國船舶及海洋工程設計研究院 上海市船舶工程重點實驗室，

船舶砰擊載荷等效靜態方法數值分析

田喜民, 馬興磊, 朱青淳, 吳嘉蒙, 鄒早建

(1.上海交通大學 船舶海洋與建筑工程學院，上海 200240； 2.中國船舶及海洋工程設計研究院 上海市船舶工程重點實驗室，

上海 200011； 3.中國船舶工業集團公司 規劃發展部，北京 100048)

由于砰擊載荷峰值較高，持續時間較短，因此在評估船體結構安全時需要對結構進行動力響應分析。本文對船體外板及骨材在瞬態砰擊載荷作用下的響應特性進行了研究，通過引入動態載荷因子(dynamic load factor, DLF)，將瞬態載荷轉化為靜態載荷。研究結果表明：當將砰擊載荷簡化為三角形脈沖載荷形式時，其作用時間接近于結構固有周期時結構動態回應最大，此時在工程設計時應考慮砰擊載荷動態效應的影響。

船體結構；砰擊載荷；動力回應；動態載荷因子；瞬態載荷；等效靜態方法

在船舶與海洋工程結構設計中，在滿足強度要求前提下，減輕結構重量是提高結構設計水平的關鍵。其中，靜強度設計方法已經基本成熟，其設計方法簡單、可靠，計算分析與試驗驗證都相對容易。但是，船體結構經常會遇到瞬態載荷的作用，如船體受到的波浪砰擊載荷，此時須對船體結構進行瞬態動力響應分析。對船體結構進行瞬態動力分析需要耗費大量的時間和精力，且計算結果受到較多參數的影響，計算過程不夠穩定。因此，若能得到砰擊載荷的等效靜態載荷，將等效靜態載荷作用于結構，分析得到與砰擊瞬態載荷作用相同的回應結果，將大大提高計算效率。

人們對砰擊載荷作用下結構的響應做了大量的研究，例如Jones等[1-5]預報了船體結構在砰擊載荷作用下的結構破壞問題，并在這方面提出了一些有用的觀點。Saitoh等[6]給出了鋼板在脈沖載荷作用下永久變形的經驗公式。Nurick等[7]對遭受脈沖載荷的方形薄板進行了試驗研究。Cheong等[8]對在流固沖擊載荷作用下矩形板的動力后屈曲特性進行了試驗研究。Wang等[9]采用直接計算方法研究了FPSO艏部抗砰擊設計。上述研究結果和方法為砰擊載荷作用下船體結構設計提供了一定的試驗和理論基礎，但是對于砰擊載荷作用下結構的等效靜態載荷研究的文獻較少。

實船及模型試驗都已表明，砰擊載荷具有局部性、瞬時性及壓力峰值沿船體表面快速移動三個主要特征[10]。如果按砰擊壓力的峰值對肋骨強度做靜力計算和設計的話，肋骨框架結構將會十分保守。文獻[10]中引入砰擊壓力“折減系數”的概念，將動態砰擊壓力轉化為與產生相同結構響應(應力)的等價均布靜壓力。“折減系數”量值反映了砰擊壓力的不均勻程度，可以看作主要是砰擊載荷在空間分布上的“折減”。本文暫時不對砰擊載荷在空間分布上的折減做研究。在對砰擊載荷在空間上“折減”前，應對結構在砰擊載荷作用下由于砰擊載荷的瞬態性引起的動載荷系數進行研究，Sinha等[11]對此進行了相關的研究。

本文基于文獻[12]的理論計算結果，對船體外板和舷側板架施加砰擊載荷，進行瞬態動力響應計算，分析結構在瞬態砰擊載荷作用下的響應，并與結構在砰擊載荷峰值作用下的靜態分析進行對比，從而得到砰擊載荷的等效靜態載荷。

1 砰擊載荷的計算

合理地預報砰擊載荷對船體結構設計和船舶航行安全至關重要。船底砰擊載荷峰值較高，作用時間較短，可能引起局部構件的破壞，嚴重者造成船體破艙，帶來不可估量的損失。與底部砰擊相比，外飄砰擊產生的水動力較小，作用面積較大，砰擊過程持續時間要長得多[12]。目前對砰擊載荷的預報一般有三種方法：1)基于水動力數值分析；2)基于試驗測量；3)基于經驗公式，例如船級社規范。

砰擊載荷可以用四個特征參數來表示： 1)起升時間直到砰擊壓力峰值；2)壓力峰值；3)壓力衰減形式；4)壓力作用時間，如圖1所示。

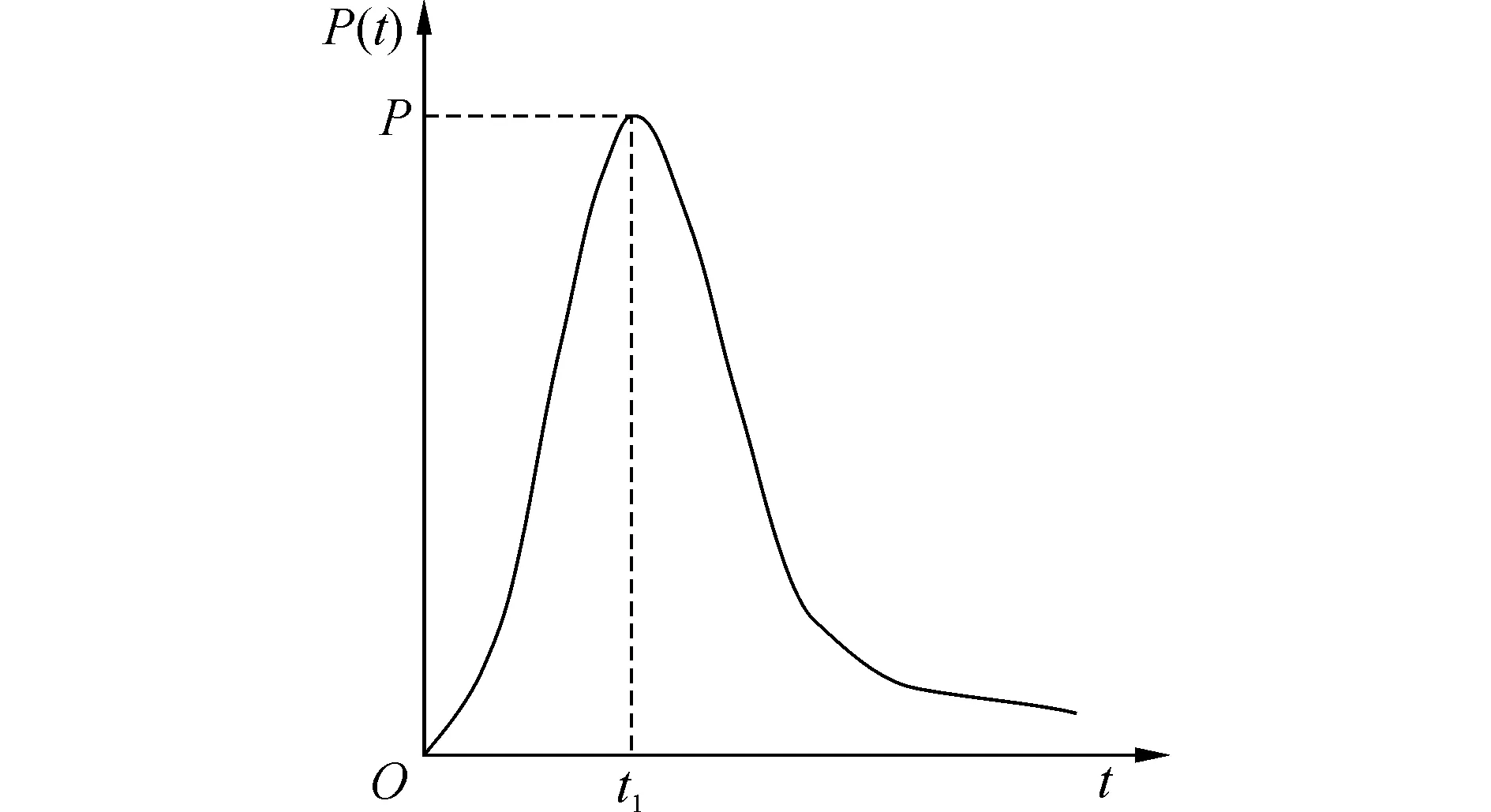
圖1 典型砰擊載荷壓力時間歷程曲線Fig. 1 Time history of typical slamming pressure

2 等效靜態載荷原理

等效靜態載荷原理可表述為：線性靜態分析中的結構等效靜態載荷能夠產生與對應時刻結構非線性動力學分析完全相同的系統響應場[13]。圖2給出了靜態載荷的等效過程。由圖可見，動力學分析中總的計算時間步為n+1步，在等效時，將每個計算時間步等效為靜態分析的一個工況，并且要求由第si個等效靜態載荷計算得到的系統響應等價于對應時間步的動態響應。因而，動力學分析中總的時間步數等于線性靜態分析中總的工況數。同樣，基于等效靜態載荷計算的結構線性靜態響應的包絡線與非線性結構動態響應的包絡線一致。根據這一原理可以求得對應于動力學分析每一時間步的每個靜態工況的等效靜態載荷feq0、feq1、feq2、…、feqn。

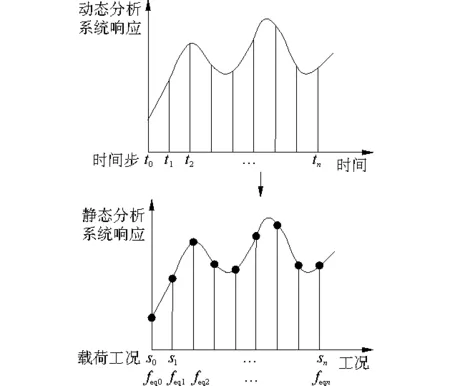
圖2 靜態載荷的等效過程Fig.2 Equivalent process of static loads

完全采用上述等效靜態載荷原理對砰擊載荷作用下船體結構強度進行評估，也將耗費大量的時間和精力，因此工程上廣泛采用的做法是將動載荷簡單處理為乘以動態載荷因子的靜載荷，動態載荷因子由設計規范或工程師的經驗決定。下面通過理論分析得到動態載荷因子。

在進行結構瞬態動力響應分析時，通過運用數值積分方法求解耦合方程。非線性動力學微分方程為

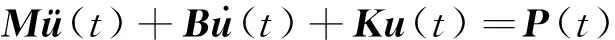
(1)

式中：M、B、K分別為動態質量矩陣、動態阻尼矩陣和動態剛度矩陣，P(t)表示t時刻外載荷列陣，u(t)為位移向量。

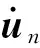
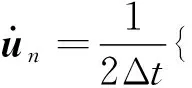
外力取3個鄰近時間點的平均值，得到運動方程:

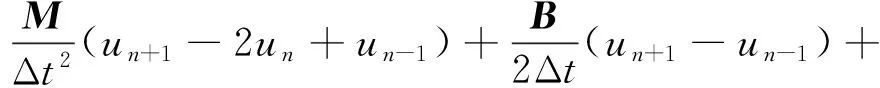
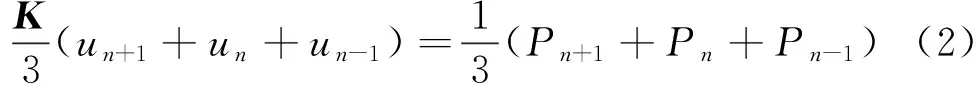
合并同類項，運動方程寫為

A1{un+1}=A2+A3{un}+A4{un-1}

(3)

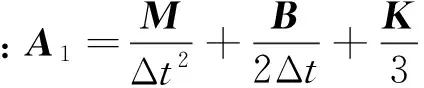
本文材料采用理想彈塑性材料模型，材料參數如下：楊氏彈性模量E為2.06×1011N/m2，泊松比γ為0.3，密度ρ為7 850kg/m3，屈服極限σs為355MPa。

3 動態載荷因子計算

砰擊載荷的等效靜態載荷可以通過砰擊載荷峰值乘以動態載荷因子(CDLF)得到。動態載荷因子與砰擊載荷作用時間t1和結構固有周期T(一階振動模態)的比值有關。在相同的砰擊載荷峰值Pm和不同t1/T比值作用下，本文通過一系列的非線性瞬態動力分析，得到結構的最大應力或變形。將瞬態得到的結構最大應力或變形與靜態非線性分析值比較，得到動態載荷因子CDLF：

CDLF=σd/σs或CDLF=wd/ws

(4)

式中：σd和σs分別為動態載荷和靜態載荷作用下結構的Von-mises應力，wd和ws分別為動態載荷和靜態載荷作用下結構的變形。

3.1 船體板動態載荷因子計算及分析

波浪砰擊載荷通常作用在一個較大的局部范圍內，因此可將砰擊載荷視為均布載荷。此外，作為船舶板周界的支撐結構，如縱桁、縱骨、肋骨及肋板等，其剛度遠大于船體板的剛度，因此可將船體板視為四邊固支的矩形板[14]。

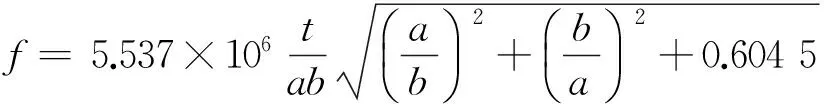
(5)

(6)

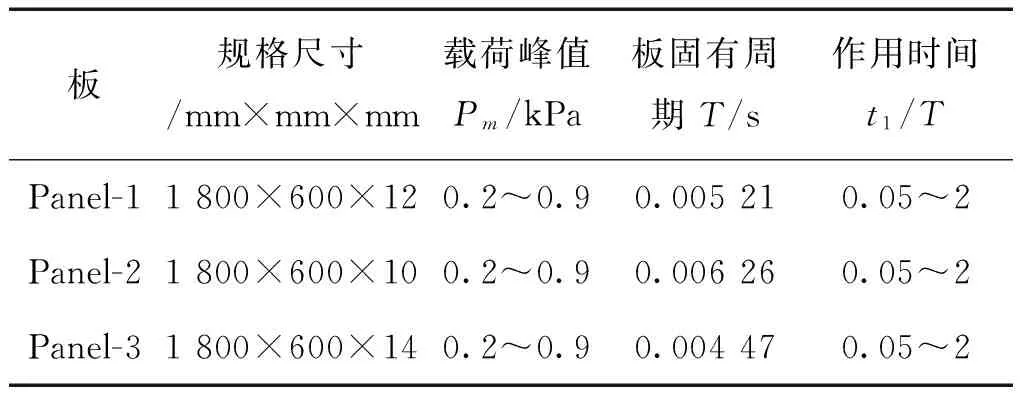
表1 板規格及相關參數Table 1 Parameters of panel plates

對于板Panel-1，對其加載靜態載荷時，其回應如表3所示。從表2中可以看出，當靜態載荷大于0.4 MPa時，板將進入塑性階段。

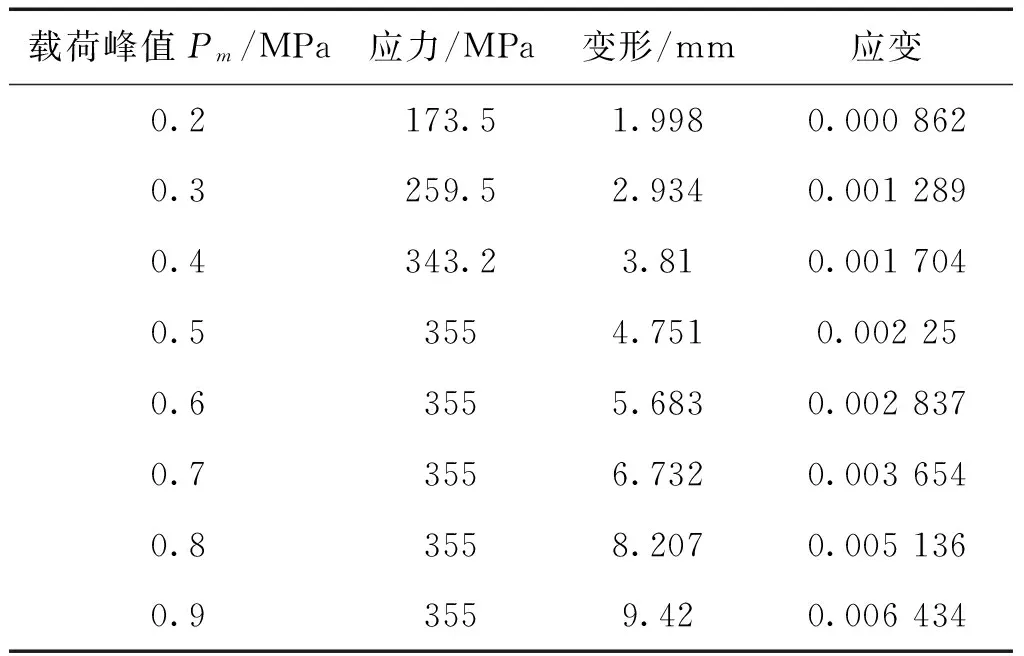
表2 Panel-1靜態載荷計算結果

對板Panel-1施加如圖3所示的瞬態載荷，當峰值載荷不小于0.3 MPa時，t1/T=0.2，0.4時板進入塑性階段，如表3所示。表3中給出了板遭受瞬態載荷時的應力、變形和應變值。圖4給出了板Panel-1在t1/T=0.8和Pm=0.3 MPa時其長邊中點處Von-mises應力的時歷變化曲線。

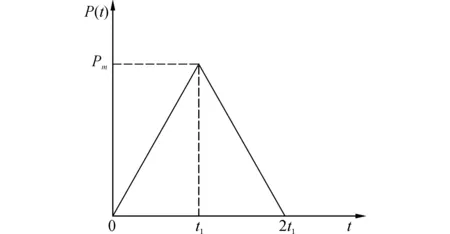
圖3 理想化砰擊載荷壓力時間歷程曲線Fig. 3 Idealized time curve of slamming pressure

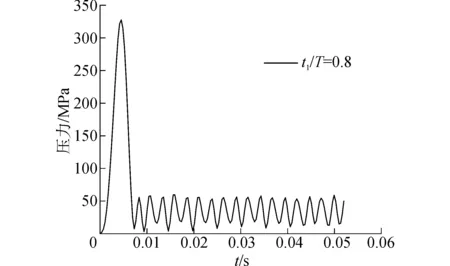
圖4 Pm=0.3 MPa時Panel-1應力變化Fig. 4 Variation of von-mises stress of Panel-1 at Pm=0.3 MPa

在各載荷峰值和t1/T工況下，動態載荷因子如圖5所示，圖中CDLF-deflection和CDLF-strain分別為采用變形和應變作為計算參數時對應的動態載荷因子，NSR為英國勞氏軍船規范[15]砰擊載荷動態載荷因子。從這些圖中可以看出，當板的應力大于屈服極限時，即板進入塑性階段時，計算其動態載荷因子時應使用變形或應變作為計算參數；從計算結果來看，選取變形作為計算參數所得動態載荷因子與勞氏軍船規范較接近，使用應變作為計算參數的結果偏于安全。

按照式(4)計算動態載荷因子，得到Panel-1、Panel-2、Panel-3在不同峰值下的動態載荷因子，如圖6所示。

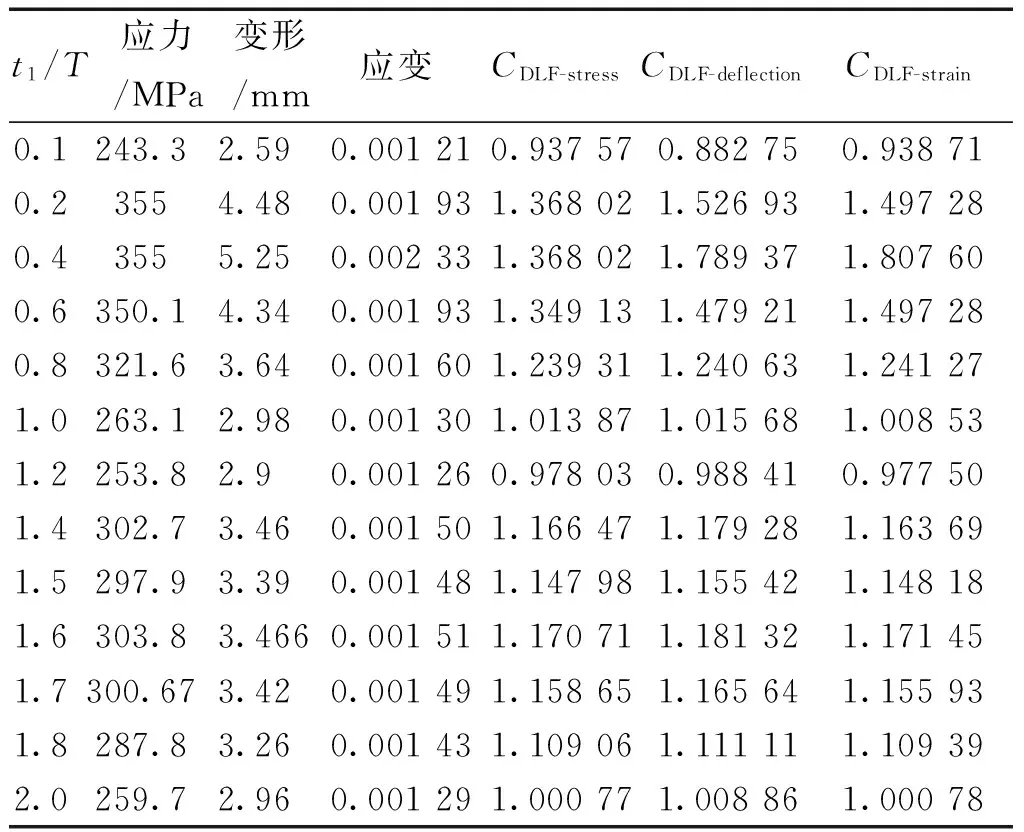
表3 Pm=0.3 MPa時瞬態動力分析計算結果

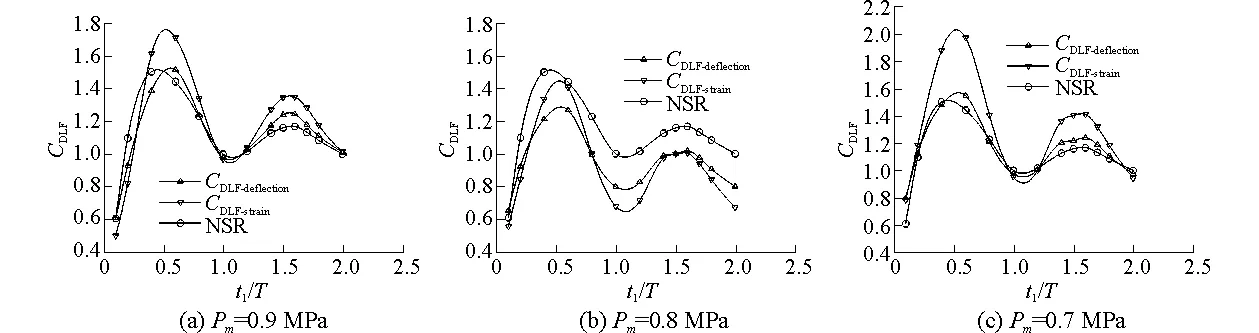
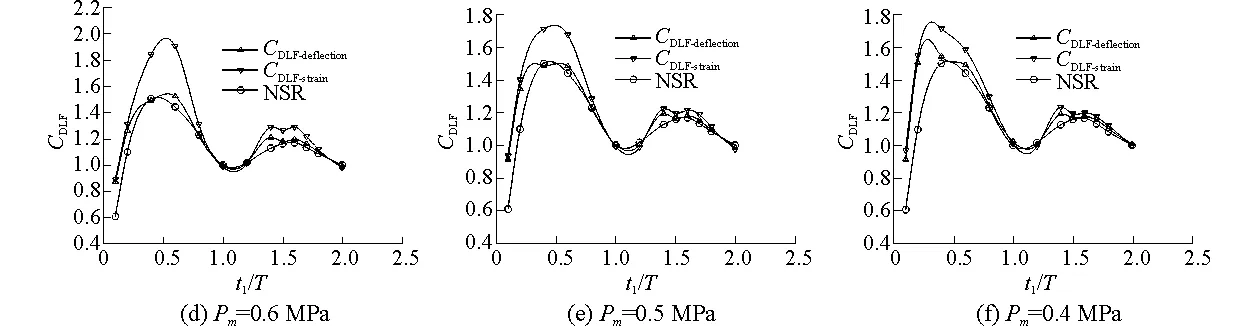
圖5 不同砰擊載荷作用下動態載荷因子Fig. 5 The DLF under different slamming loads

圖6 砰擊載荷作用下板動態載荷因子Fig. 6 The DLF of panel under slamming loads

由上述計算結果可以看出，當0.25≤t1/T≤0.9和1.25≤t1/T≤1.75時，需要對結構進行瞬態動力響應分析，尤其是t1/T在0.25～0.9時，動態效應較明顯。因此當0.25≤t1/T≤0.9和1.25≤t1/T≤1.75時，可以運用本文中的動態載荷因子對船體板進行靜態響應分析。

3.2 船體骨材動態載荷因子計算及分析

對于船體外板骨材，即舷側縱骨或舷側肋骨，可選取由骨材和外板組成的板架進行瞬態動力分析。其有限元模型如圖7所示，其骨材尺寸為HP240×12 mm，板厚為14 mm，強橫梁尺寸為⊥12×600/16×200 mm。

圖7 有限元模型Fig. 7 The finite element model

由于本文重點對骨材所受的動態載荷進行研究，因此施加的載荷范圍如圖8中陰影線所示，邊界條件為四周剛性固定。

通過對有限元模型進行模態分析，可得到縱骨及其帶板的一階垂向固有頻率為280 Hz，如圖9所示。因此，舷側縱骨一階垂向固有周期T取為0.003 6 s。

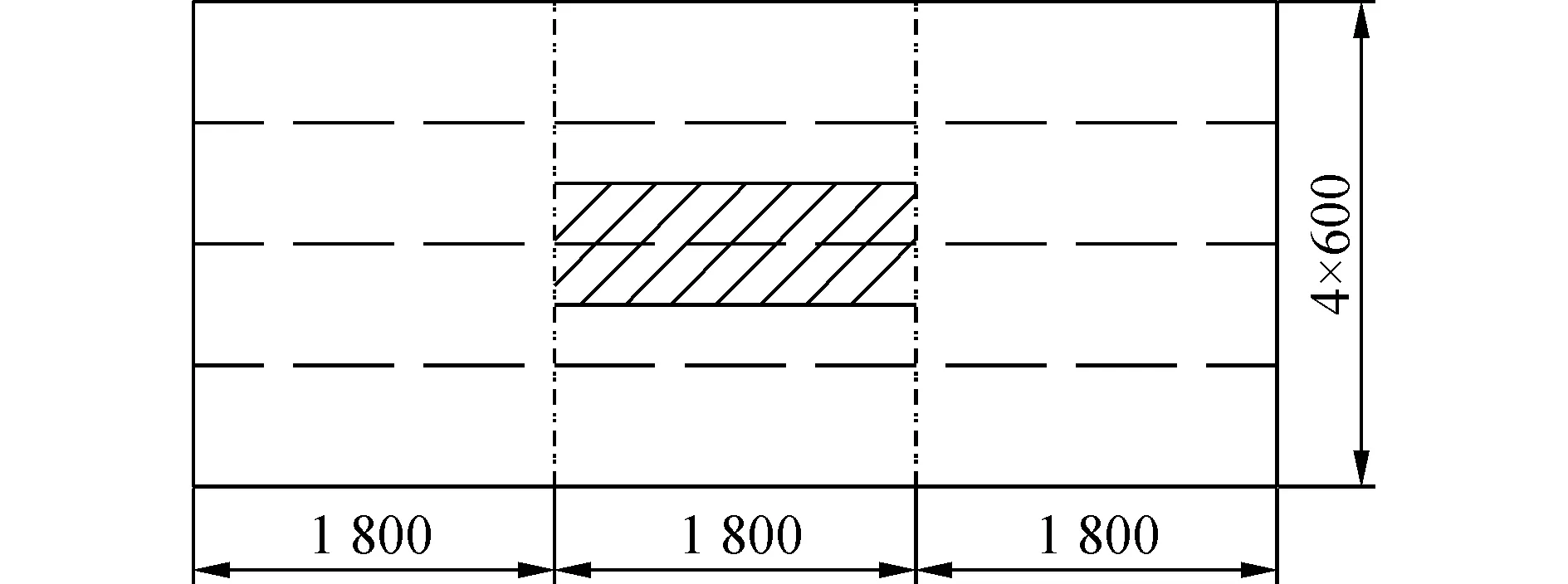
圖8 施加載荷范圍Fig. 8 The region of loads

對舷側縱骨施加0.9 MPa的靜態載荷，其靜態分析結果為應力325.3 MPa，變形6.823 mm，應變0.001 32。動態響應分析結果見表4，從表4中可以看出，當0.5≤t1/T≤1.2時，骨材進入塑性階段。

圖10給出了計算得到的船體骨材動態載荷因子，可以看出，船體骨材的動態載荷因子變化趨勢與勞氏規范有差異，這是因為所建模型為板架，計算其骨材固有周期時與實際值存在一定誤差，因此得到的動載荷存在一定誤差，但CDLF-Strain和勞氏規范均在t1/T=0.5附近動載荷系數達到最大。

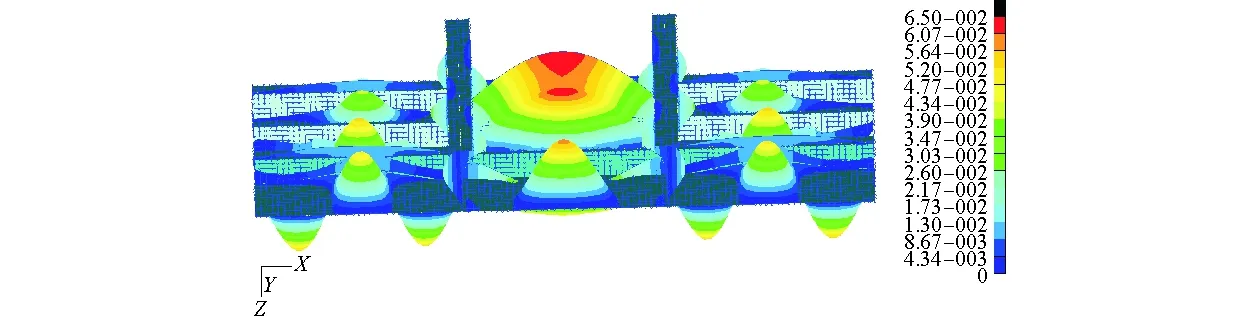
圖9 模態分析Fig. 9 The mode analysis

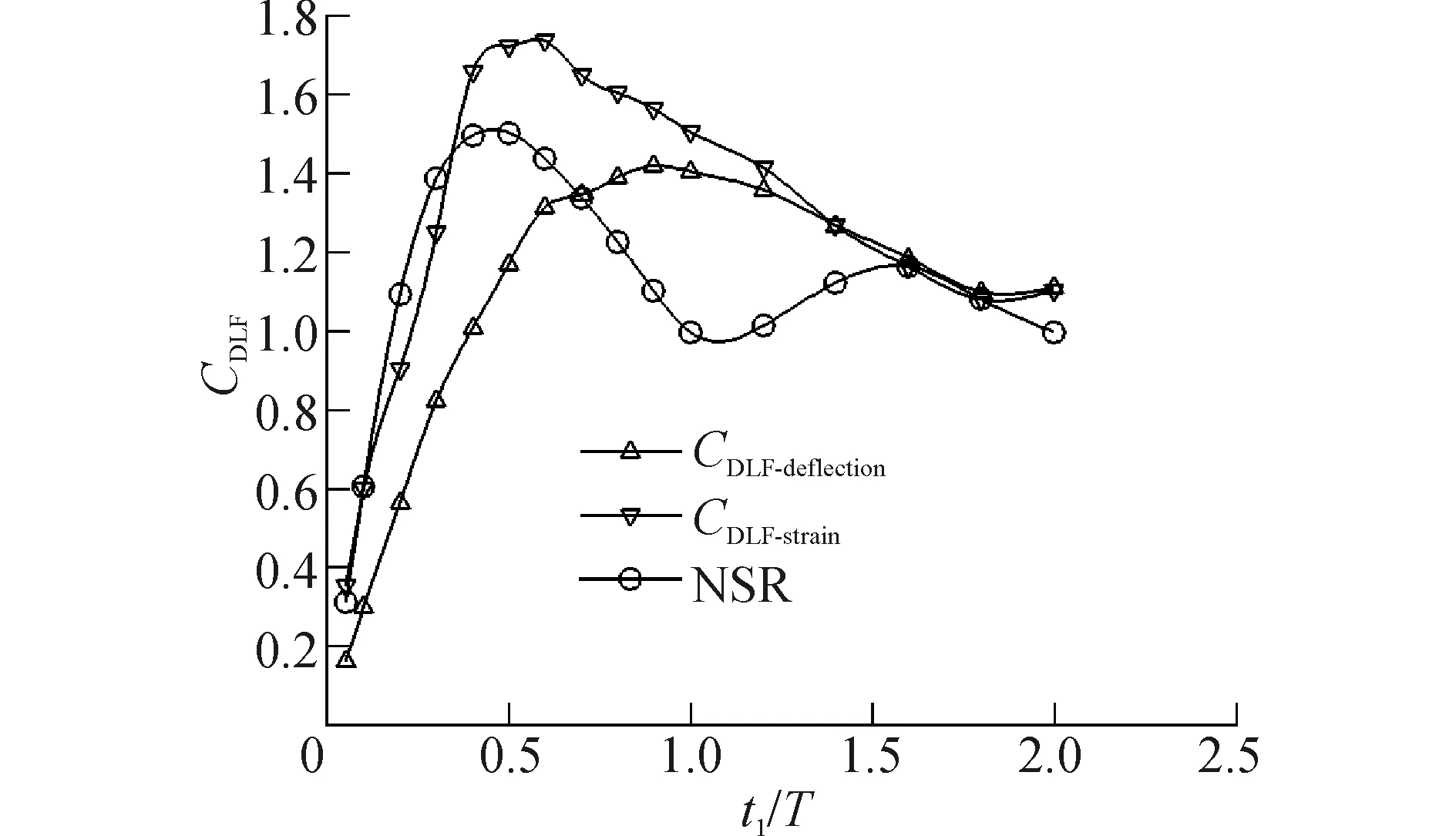
圖10 船體骨材動態載荷因子Fig. 10 The DLF of stiffener

表4 舷側縱骨瞬態動力分析計算結果

4 結論

本文應用非線性有限元方法，分別給出了船體外板和加筋板在砰擊載荷作用下結構的瞬態動力響應和靜態分析，得到了船體外板和骨材的動態載荷因子，并與勞氏規范[15]中動態載荷因子進行比較，驗證了本文方法的正確性。計算結果表明，當0.25≤t1/T≤0.9和1.25≤t1/T≤1.75時，需要對結構進行瞬態動力響應分析，尤其是t1/T在0.25～0.9時，動態效應較明顯。

一般而言，對于外飄砰擊，由于砰擊壓力較小，砰擊作用時間較長，因此其動態載荷系數較小，一般接近于1，實際計算時可以不考慮動態效應的影響。對于艏底砰擊，由于砰擊載荷較大，作用時間較短，且有附連水品質的影響，因此需要考慮動態效應的影響。

本文引入了動態載荷因子，給出了將瞬態載荷轉化為靜態載荷的方法和條件，可將復雜的瞬態動力分析轉化為靜態分析，為工程設計人員提供了一條可行且有效的技術途徑。

[1]JONES N. A theoretical study of the dynamic plastic behavior of beams and plates under finite-deflections[J]. International journal of solids and structures, 1971, (7): 1007-1029.

[2]JONES N. Slamming damage[J]. Journal of ship research, 1973, 17(2): 80-86.

[3]JONES N. Damage estimate for plating of ships and marine vehicles[C]. Proceedings of the International Symposium on Practical Design in Shipbuilding: PRADS’77, Tokyo, Japan, 1977, pp. 121-128.

[4]JONES N. Structural impact[M]. Cambridge University Press, Cambridge, UK, 1997.

[5]JONES N. Some recent developments in the dynamic inelastic behavior of structures[J]. Ships and offshore structures, 2006, 1(1): 37-42.

[6]SAITOH T, YOSHIKAWA T, YAO H. Estimation of deflection of steel panel under impulsive loading[J]. The Japan society of mechanical engineers, 1995, 61: 2241-2246.

[7]NURICK GN, SHAVE GC. The deformation and tearing of thin square plates subjected to impulsive loads—An experimental study[J]. International journal of impact engineering, 1996, 18(1): 99-116.

[8]CHEONG HK, HAO H, CUI S. Experimental investigation of dynamic post-buckling characteristics of rectangular plates under fluid-solid slamming[J]. Engineering structures, 2000, 22(8): 947-960.

[9]WANG G, TANG S, SHIN Y. A direct calculation approach for designing a ship-shaped FPSO’s bow against wave slamming load[C]. Proceedings of the 12thInternational Offshore and Polar Engineering Conference, Kitakyushu, Japan, 2002,IV:163-168.

[10]王輝. 船體結構局部強度設計中的砰擊載荷確定方法[J]. 中國造船，2010, 51(2)：68-77. WANG Hui. Slamming Load Determination in Local Structure Design of Ships[J]. Shipbuilding of China, 2010, 51(2): 68-77.

[11]SINHA S, KAR S, SARANGDHAR D G. Development of simplified structural design formulation for slamming loads[C]. Proceedings of the ASME 27thInternational Conference on Offshore Mechanics and Arctic Engineering, Estoril, Portugal, 2008.

[12]田喜民，鄒早建，王福花. 大型船舶外飄砰擊壓力研究[J]. 中國造船，2014, 55(1)：1-10. TIAN Ximin, ZOU Zaojian, WANG Fuhua. Numerical study on flare impact for large ships[J]. Shipbuilding of China, 2014, 55(1): 1-10.

[13]KANG B S, SHYY Y K, HONG Q. Implementation of Equivalent Static Load Method in Flexible Multibody Dynamic Systems[C]. 7thWorld Congress of Structural and Multidisciplinary Optimization, Seoul, Korea, 2007:21-25.

[14]陳鐵云，王德禹，黃震球. 船舶結構終極承載能力[M]. 上海：上海交通大學出版社，2005

[15]LLOYD’s Register. Rules and Regulations for the Classi-fication of Naval Ships[S]. January 2011.

Numerical analysis of ship slamming loads using the equivalent static method

TIAN Ximin1,2, MA Xinglei3, ZHU Qingchun2, WU Jiameng2, ZOU Zaojian1

(1. School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, China; 2. Shanghai Key Laboratory of Ship Engineering, Marine Design & Research Institute of China, Shanghai 200011, China; 3. Development Dept., China State Shipbuilding Corporation, Beijing 100048, China)

Owing to the high peak value and short duration of slamming loads, a dynamic response analysis is required during the assessment of the safety of a hull structure. In this paper, the response of a ship’s plate and stiffener under transient slamming loads was investigated. A dynamic load factor (DLF) was introduced to transform the transient slamming loads into equivalent static loads. The research results show that when the slamming load is simplified to a triangular impulsive load form and the duration of the slamming load is close to the structure’s natural period, the dynamic response reaches its maximum value. Therefore, the dynamic effect of slamming load should be taken into consideration in engineering design.

ship structure; slamming load; dynamic response; dynamic load factor (DLF); transient load; equivalent static method

2016-02-25.

日期：2017-03-02.

工信部高技術船舶科研專項項目(K24333).

田喜民(1981-)，男，高級工程師，博士研究生； 鄒早建(1956-)，男，教授，博士生導師.

鄒早建，E-mail：zjzou@sjtu.edu.cn.

10. 11990/jheu.201602029

U663

A

1006-7043(2017)03-0331-07

田喜民, 馬興磊, 朱青淳,等.船舶砰擊載荷等效靜態方法數值分析[J]. 哈爾濱工程大學學報, 2017, 38(3):331-337.

TIAN Ximin, MA Xinglei, ZHU Qingchun，et al. Numerical analysis of ship slamming loads using the equivalent static method[J]. Journal of Harbin Engineering University, 2017, 38(3):331-337.

網絡出版地址：http://kns.cnki.net/kcms/detail/23.1390.U.20170313.0924.006.html