微擾法聲速剖面反演改進算法

鄭廣贏, 黃益旺

(1.哈爾濱工程大學 水聲技術重點實驗室，黑龍江 哈爾濱 150001；2.哈爾濱工程大學 水聲工程學院，黑龍江 哈爾濱 150001)

微擾法聲速剖面反演改進算法

鄭廣贏, 黃益旺

(1.哈爾濱工程大學 水聲技術重點實驗室，黑龍江 哈爾濱 150001；2.哈爾濱工程大學 水聲工程學院，黑龍江 哈爾濱 150001)

為了降低傳播時間測量誤差對微擾法聲速剖面反演精度的影響，本文提出了一種基于微擾法的聲速剖面反演改進算法。該算法通過調整平均聲速剖面以增大聲速擾動量，進而增大聲速擾動所引起聲線傳播時間的擾動量，降低了測時誤差對反演算法的影響，提高了反演算法對聲速擾動的敏感性。數值算例表明，相同條件下傳統微擾法反演的聲速剖面的最大誤差為1.478 m/s，而改進算法的最大誤差降低至0.403 m/s，驗證了改進算法可以有效降低傳播時間測量誤差對聲速剖面反演結果的影響，比微擾法的反演精度更高。

聲速剖面；微擾法；反演；經驗正交函數(EOF)；聲線傳播時間；測時誤差

為了快速獲取大面積海域的聲速剖面信息，聲學反演方法得到了國內外學者的廣泛關注。其中匹配場反演[1]是反演淺海聲速剖面的常用方法，然而匹配場技術對環境參數的失配敏感，使得一些學者致力于匹配場反演的環境參數失配問題[2-4]。而后張忠兵等[5]利用波束匹配的方法與常規匹配場反演進行比較，發現波束匹配反演對底質參數失配具有較高的魯棒性。另一類較常用的方法則是利用聲線傳播時間反演海水的聲速剖面[6]。張維等[7-10]提出了基于微擾法的快速聲速剖面反演，在此基礎上分析了基陣傾斜失配的影響，并利用垂直陣不同陣元接收信號到達時間實現了三維聲速剖面反演。由于微擾法可以實現實時的聲速剖面反演，因此也被用于海流的反演中[11-20]。

當利用聲波傳播時間反演聲速剖面時，由于海上實驗過程中信號傳播時間的測量誤差是難免的，并且小的測量誤差有時會給聲速剖面的反演精度帶來極大影響。為了降低反演算法對傳播時間測量誤差的敏感性，本文在微擾法反演聲速剖面的基礎上，通過調整平均聲速剖面以增大聲速擾動量，以此增大平均聲速剖面和實際聲速剖面下的聲線傳播時間差，降低傳播時間測量誤差的影響，提高反演算法對聲速擾動的敏感性，進而提高聲速剖面反演算法的精度。文中對改進微擾近似所帶來的反演聲速剖面偏移進行修正，有效降低了平均聲速剖面調整引入的誤差，進一步提高了反演結果的精度。

1 微擾法改進方法

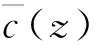
(1)

此時聲速剖面反演轉變為經驗正交函數系數αk的求解。微擾法計算聲線的傳播時間如下

(2)

式中：l表示聲線軌跡。當聲速擾動量足夠小時，l可用平均聲速下的聲線軌跡l0代替。此即為微擾近似的條件：

(3)

考慮n個陣元的水平陣，聲波到達各陣元的傳播時間用ti(i=1,2,…,n)表示，則平均聲速剖面下的聲線傳播時間表示為

(4)

寫成矩陣形式：

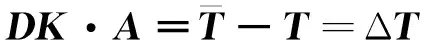
(5)

上述由n個方程組成的線性方程組含有k個未知數。當n>k時，方程組則為超定方程組，用偽逆法求解可得

A=(DKTDK)-1DKTΔT

(6)

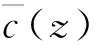
為此，本文考慮通過改變實際聲速剖面的表示形式，即調整平均聲速剖面來改變平均聲速與實際聲速之差，以增大Δt，從而提高Δt的抗干擾能力，最終提高反演算法的魯棒性。

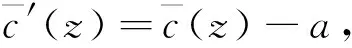
(7)

式中：ci(z)表示聲速剖面數據集中第i條聲速剖面。

(8)

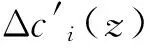
(9)

將此矩陣R′進行特征值分解，則可以用N個正交向量表示R′，有

R′F′=A′F′

(10)

(11)

(12)

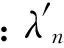
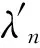
(13)

微擾近似的條件為

(14)

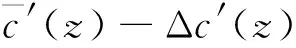
為使反演結果更精確，考慮修正微擾近似引起的誤差，可知Δc′(z)為常數a附近的擾動量。設x(z)為反演結果的偏移量，令反演得到的Δc′(z)為在a+x(z)附近的擾動量，即Δc′(z)≈a+x(z)，代入微擾近似的等式：

(15)

可以得到偏移量滿足的等式：

(16)

解得偏移量：

(17)

2 改進微擾法的仿真驗證

為了驗證本文所提出方法的可行性，做如下的數值計算。數值算例中，假設海底水平，水深50 m，聲信號頻率10 kHz，聲源深度10 m，利用水平陣不同陣元接收信號的傳播時間反演海水中的聲速剖面。水平接收陣深度40 m，水平陣I的陣元距離聲源的水平距離分別為13、13.4、13.8、14.2、14.6、15 km；(水平陣II的陣元距離聲源的水平距離分別為53、53.4、53.8、54.2、54.6、55 km；水平陣III的陣元距離聲源的水平距離分別為13、14、15、16、17、18 km)，按從近到遠的順序用1～6號對陣元命名，仿真環境的示意圖見圖1。

圖1 仿真環境示意圖Fig.1 The diagram of the environment

仿真計算中，將真實的平均聲速剖面下調20 m/s得到調整后的平均聲速剖面，分別使用調整前后的平均聲速剖面和對應的經驗正交函數進行反演計算，表1給出了平均聲速剖面調整前后的平均聲速與實際聲速下的聲線傳播時間差。可以看出，聲速剖面調整后的傳播時間擾動量的量級為10-1s，遠大于聲速剖面調整前10-3s，此時傳播時間擾動抗傳播時間測量誤差干擾的能力得到增強，反演結果的精度得到提高。值得注意的是本文提出的方法相對于傳統的微擾法僅僅是在最初的平均聲速剖面表示上給定一水平偏移量，以此來改變經驗正交函數表示。因此相對于傳統的微擾法沒有加大計算量，沒有犧牲計算時間。

考慮傳播時間測量誤差對反演算法的影響，假設測時誤差服從高斯分布，均值為零，方差為10-4s。進行100次聲速剖面反演，取反演聲速的平均值作為最終反演結果。圖2給出了平均聲速剖面調整前后，利用水平陣1各陣元接收信號的傳播時間進行反演獲得的聲速剖面。比較圖2(a)、(b)中5條樣本聲速的反演結果可以看出，平均聲速調整后，反演獲得的每條聲速剖面均與待反演聲速剖面更接近，證明了改進聲速剖面反演算法的可行性。然而從圖2(a)、(b)的反演誤差曲線可以看出，圖2(b)中的反演結果存在0.3 m/s的水平偏移，這驗證了上節中的理論分析。應用式(17)對該結果進行補償，圖2(c)給出了補償后的聲速剖面。可以發現，圖2(c)的反演結果(實線)與實際待反演的聲速剖面(虛線)幾乎完全重合。從表2給出的反演誤差可以看出，本文提出的反演算法相比于傳統的微擾法有更高的反演精度，驗證了此方法的可行性。

表1 平均聲速剖面與實際聲速剖面下的傳播時間差

Table 1 Time difference between average sound speed profile and real sound speed profile

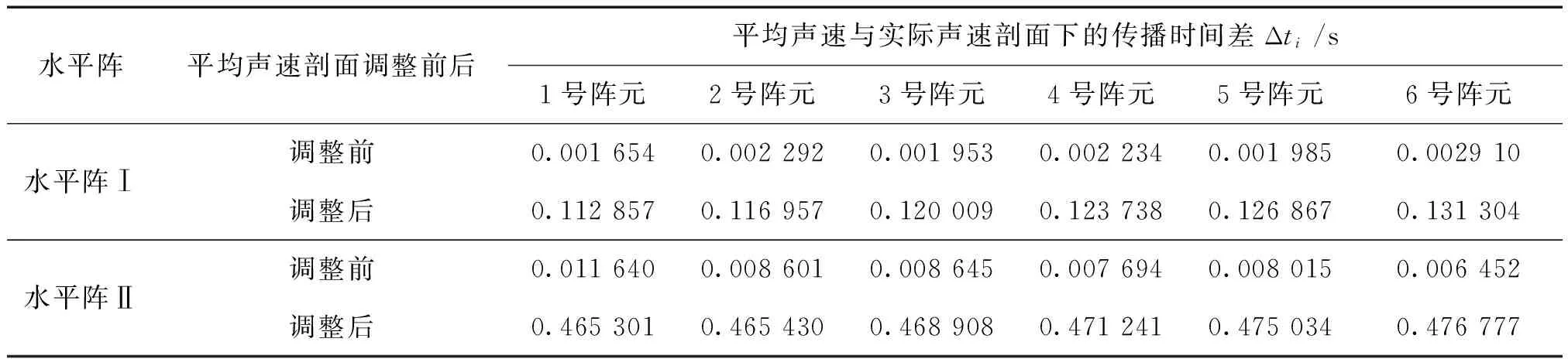
水平陣平均聲速剖面調整前后平均聲速與實際聲速剖面下的傳播時間差Δti/s1號陣元2號陣元3號陣元4號陣元5號陣元6號陣元水平陣Ⅰ調整前0.0016540.0022920.0019530.0022340.0019850.002910調整后0.1128570.1169570.1200090.1237380.1268670.131304水平陣Ⅱ調整前0.0116400.0086010.0086450.0076940.0080150.006452調整后0.4653010.4654300.4689080.4712410.4750340.476777

表2 水平陣I反演結果

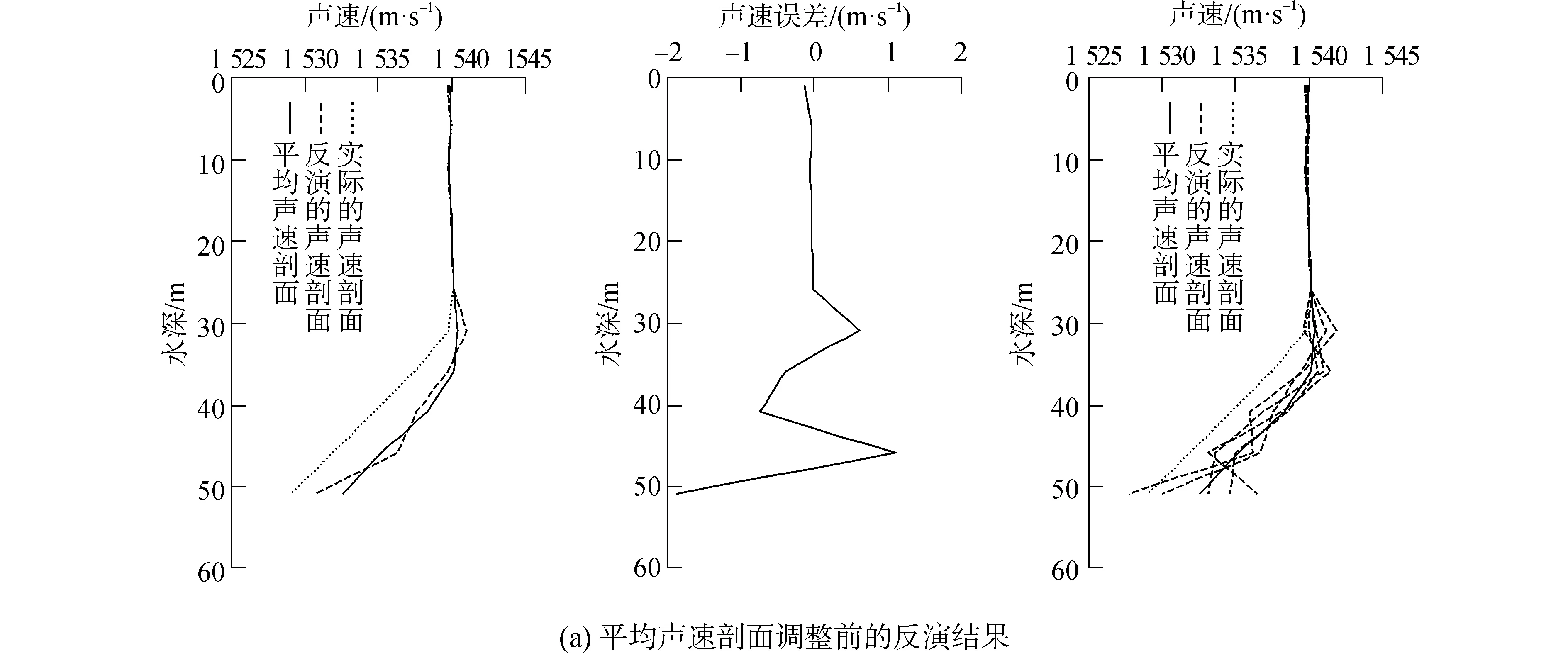
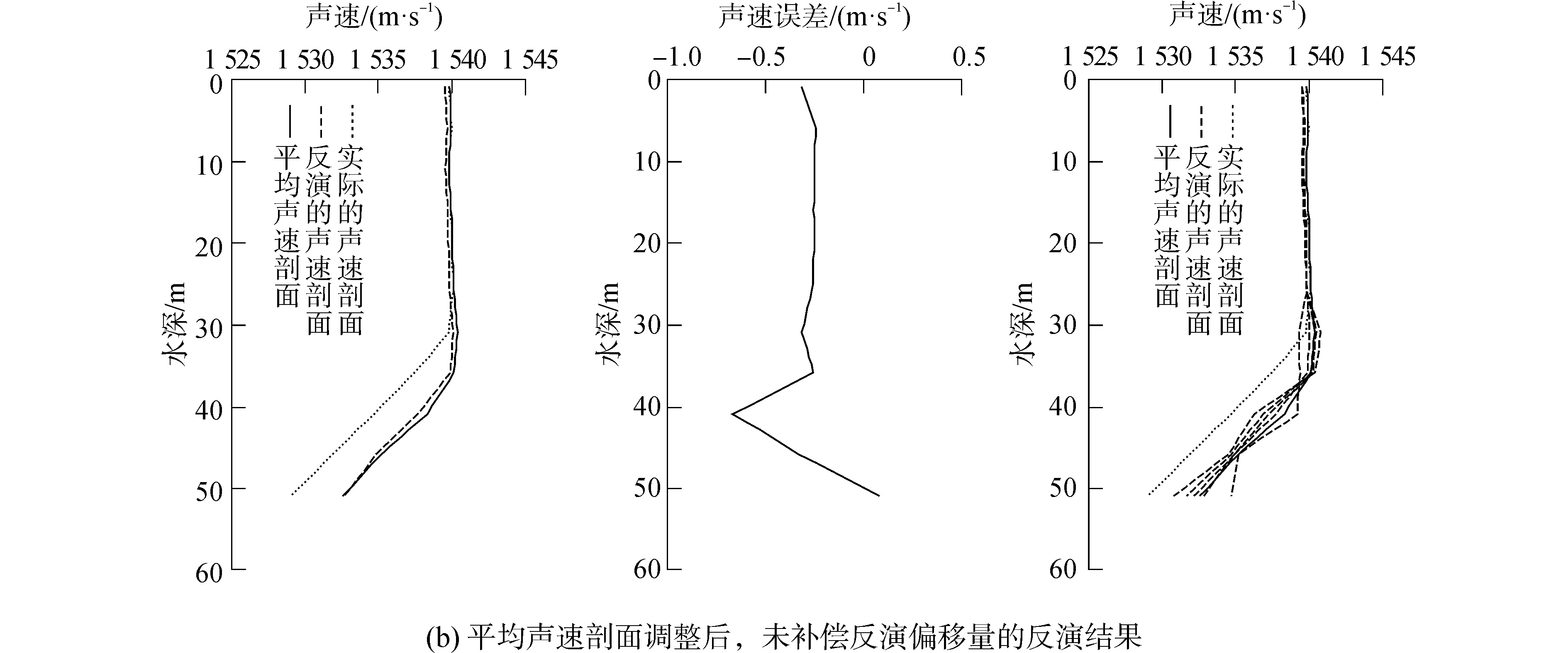
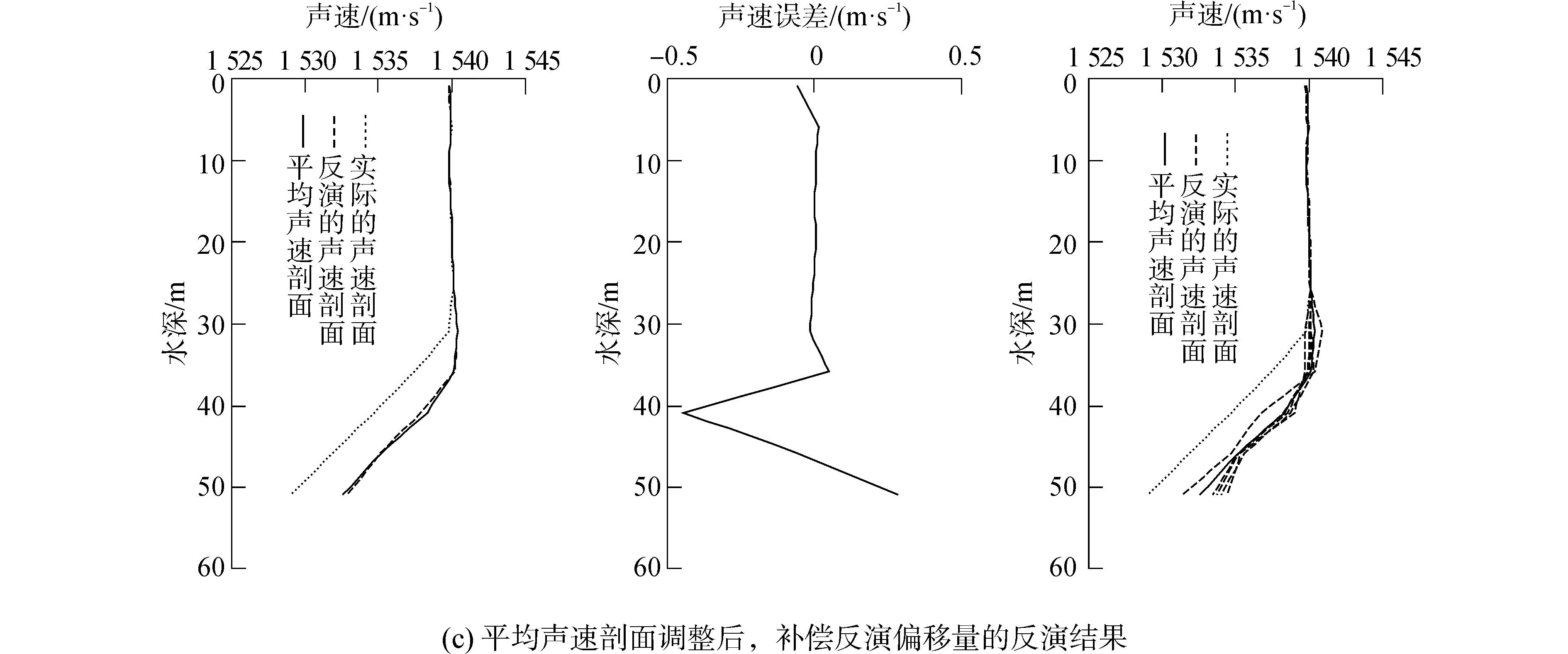
圖2 水平陣I反演結果Fig.2 The results of inversion by horizontal array I

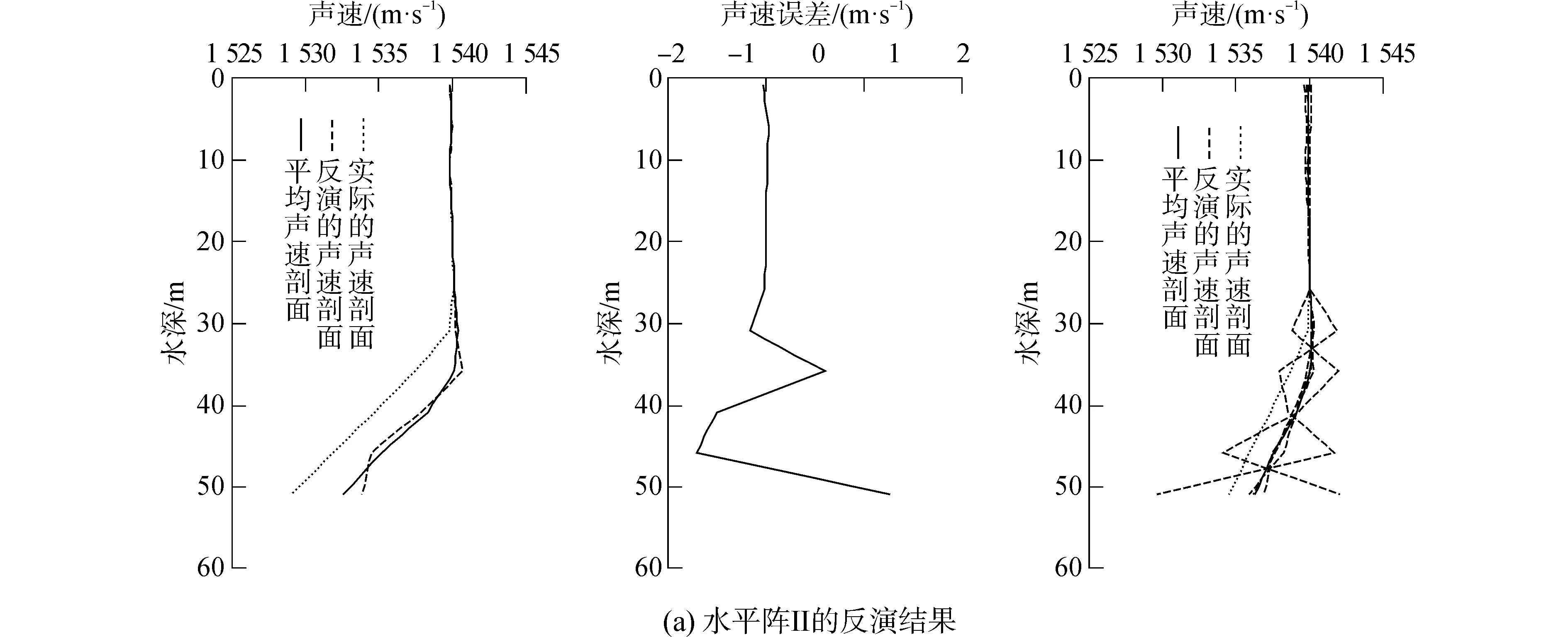
圖3 傳統微擾法的反演結果Fig.3 The results of inversion by traditional perturbation method

為了驗證本文提出方法的有效性，下文利用水平陣Ⅱ和水平陣Ⅲ，采用傳統微擾法進行仿真研究，反演結果見圖3。且水平陣Ⅱ反演聲速剖面的最大誤差為1.173 m/s，均方根誤差為0.324 m/s；水平陣Ⅲ反演聲速剖面的最大誤差為0.578 m/s，均方根誤差為0.298 m/s。水平陣Ⅱ相對于水平陣Ⅰ而言，陣元間距相同，但距離聲源的水平距離更遠。與表2數據比較發現，當陣元間距一定的情況下，增大基陣距離聲源的水平距離可以提高反演結果的精度，這是因為聲速擾動量敏感性增大的結果。水平陣Ⅲ相對于水平陣Ⅰ有著更大的陣元間距，比較發現，增大陣元間距亦可以提高反演結果的精度，這是因為聲波到達各陣元的時間差得到增大，聲線軌跡近似導致聲線傳播時間誤差的影響得到降低。

雖然通過增大基陣與源的水平距離或擴大水平陣陣元間距可以降低反演結果的誤差，但是傳統微擾法的反演精度仍比本文提出的改進算法低。從圖3還可看出，利用水平陣Ⅱ和水平陣Ⅲ反演獲得的聲速剖面與實際聲速剖面相差較大，而本文提出的方法的反演結果如圖2(c)所示，任意一條反演得到的聲速剖面都與實際聲速剖面極為吻合，驗證了本文提出方法的反演性能。

3 結論

本文在傳統微擾法反演聲速剖面的基礎上，通過調整平均聲速剖面以增大聲速擾動量，增大了聲速擾動引起傳播時間的擾動量，提出了聲速剖面反演改進算法，數值仿真得到以下結論：

1)聲速剖面調整不僅提高了反演算法抗傳播時間測量誤差的能力，同時也增強了算法對聲速擾動的敏感性，有效提高了反演結果的精度。

2)通過對聲速剖面調整引入的聲速偏移進行修正，進一步降低了改進算法的反演誤差，進一步提高了反演結果的精度。

3)本文提出的方法相比于傳統的微擾法在保證計算時間的情況下提高了反演結果的精度，降低了聲波傳播時間測量誤差對聲速剖面反演算法的影響，驗證了本文提出方法的可行性。

此外本文提出的改進算法可應用于利用經驗正交函數進行反演聲速剖面或海洋流速中，降低測時誤差的影響。本文僅對此算法進行了仿真分析，海上實驗的驗證將是我們下一步研究的重點內容。

[1]楊坤德. 水聲信號的匹配場處理技術研究[D]. 西安: 西北工業大學, 2003. YANG Kunde. A study on matched field processing of underwater acoustic signals[D]. Xi’an: Northwestern Polytechnical University, 2003.

[2]SHANG E C, WANG Y Y. Environmental mismatching effects on source localization processing in mode space[J]. The journal of the acoustical society of America, 1991, 89(5): 2285-2290.

[3]黃益旺. 淺海遠距離匹配場聲源定位研究[D]. 哈爾濱: 哈爾濱工程大學, 2005. HUANG Yiwang. Research on long-range source localization by matched field processing in shallow water[D]. Harbin: Harbin Engineering University, 2005.

[4]趙航芳, 李建龍, 宮先儀. 不確實海洋中最小方差匹配場波束形成對環境參量失配的靈敏性分析[J]. 哈爾濱工程大學學報, 2011, 32(2): 200-208. ZHAO Hangfang, LI Jianlong, GONG Xianyi. Sensitivity of minimum variance matched-field beamforming to an environmental parameter mismatch in an uncertain ocean channel[J]. Journal of Harbin engineering university, 2011, 32(2): 200-208.

[5]張忠兵, 馬遠良, 楊坤德, 等. 淺海聲速剖面的匹配波束反演方法[J]. 聲學學報, 2005, 30(2): 103-107. ZHANG Zhongbing, MA Yuanliang, YANG Kunde, et al. Inversion for sound speed profile in shallow water using matched-beam processing[J]. Acta acustica, 2005, 30(2): 103-107.

[6]唐俊峰, 楊士莪. 由傳播時間反演海水中的聲速剖面[J]. 哈爾濱工程大學學報, 2006, 27(5): 733-736, 756. TANG Junfeng, YANG Shi’e. Sound speed profile in ocean inverted by using travel time[J]. Journal of Harbin Engineering University, 2006, 27(5): 733-736, 756.

[7]張維, 楊士莪, 黃益旺, 等. 基于爆炸聲傳播時間的聲速剖面反演[J]. 振動與沖擊, 2012, 31(23): 6-11. ZHANG Wei, YANG Shi’e, HUANG Yiwang, et al. Inversion of sound speed profile based on explosive sound transmission time[J]. Journal of vibration and shock, 2012, 31(23): 6-11.

[8]張維. 三維淺海環境下全海深聲速剖面快速反演研究[D]. 哈爾濱: 哈爾濱工程大學, 2013. ZHANG Wei. Inversion of sound speed profile in three-dimensional shallow water[D]. Harbin: Harbin Engineering University, 2013.

[9]張維, 楊士莪, 黃益旺, 等. 基于微擾法的快速聲速剖面反演[J]. 上海交通大學學報, 2013, 47(8): 1287-1291. ZHANG Wei, YANG Shi’e, HUANG Yiwang, et al. Fast inversion of sound speed profile based on perturbation method[J]. Journal of Shanghai jiao tong university, 2013, 47(8): 1287-1291.

[10]張維, 楊士莪, 黃勇. 聲速剖面反演對基陣傾斜失配的敏感性研究[J]. 聲學學報, 2015, 40(5): 649-654. ZHANG Wei, YANG Shi’e, HUANG Yong. Research about sensitivity of array inclination on sound speed profile inversion[J]. Acta acustica, 2015, 40(5): 649-654.

[11]邢傳璽. 淺海局部海域聲速剖面和海流分布反演方法研究[D]. 哈爾濱: 哈爾濱工程大學, 2015. XING Chuanxi. The inversion method research of shallow sea local area sound speed profile and current speed distribution[D]. Harbin: Harbin Engineering University, 2015.

[12]邢傳璽, 董國芳. 一種基于聲傳播時間的海流垂直剖面求解方法[J]. 云南民族大學學報: 自然科學版, 2016, 25(5): 441-446. XING Chuanxi, DONG Guofang. A problem-solving method for the vertical profile of the ocean currents based on sound propagation time[J]. Journal of Yunnan minzu university: natural sciences edition, 2016, 25(5): 441-446.

[13]WANGSQ,WULX,WANGHW, et al. Inversion of temperature, acoustic propagation perturbation andinternalwave in 2001 South China Sea experiment[J].Progress in natural science, 2004 14(6): 635-640.

[14]LYNCH J F, RAMP S R, CHIU C S, et al. Research highlights from the Asian Seas International Acoustics Experiment in the South China Sea[J].IEEE journal of oceanic engineering, 2004, 29(4):1067-1074.

[15]TANIGUCHI N, KANEKO A, YUAN Y, et al. Long-term acoustic tomography measurement of ocean currents at the northern part of the Luzon Strait[J]. Geophysical research letters, 2010, 37(7):256-265.

[16]TANIGUCHI N, HUANG C F, KANEKO A, et al. Measuring the Kuroshio Current with ocean acoustic tomography[J]. Journal of the acoustical society of america, 2013, 134(4):3272-3281.

[17]ZHU X H, KANEKO A, WU Q, et al. Mapping tidal current structures in Zhitouyang Bay, China, using coastal acoustic tomography[J]. IEEE journal of oceanic engineering, 2013, 38(2):285-296.

[18]ZHU X H, ZHANG C, WU Q, et al. Measuring discharge in a river with tidal bores by use of the coastal acoustic tomography system[J]. Estuarine coastal & shelf science, 2012, s 104-105(2):54-65.

[19]TANIGUCHI N, HUANG C F, KANEKOA, et al. Measuring the Kuroshio current with ocean acoustic tomography[J]. Journal of the acoustical society of America,2013,134(4):3272-3281.

[20]ZHU X H, WU Q, ZHANG C, et al. A coastal acoustic tomography experiment in the Sanmen Bay, China[C]. International Congress On Image and Signal Processing. IEEE, 2010:3820-3824.

Improved perturbation method for sound speed profile inversion

ZHENG Guangying1,2, HUANG Yiwang1,2

(1.Acoustic Science and Technology Laboratory, Harbin Engineering University, Harbin 150001, China; 2.College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China)

To minimize the impact of travel-time measurement errors on acoustic inversion, an improved algorithm for sound speed profile inversion was presented in this paper. By adjusting the mean sound speed profile, the algorithm can increase the disturbance of sound speed, which can further increase the disturbance of ray travel-time caused by the disturbance of sound speed, thereby lowering the effect of the time measurement error on the inversion algorithm and increasing the sensitivity of the new algorithm to the perturbation of sound velocity. Numerical calculation cases show that the maximum error of sound speed profile inversion by the traditional perturbation method under the same conditions is 1.478 m/s, while the maximum error of the improved algorithm can be lowered to 0.403 m/s. The result shows that the improved algorithm can effectively lower the effect of the measurement error of travel time on the inversion result of the sound velocity profile and the inversion precision is higher than the perturbation method.

sound speed profile; perturbation method; inversion; empirical orthogonal function(EOF); traveltime of sound ray; time measurement error

2016-03-23.

日期：2017-01-11.

國家自然科學基金項目(11274078).

鄭廣贏(1992-)，男，博士研究生； 黃益旺(1975-)，男，教授，博士.

黃益旺，E-mail: huangyiwang@hrbeu.edu.cn.

10.11990/jheu.201603075

P733.2

A

1006-7043(2017)03-0371-07

鄭廣贏, 黃益旺.微擾法聲速剖面反演改進算法[J]. 哈爾濱工程大學學報, 2017, 38(3):371-377.

ZHENG Guangying, HUANG Yiwang.Improved perturbation method for sound speed profile inversion[J]. Journal of Harbin Engineering University, 2017, 38(3):371-377.

網絡出版地址：http://www.cnki.net/kcms/detail/23.1390.u.20170111.1509.036.html