差分方程應(yīng)用于市場經(jīng)濟(jì)中蛛網(wǎng)模型
陳明+張愛國+彭慧丹
摘 要:針對(duì)市場經(jīng)濟(jì)中需求與供應(yīng)關(guān)系而導(dǎo)致的價(jià)格與數(shù)量的振蕩現(xiàn)象,首先用圖形方法建立蛛網(wǎng)模型,并從圖像角度分析振蕩穩(wěn)定條件。為從理論上得到穩(wěn)定條件,引入差分方程并加以改進(jìn)而建立數(shù)學(xué)模型,從而得到穩(wěn)定條件。接著對(duì)模型進(jìn)行分析,最后簡單介紹經(jīng)濟(jì)不穩(wěn)定時(shí)的干預(yù)措施。
關(guān)鍵詞:差分方程;蛛網(wǎng)模型;平衡點(diǎn);穩(wěn)定;市場經(jīng)濟(jì)
中圖分類號(hào):F224 文獻(xiàn)標(biāo)志碼:A 文章編號(hào):1673-291X(2017)07-0005-02
市場經(jīng)濟(jì)中當(dāng)期商品價(jià)格是由消費(fèi)者的需求量而定,而下期商品數(shù)量是由生產(chǎn)者的供應(yīng)量而定。需求關(guān)系與供應(yīng)關(guān)系導(dǎo)致商品價(jià)格與數(shù)量必定產(chǎn)生振蕩現(xiàn)象。若振幅逐漸變小至平穩(wěn),則經(jīng)濟(jì)穩(wěn)定;反之若振幅逐漸變大至不可控制,則經(jīng)濟(jì)紊亂。
一、蛛網(wǎng)模型
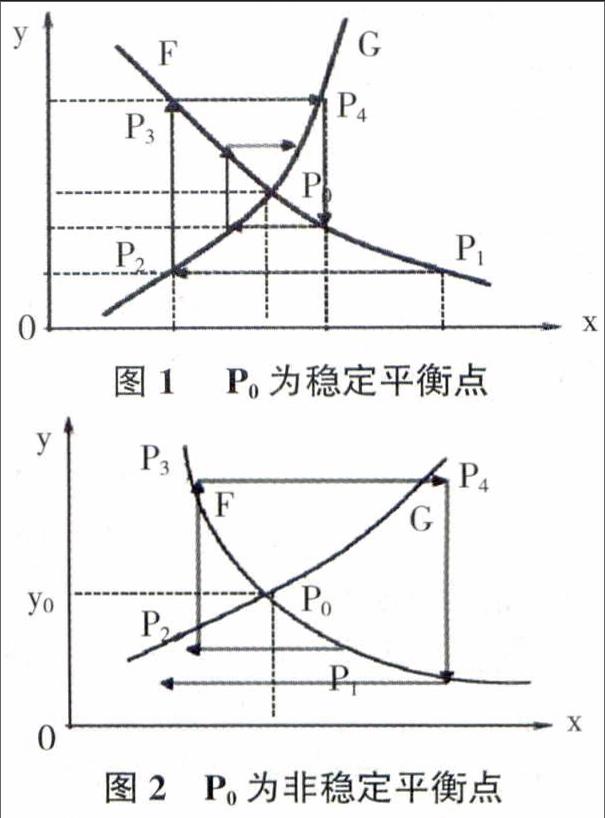
設(shè)第i個(gè)周期商品數(shù)量為xi,價(jià)格為yi,i=1,2,3…。這個(gè)周期是指商品的1個(gè)生產(chǎn)周期,例如對(duì)蘋果而言,其指的是種植周期。由于商品價(jià)格主要取決于商品數(shù)量,令yi=F(xi)為商品需求函數(shù),圖1中所示下降曲線為需求曲線。由于下個(gè)周期的商品數(shù)量xi+1取決于上個(gè)周期價(jià)格yi,令xi+1=H(yi)或yi=G(xi+1)為供應(yīng)函數(shù),這里G為H的反函數(shù)。圖2中所示上升曲線為供應(yīng)曲線。在圖1中,需求曲線與供應(yīng)曲線交于P0(x0,y0)點(diǎn),稱該點(diǎn)為平衡點(diǎn),即數(shù)量與價(jià)格一直維持在該點(diǎn)不變。但實(shí)際并非如此,當(dāng)商品數(shù)量變化到x1后,價(jià)格y1由函數(shù)F決定,繼而產(chǎn)生點(diǎn)p1(x1,y1),以此類推,會(huì)產(chǎn)生系列點(diǎn)p2(x2,y2),p3(x3,y3),…。若按圖1所示方向趨近P0,表明P0為穩(wěn)定平衡點(diǎn),即市場經(jīng)濟(jì)穩(wěn)定。若其按圖2所示方向遠(yuǎn)離P0,表明P0為不穩(wěn)定平衡點(diǎn),商品數(shù)量與價(jià)格振蕩越來越大,即市場經(jīng)濟(jì)不穩(wěn)定。圖1與圖2產(chǎn)生的形如蛛網(wǎng)的折線稱為蛛網(wǎng)模型。觀察圖1和圖2可知,在P0點(diǎn)當(dāng)函數(shù)G斜率大于函數(shù)F斜率時(shí),P0是穩(wěn)定平衡點(diǎn),反之即為非穩(wěn)定平衡點(diǎn)。但是,這僅僅限于圖像上觀察,為了從理論上說明平衡點(diǎn)穩(wěn)定條件,下面將差分方程應(yīng)用到蛛網(wǎng)模型當(dāng)中。
二、差分方程模型
在引入差分方程之前,先將供應(yīng)函數(shù)做下改進(jìn),將決定商品數(shù)量xi+1前一周期的價(jià)格yi改為前兩個(gè)周期yi和yi-1,這樣可以體現(xiàn)生產(chǎn)者管理水平的提高,這里不妨取yi和yi-1平均值,即有Xi+1=H(yi/2+yi-1/2)。在P0附近用直線來近似曲線F和H,可將需求函數(shù)與供應(yīng)函數(shù)近似為:
其特征根為λ1,2=(-mn±)/4。當(dāng)mn>8時(shí),方程有特征根位于單位圓外,所以此時(shí)P0點(diǎn)不穩(wěn)定。當(dāng)mn<8時(shí),則有|λ1,2|=,為使得特征根位于單位圓內(nèi),必有mn<2,此時(shí)P0點(diǎn)穩(wěn)定。綜上可知,P0點(diǎn)穩(wěn)定的條件為mn<2。相比前面直接從圖形上觀察,利用差分方程模型可以得到數(shù)值上的結(jié)論。
三、模型分析
首先,m的大小反映了消費(fèi)者對(duì)商品需求的敏感程度,假如其為生活必需品,稍有不足,消費(fèi)者必?fù)屬彛瑒tm值偏大。假如為非必需品,若稍有不足,消費(fèi)者心態(tài)平和并無較強(qiáng)購買欲,則m值偏小。n的大小反映了生產(chǎn)者對(duì)商品價(jià)格的敏感程度,假如生產(chǎn)者追求短期利益,價(jià)格略增即加大生產(chǎn),則n值較大;反之假如其有生產(chǎn)規(guī)劃,則n值較小。其次,當(dāng)n固定,m越小,需求曲線越平滑,即消費(fèi)者對(duì)商品需求不高,穩(wěn)定條件越容易滿足,則經(jīng)濟(jì)形式越穩(wěn)固。當(dāng)m固定,n越小,生產(chǎn)曲線越平滑,即生產(chǎn)者對(duì)商品價(jià)格不敏感,穩(wěn)定條件也越容易滿足,則經(jīng)濟(jì)形式越穩(wěn)固。但當(dāng)m、n都較大時(shí),即生產(chǎn)者與消費(fèi)者分別對(duì)價(jià)格與需求都很敏感,則穩(wěn)定條件不易滿足,經(jīng)濟(jì)不穩(wěn)定。
四、經(jīng)濟(jì)不穩(wěn)定時(shí)的干預(yù)措施
方法一,m值盡量小,不妨令m=0,則mn=0<2恒成立,這種方法實(shí)際上相當(dāng)于抑制物價(jià),無論商品多少,不予改變。
方法二,n值盡量小,不妨令n=0,則mn=0<2恒成立,這種方法實(shí)際上相當(dāng)于保持市場商品供應(yīng)平穩(wěn),商品過多,予以回購;商品短缺,予以調(diào)撥。
參考文獻(xiàn):
[1] 趙靜,但琦.數(shù)學(xué)建模與數(shù)學(xué)實(shí)驗(yàn)[M].北京:高等教育出版社,2014.
[2] 埃萊迪.差分方程導(dǎo)論[M].北京:世界圖書出版社,2013.
[3] 劉喜梅.經(jīng)濟(jì)數(shù)學(xué)[M].北京:中國鐵道出版社,2008.
[4] 錢和平,徐清舟.數(shù)學(xué)建模融入經(jīng)濟(jì)數(shù)學(xué)中案例及分析大學(xué)數(shù)學(xué)[J].大學(xué)數(shù)學(xué),2012,(3):92-96.
[責(zé)任編輯 吳高君]

