室內爆炸與火災聯合作用下約束鋼柱損傷評估

丁 陽，陳 曄，師燕超

(1.天津大學 建筑工程學院，天津 300072；2.天津大學 濱海土木工程結構與安全教育部重點實驗室，天津 300072)

室內爆炸與火災聯合作用下約束鋼柱損傷評估

丁 陽1,2，陳 曄1，師燕超1,2

(1.天津大學 建筑工程學院，天津 300072；2.天津大學 濱海土木工程結構與安全教育部重點實驗室，天津 300072)

結構體系提供的約束剛度和附加質量會顯著影響鋼柱在爆炸下的動力響應，同時火災下結構對熱膨脹的約束會導致鋼柱內產生附加軸力，受力特性與無約束柱明顯不同。采用引入損傷的Johnson-Cock強度模型分析了約束鋼柱在室內爆炸荷載作用下的損傷情況，建立了評估約束鋼柱在爆炸與火災聯合作用下破壞情況的壓力-沖量-時間曲面圖及表達式。為了說明結構約束的影響，將計算結果與無約束鋼柱在爆炸與火災聯合作用下的破壞時間進行對比，并進一步分析了超壓時程曲線形狀、約束剛度及鋼柱幾何尺寸對P-I-t曲面圖的影響。結果表明，當爆炸荷載強度較小時，約束鋼柱的破壞時間早于無約束鋼柱，當爆炸荷載強度較大時，約束鋼柱的破壞時間晚于無約束鋼柱；超壓時程曲線形狀參數越大，約束鋼柱在爆炸作用下越易破壞；約束剛度對鋼柱在爆炸與火災聯合作用下的破壞時間基本無影響；當爆炸損傷較小時，鋼柱壁厚對破壞時間影響很小，當爆炸損傷較大時，鋼柱壁厚度越大，鋼柱越易破壞，但在壓力-沖量-時間空間中，仍為壁厚越小、柱高越高的鋼柱越易破壞。

爆炸；火災；約束鋼柱；損傷評估；參數分析

鋼結構具有自重輕，強度高，韌性好，施工進度快等特點，被廣泛應用于大跨空間結構、工業廠房、高層建筑結構中。鋼柱作為結構主要受力構件，其破壞往往會導致結構發生局部破壞甚至連續倒塌，因此對鋼柱力學性能的研究具有實際工程意義。建筑物內發生爆炸后，會引發火災等次生災害。鋼材的耐火性差，爆炸與火災的聯合作用會對鋼柱乃至整體結構造成嚴重破壞，因此對鋼柱在爆炸與火災聯合作用下的響應進行研究已成為工程領域的研究熱點。

LIEW等[1-3]采用不同的單元類型將爆炸與火災聯合作用下鋼柱的響應進行分析，并擴展到三維鋼框架分析。閻石等[4]用數值分析了輕鋼柱在高溫與爆炸作用下的動力響應及破壞模式。方秦等[5]提出了一種爆炸與火災聯合作用下結構破壞的全過程數值模擬方法，并評估了鋼柱在聯合作用下的破壞效應。DING等[6]采用引入損傷因子的Johnson-Cock強度模型，評估了方鋼柱在爆炸和火災聯合作用下的損傷情況，并提出了P-I-t曲面計算式。然而，上述分析均假定鋼柱上端可沿豎向自由移動，未按實際情況考慮柱端約束及附加質量的影響。

鋼柱處于結構體系中，結構提供的約束對鋼柱行為響應有一定程度的影響。在爆炸作用下，柱端約束剛度和質量會顯著影響鋼柱動力響應，在火災下約束鋼柱因熱膨脹受限而承受附加軸力，性能與無約束鋼柱明顯不同[7-8]，忽略柱端約束及質量的影響會導致計算結果不符合實際。此外，目前對鋼柱在室內爆炸與火災聯合作用下的損傷研究尚少。因此，本文采用考慮損傷的Johnson-Cock強度模型分析了約束鋼柱在室內爆炸作用下的損傷情況，然后，根據約束鋼柱破壞溫度的定義，得到了評估約束鋼柱在爆炸與火災聯合作用下破壞情況的壓力-沖量-時間(P-I-t)曲面圖及表達式。為了說明考慮結構約束的必要性，對比了約束鋼柱與無約束鋼柱在爆炸與火災聯合作用下的破壞時間，并定量分析了超壓時程曲線形狀、約束剛度和鋼柱幾何尺寸對P-I-t曲面圖的影響。

1 爆炸與火災聯合作用下約束鋼柱損傷分析模型

1.1 約束剛度計算

爆炸荷載作用下，結構體系提供的約束剛度、附加質量和轉動慣量會顯著影響鋼柱的動力響應，且約束剛度與靜態、準靜態荷載作用下的剛度明顯不同。火荷載作用下，約束的存在限制鋼柱的膨脹變形，鋼柱因承受附加軸力而更易破壞。因此，正確計算結構提供的約束剛度是分析鋼柱在爆炸與火災聯合作用下真實響應的關鍵。

爆炸荷載作用下，結構構件的動力響應具有一定的局部性，只與構件及其周圍相連的構件有關，因此，將整個框架體系簡化為圖1所示的分析模型來計算鋼柱在爆炸作用下的柱端約束剛度[9]。根據結構動力學相關知識計算單根構件提供的約束剛度、集中質量和轉動慣量[10]，列于表1，進而組合得到爆炸荷載作用下豎向約束的等效剛度Keq和集中質量Meq為

Keq=2Kb+Kc

(1)

Meq=2Mb+Mc

(2)

(3)

(4)

火荷載作用下，柱端約束剛度采用ANSYS有限元軟件數值算得。

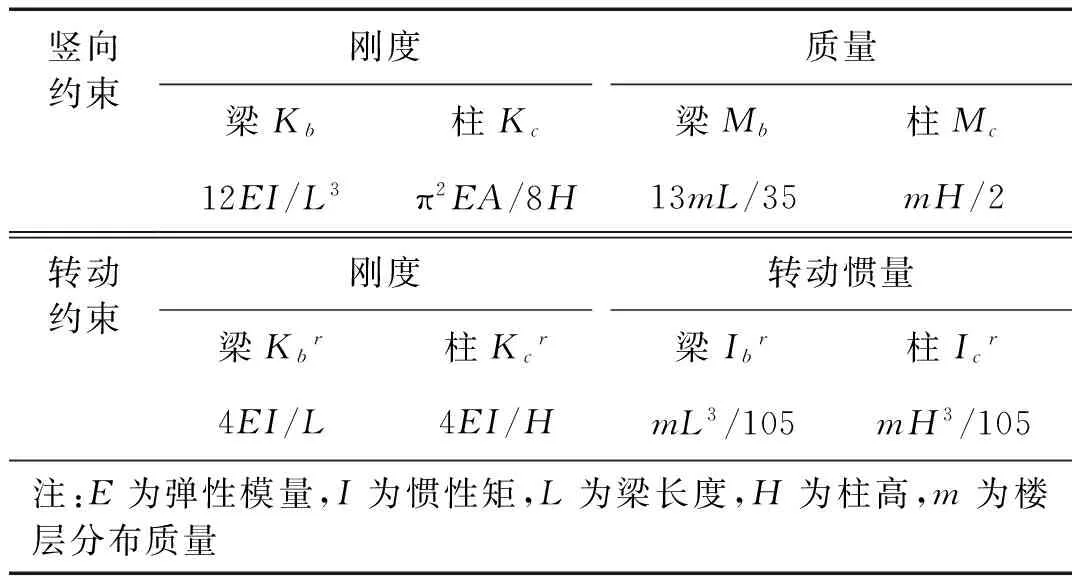
表1 單根構件提供約束的計算式Tab.1 Formula for calculating restraint provided by single member

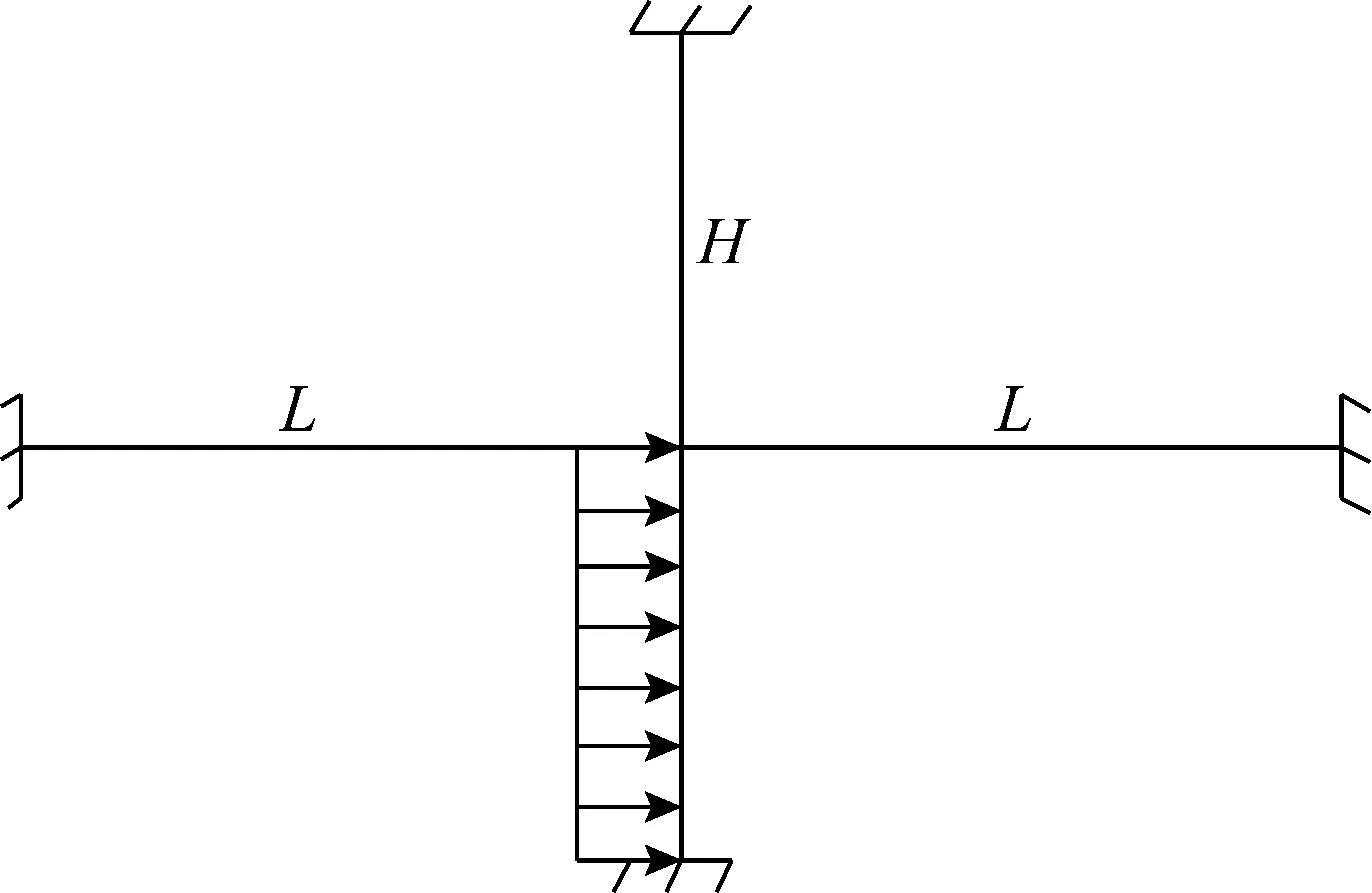
圖1 框架簡化分析模型Fig.1 The simplified model of frame

1.2 爆炸荷載與火荷載

建筑屋室內部往往存在大量可燃物，一旦發生爆炸，有很高的概率誘發次生火災，因此選擇室內爆炸工況。由于四周墻壁、樓板和地面的反射，室內爆炸超壓的分布及時程曲線復雜。參考美國UFC規范[11]，將室內爆炸超壓時程曲線簡化為雙線性形式，如圖2所示，分別代表爆炸沖擊波作用階段和爆炸產物作用階段，并假設約束鋼柱上的爆炸荷載均勻分布。定義參數ρ和τ，表達式分別為式(5)和式(6)。由圖2可知，參數ρ和τ決定了室內爆炸超壓時程曲線的形狀，通過改變參數ρ和τ的取值，便可得到不同形狀的室內爆炸超壓時程曲線，但需滿足ρ+τ≤1 。設定最大峰值超壓、氣體壓力持續時間及上述2個參數的值便能確定作用在鋼柱上的爆炸荷載。

(5)

(6)

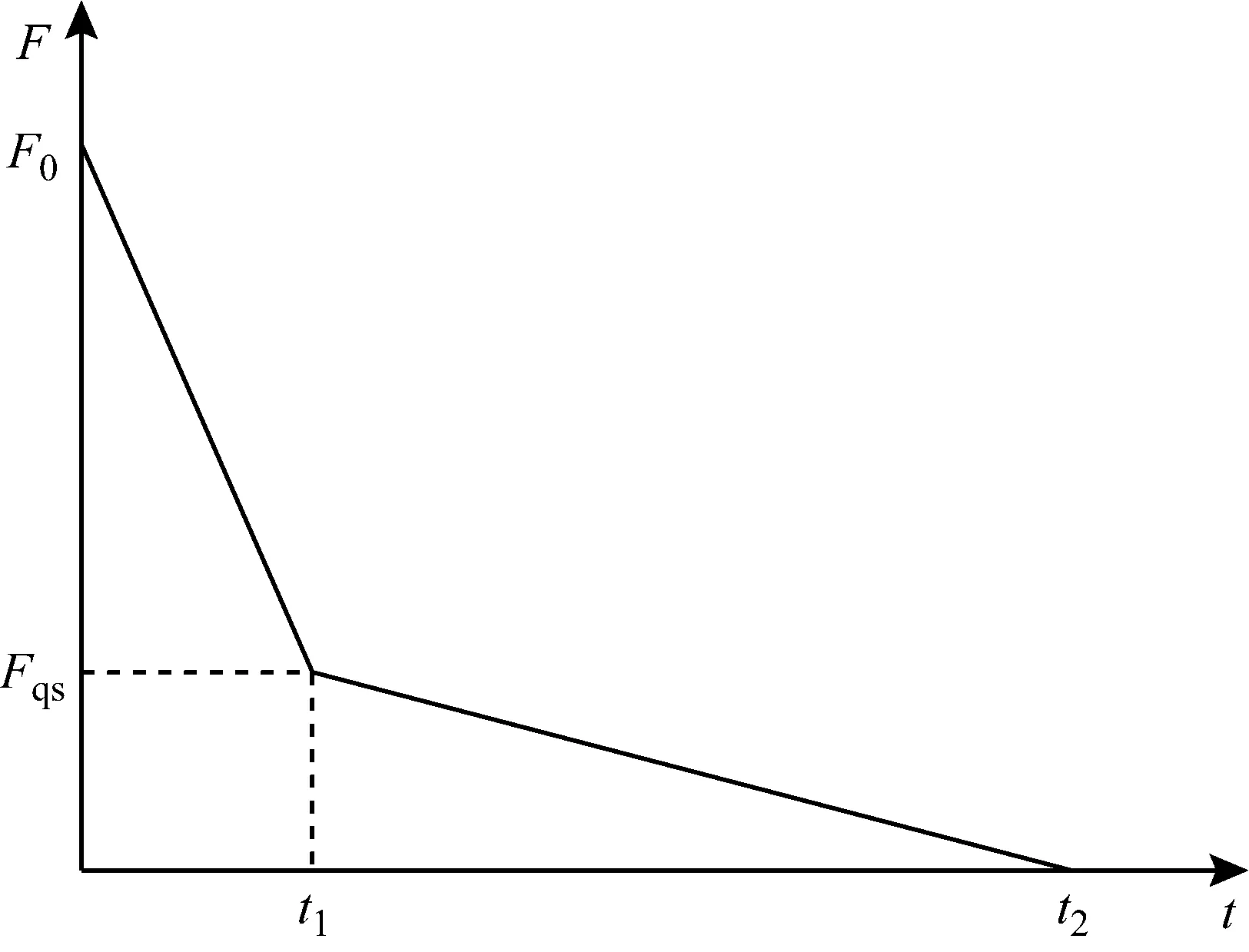
圖2 室內爆炸超壓時程曲線簡化模型Fig.2 Simplified model of confined explosion

爆炸誘發火災場的溫度分布與可燃物質量、位置、屋室通風條件等影響因素有關，具有很強的隨機性。為方便抗火研究，本文采用國際上普遍認可的ISO834標準升溫曲線[12]來表征爆炸誘發火災場的升溫。

2 爆炸荷載作用下約束鋼柱損傷評估

2.1 鋼柱數值模型

選擇某鋼框架底層中心的鋼柱為研究對象。鋼框架跨度為6 m，層高為3.6 m，鋼柱采用方鋼管，截面尺寸為300×300×16×16(mm2)，鋼梁采用H型鋼，截面尺寸為H350×200×12×16(mm2)。框架柱簡化幾何模型如圖3(a)所示，柱底固結，柱頂約束平動，并施加豎向和轉動彈簧模擬框架對鋼柱的約束。采用LS-DYNA提供的shell單元建立約束鋼柱有限元模型，考慮1/1 000柱高的初彎曲。在鋼柱兩端建立剛性塊以避免應力集中，在柱頂施加0.2Fp(Fp為鋼柱極限承載力)的豎向荷載，表示上部結構傳遞的荷載。通過對不同網格尺寸計算結果和效率的對比，選擇網格尺寸為15 mm，約束鋼柱的有限元模型如圖3(b)所示。爆炸荷載作用下鋼材的本構模型采用汪明提出的引入損傷因子的Johnson-Cock強度模型[6]，高溫下鋼材本構模型采用EC3模型[13]。

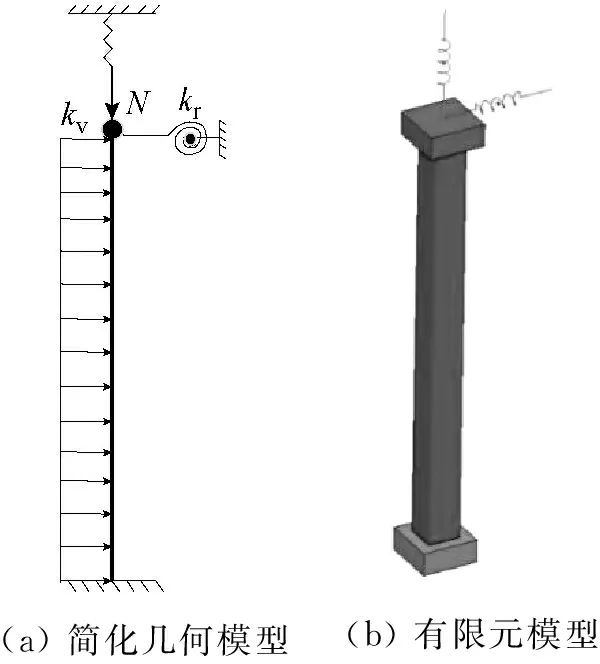
(a)簡化幾何模型(b)有限元模型

圖3 約束鋼柱簡化及有限元模型

Fig.3 The model of restrained steel column

2.2 約束鋼柱損傷評估

鋼柱作為豎向承力構件，其損傷程度與豎向承載力的退化程度有關。因此，以剩余承載力作為損傷判定準則[14]，定義損傷指數為

(7)

式中：Rresi為爆炸荷載作用后鋼柱的剩余豎向承載力；Rini為鋼柱初始豎向承載力。

根據不同的損傷指數，將約束鋼柱的損傷程度劃分為4個等級[12]，如表2所示。

表2 損傷程度劃分Tab.2 Categorization of damage level

壓力-沖量(P-I)曲線圖目前普遍應用于爆炸荷載作用下防護結構的損傷評估中。P-I曲線分為三段，分別對應沖量爆炸荷載、動力爆炸荷載和準靜態爆炸荷載。每一條P-I曲線對應一個損傷值，壓力-沖量空間被多條P-I曲線按損傷等級分割。

本文利用數值分析方法，得到了約束鋼柱在不同爆炸荷載作用后的剩余承載力。根據損傷指數的定義，將產生相同損傷指數的爆炸荷載標記在壓力-沖量空間中，得到了用于評估約束鋼柱損傷程度的P-I曲線圖，如圖4所示。圖中每條P-I曲線分別對應DCOL=0.2、DCOL=0.5和DCOL=0.8。

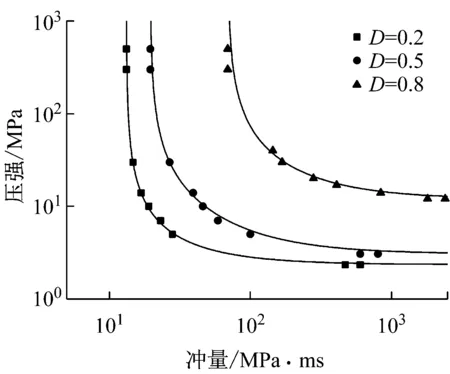
圖4 約束鋼柱在爆炸荷載作用下的P-I曲線圖Fig.4 The P-I diagram for restrained steel column

通過對數據點的擬合，P-I曲線近似滿足關系式(8)。

(8)

式中：P0和I0分別為P-I曲線超壓漸近線和沖量漸近線所對應的極限壓強和極限沖量；μ和β為2個控制曲線形狀的無量綱參數。

分別選擇ρ=τ=0.2、ρ=τ=0.3和ρ=τ=0.4三種情況，分析超壓時程曲線形狀對約束鋼柱P-I曲線的影響。經過對大量數值結果的統計分析可知，參數β基本不變，近似取β=1.78。參數μ隨超壓時程曲線形狀及損傷指數而變化，如表3所示。由表可知，對于相同的損傷指數，μ與ρ(τ)的乘積基本為一定值。

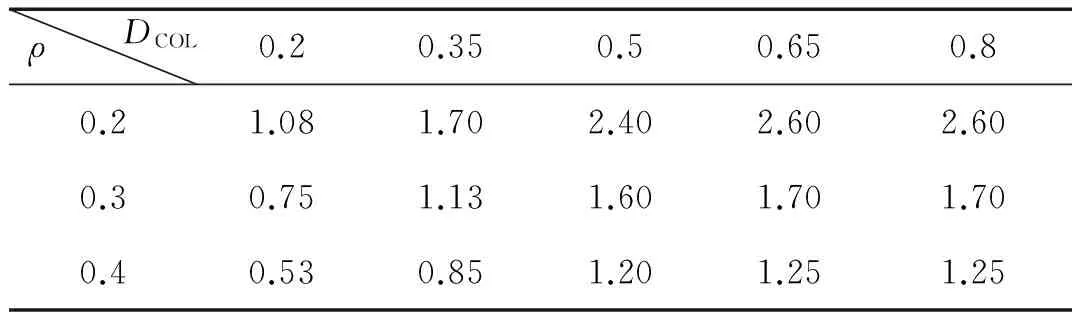
表3 不同ρ和DCOL對應的參數μTab.3 Parameter μ values for different ρ and DCOL

沖量爆炸荷載作用下，鋼柱的損傷不隨沖量荷載的形狀而變化。準靜態爆炸荷載作用下，鋼柱達到最大響應的時間遠小于爆炸沖擊荷載的持續時間，荷載形狀對鋼柱損傷的影響亦不大。因此，P-I曲線的極限壓強和極限沖量基本不受室內爆炸荷載超壓時程曲線形狀的影響[15]。表4為室內爆炸荷載作用下不同損傷指數對應的極限壓強和極限沖量。

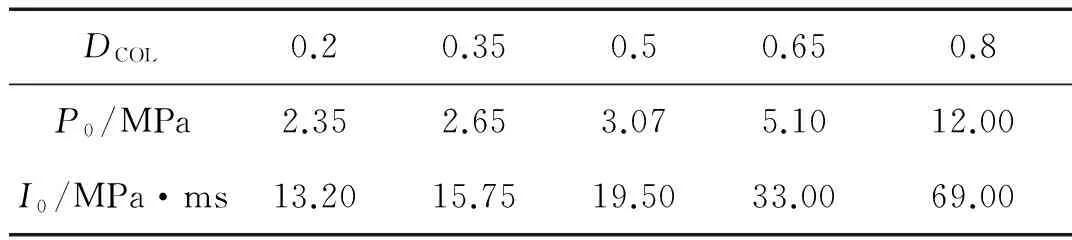
表4 不同損傷指數對應的極限壓強和沖量Tab.4 Limit pressure and impulse for different damage indexs

圖5顯示了不同超壓時程曲線形狀下、損傷指數相同約束鋼柱的P-I曲線。由圖可知，室內爆炸超壓時程曲線的形狀不同，相同損傷指數的P-I曲線的形狀不同，但影響只發生在動力荷載區域。形狀參數ρ(τ)越大，相同壓強下約束鋼柱發生同等損傷所需的沖量越小，鋼柱越易破壞。

3 爆炸荷載作用后約束鋼柱抗火分析

3.1 約束鋼柱抗火分析

火災是爆炸后常見的次生災害，鋼材的耐火性差，在爆炸荷載作用下未破壞的鋼柱往往會在次生火災作用下發生破壞。為了研究爆炸荷載作用后約束鋼柱的抗火性能，定義軸力恢復至初始值時對應的時間，為鋼柱在爆炸與火災聯合作用下的破壞時間[16]。為方便研究，采用ISO834標準火災升溫曲線表征火災場空氣升溫情況。約束鋼柱未進行防火處理，考慮鋼柱一側與墻壁相連，按三面受火對鋼柱進行熱分析，結果表明，鋼柱沿軸向溫度均勻分布，沿截面方向存在溫度梯度。隨后，將熱分析得到的溫度場引入結構分析，實現熱分析與力學分析的順序耦合[17]，最終得到鋼柱軸力隨時間變化的關系曲線，并將軸力恢復至初始值時對應的時間確定為鋼柱破壞時間。

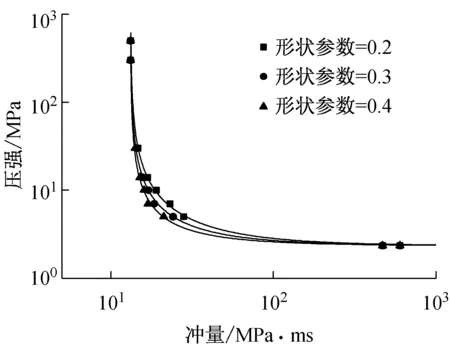
(a) DCOL=0.2

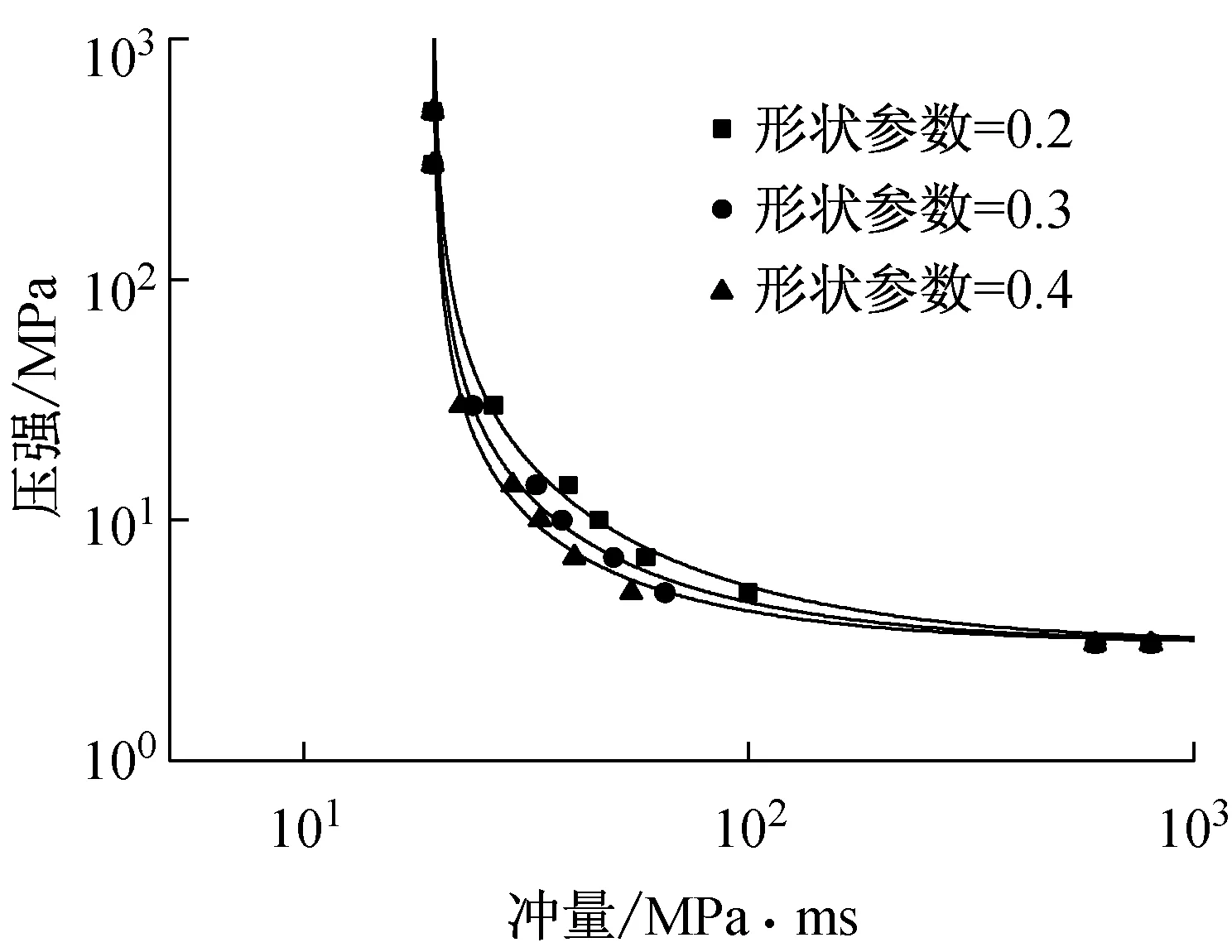
(b) DCOL=0.5

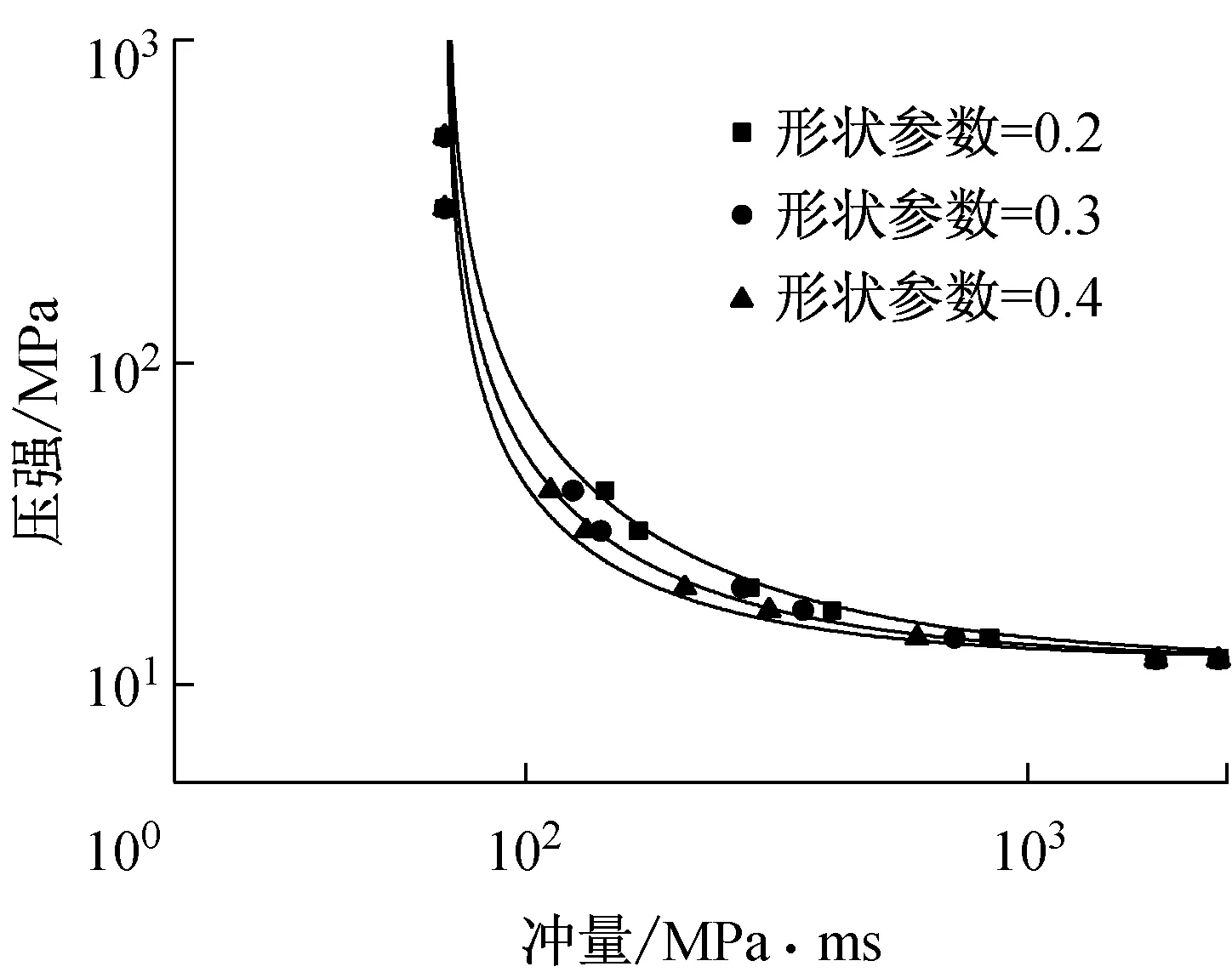
(c) DCOL=0.8

式(8)已給出了P-I曲線的一般表達式，為了將二維曲線拓展到三維的壓力-沖量-時間空間中，需得到式(8)中4個關鍵參數P0、I0、μ和β與破壞時間t之間的關系。通過大量的數值模擬和統計分析可知，參數β的值基本不受破壞時間的影響，而參數μ、P0和I0的值隨破壞時間而變化，如圖6所示。通過對數據的回歸分析，得到P0和I0與破壞時間t之間的關系滿足式(9)和式(10)，參數μ與破壞時間t及爆炸荷載超壓時程曲線形狀參數ρ(τ)之間的關系滿足式(11)。

(9)

(10)

(11)

將式(9)～(11)代入式(8)，可得到：

(12)

F(P,I,t)=0

(13)

(14)

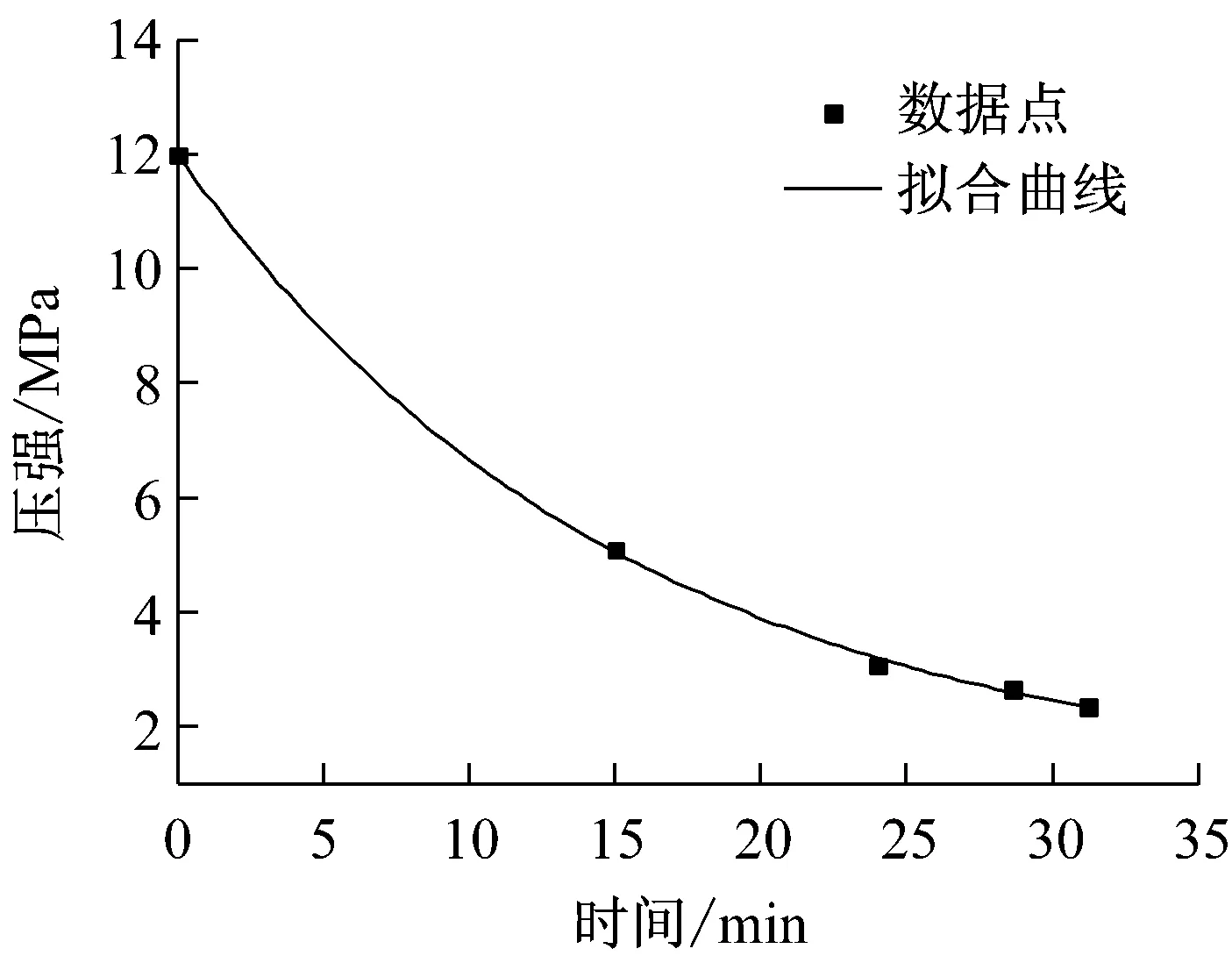
(a) P0-t

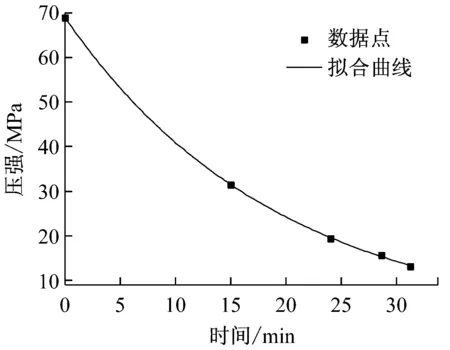
(b) I0-t

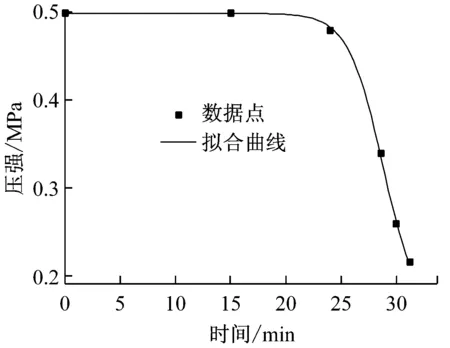
(c) μ-t

上述分析可知，超壓時程曲線的形狀參數越大，鋼柱越易破壞。偏于保守的選擇ρ(τ)=0.4的情況繪制約束鋼柱在爆炸與火災聯合作用下的P-I-t曲面圖，如圖7所示。由圖可知，建立的P-I-t曲面圖可用于約束鋼柱在爆炸與火災聯合作用下的破壞評估。

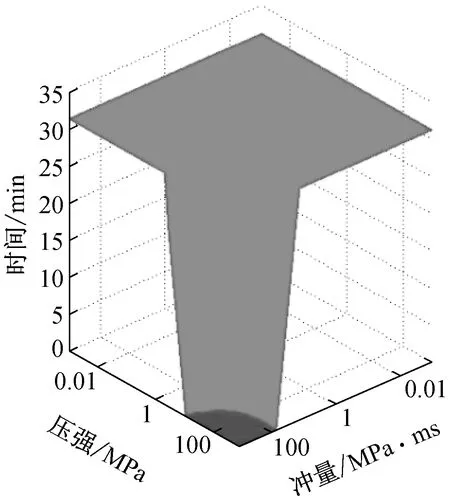
圖7 爆炸與火災聯合作用下約束鋼柱P-I-t曲面圖Fig.7 Pressure-Impulse-time diagram of restrained steel column under blast and fire

3.2 與無約束鋼柱對比

為了說明結構提供的約束對鋼柱響應的影響，首先計算了無約束鋼柱在爆炸作用下的P-I曲線圖，并與約束鋼柱結果進行對比，如圖8(a)所示。由圖可知，相同強度的爆炸荷載作用下，約束鋼柱的損傷指標小于無約束鋼柱，結構約束顯著提高了鋼柱的抗爆性能。

然而，約束的存在會降低鋼柱在純火災下的抗火性能。為了進一步說明約束對爆炸與火災聯合作用后鋼柱性能的影響，將不同爆炸損傷的約束與無約束鋼柱在火災下的破壞時間進行對比，如圖8(b)所示。由圖可知，結構約束對鋼柱在爆炸與火災聯合作用下破壞時間的影響與爆炸荷載強度有關。當無爆炸作用或爆炸產生的損傷較小時，熱膨脹產生的附加軸力導致約束鋼柱的破壞時間早于無約束鋼柱；當爆炸產生的損傷較大時，鋼柱側向變形較大，由熱膨脹引起的鋼柱軸向變形較小，因此約束鋼柱受到的附加軸力較小。由于存在屈曲后強度，約束鋼柱的破壞時間晚于無約束鋼柱。由此可見，在進行爆炸與火災聯合作用下鋼柱破壞分析時，應按真實情況考慮結構對鋼柱的約束作用。

4 影響因素分析

4.1 約束剛度影響

分析可知，改變結構中梁柱尺寸得到的不同柱端約束剛度對爆炸荷載下鋼柱響應的影響較小。因此在進行結構提供的約束剛度對P-I-t曲面圖影響分析時，本文采用改變框架層數的方法得到不同的軸向及轉動約束剛度。由第一節的分析可知，不同層數的框架在爆炸荷載作用下對鋼柱提供的約束剛度相同，只在火災分析時提供不同的約束剛度。通過數值計算，分別采用軸向約束剛度比[18]為0.015、0.035和0.052三種情況進行分析。圖9給出了爆炸荷載作用后不同損傷指標鋼柱的抗火分析時破壞時間與軸向約束剛度比之間的關系。由圖可知，僅當爆炸對鋼柱產生的損傷較大時，破壞時間會隨軸向約束剛度比的增大而出現小幅減小。因此可以認為在此種軸壓比條件下，由于考慮了鋼柱的屈曲后性能，約束剛度對爆炸與火災聯合作用下鋼柱的破壞時間基本沒有影響[19]。

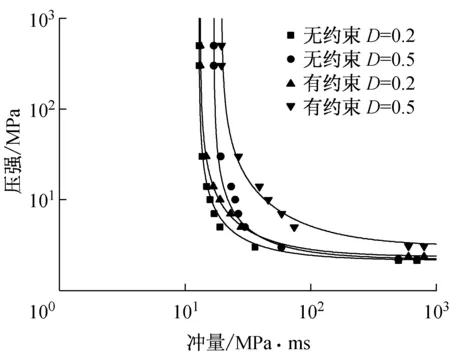
(a) P-I曲線

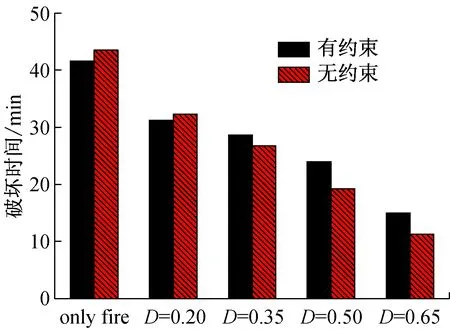
(b) 破壞時間

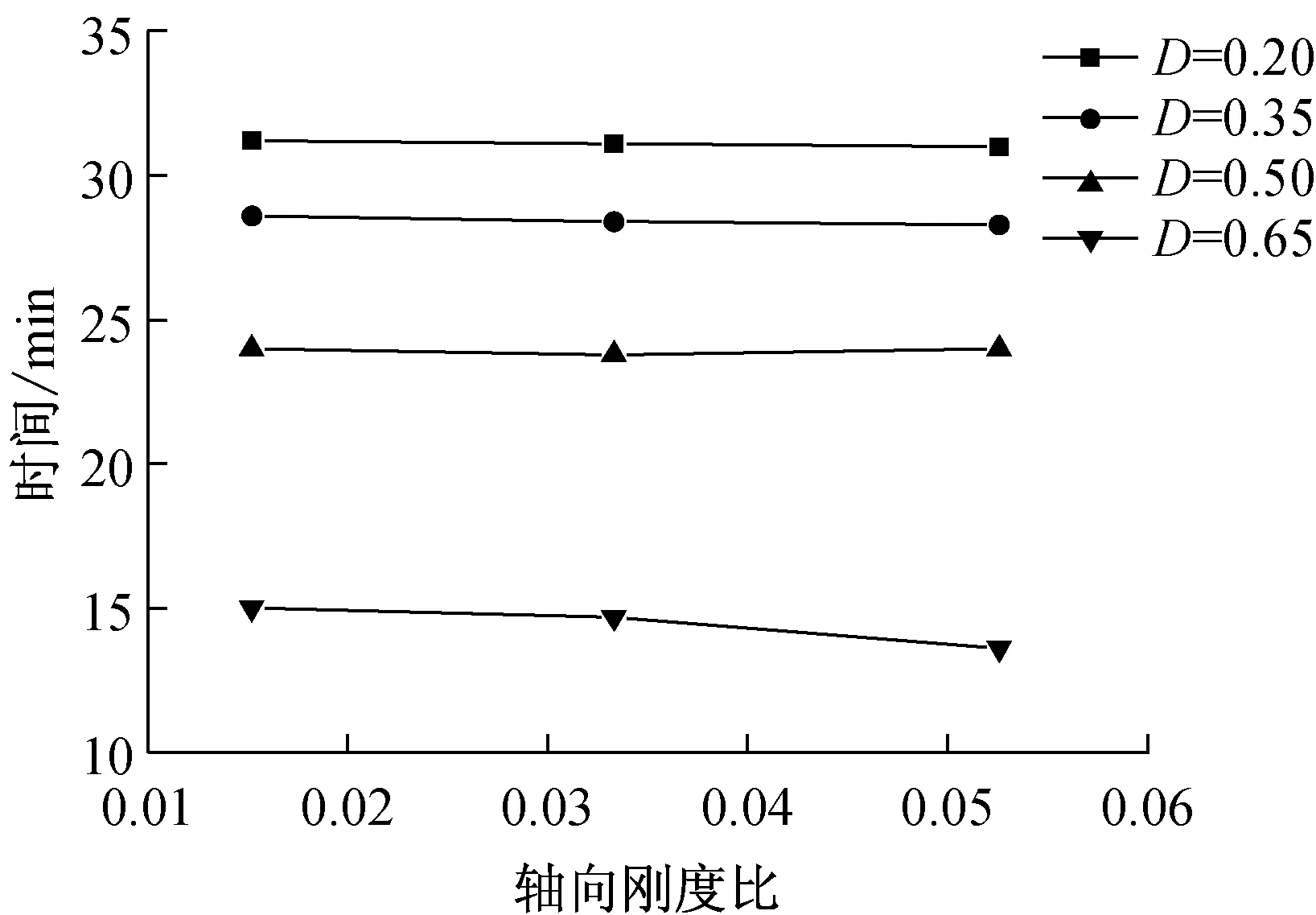
圖9 約束剛度對鋼柱破壞時間的影響Fig.9 Effects of restraint stiffness on failure time of steel column

4.2 約束鋼柱高度影響

由上述分析可知，約束剛度對鋼柱在爆炸與火災聯合作用下的破壞時間影響不大。因此在后續分析中，柱端約束剛度取定值。其他條件不變，約束鋼柱的柱高分別取3.0 m、3.6 m和4.2 m，采用上述方法分析不同柱高下約束鋼柱在爆炸與火災聯合作用下的破壞情況。分析發現，柱高越高，爆炸下產生相同損傷所需的壓強和沖量越小，且對于爆炸后損傷指數相同的鋼柱，柱高越高，在火災下發生破壞的時間越早。綜合上述分析并結合P-I-t曲面圖可知，隨著柱高的增加，約束鋼柱在爆炸與火災聯合作用下越易發生破壞，如圖10所示。

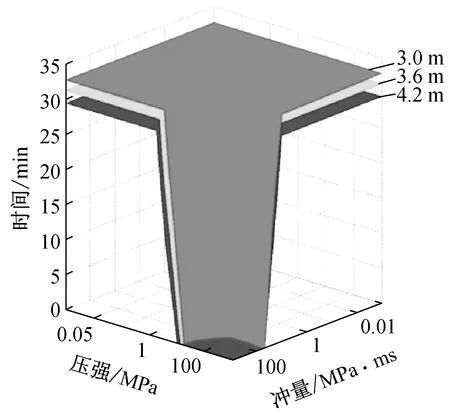
圖10 不同柱高下約束鋼柱的P-I-t曲面圖Fig.10 Pressure-Impulse-time diagram of restrained steel column under different heights

4.3 約束鋼柱壁厚影響

其他條件不變，約束鋼柱的壁厚分別取16 mm、20 mm和25 mm來分析不同壁厚下爆炸與火災聯合作用下約束鋼柱的破壞情況，并繪制P-I-t曲面圖。分析發現，當爆炸對鋼柱產生的損傷較小時，壁厚對火災下破壞時間的影響很小，如圖11中頂部區域所示。原因是增加壁厚雖然一定程度上提高了鋼柱承載力，但面積的增加同時導致附加軸力的增大，二種作用相抵使抗火時間基本不變。

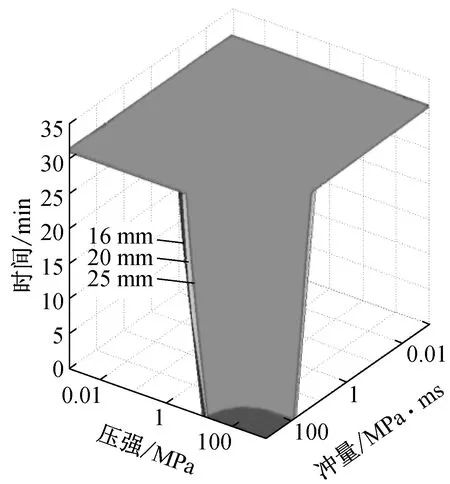
圖11 不同壁厚下約束鋼柱的P-I-t曲面圖Fig.11 Pressure-Impulse-time diagram of restrained steel column under different thicknesses

當爆炸對鋼柱產生的損傷較大時，壁厚越大，爆炸產生相同損傷指數所對應的鋼柱整體變形越大，抗火分析時的P-Δ效應越明顯。由于鋼柱截面的局部變形嚴重，厚度對承載力的提高作用弱于P-Δ效應的影響，從而導致相同爆炸損傷下，壁厚越大的鋼柱在火災下發生破壞的時間越早。但相同損傷指標下，不同壁厚鋼柱對應的P-I曲線位置不同，因此在整個壓力-沖量-時間空間下，仍是壁厚越小的約束鋼柱越容易發生破壞，如圖11所示。

4.4 約束鋼柱P-I-t曲面圖預測式

任一確定的P-I-t曲面圖僅能評估某特定幾何尺寸約束鋼柱在爆炸與火災聯合作用下的破壞情況。為了使P-I-t曲面計算式更具普適性，本文在大量數值模擬的基礎上，通過回歸分析，得到了式(8)和式(10)中各控制參數與鋼柱高度H和壁厚ts之間的關系滿足式(15)～式(24)。

(15)

(16)

(17)

(18)

(19)

(20)

B1=0.5

(21)

(22)

(23)

(24)

利用式(15)～(24)可計算出不同幾何尺寸鋼柱的曲面控制參數值，再將其代入式(12)～(14)，可得到P-I-t曲面計算式，并繪制出評估約束鋼柱在爆炸與火災聯合作用下破壞情況的P-I-t曲面圖。

5 結 論

(1) 與無約束鋼柱相比，約束鋼柱在爆炸損傷較小情況下的抗火承載力較弱，但在爆炸損傷較大情況下的抗火承載力較強。因此，在進行爆炸與火災聯合作用下鋼柱破壞分析時，應按實際情況考慮結構約束的影響。

(2) 室內爆炸荷載超壓時程曲線的形狀參數越大，約束鋼柱在爆炸作用下越易發生破壞。約束剛度對鋼柱在爆炸與火災聯合作用下的破壞時間基本沒有影響。當爆炸損傷較小時，壁厚對破壞時間影響很小；當爆炸損傷較大時，壁厚越大，鋼柱越易破壞，但在壓力-沖量-時間空間中，仍為壁厚越小、柱高越高的鋼柱越易破壞。

(3) 提出的約束鋼柱P-I-t曲面計算式可用于評估不同尺寸約束鋼柱在爆炸與火災聯合作用下的破壞情況。

[1] LIEW J Y R, CHEN H.Explosion and fire analysis of steel frames using fiber element approach[J].Journal of Structural Engineering,2004,130(7):991-1000.

[2] CHEN H, LIEW J Y R.Explosion and fire analysis of steel frames using mixed element approach[J].Journal of Engineering Mechanics,2005,131(6):606-616.

[3] LIEW J Y R.Survivability of steel frame structures subjected to blast and fire[J].Journal of Constructional Steel Research,2008,64(7/8):854-866.

[4] 閻石, 齊寶欣, 辛志強, 等.高溫與爆炸作用下輕鋼柱動力響應與破壞模式數值分析[J].土木工程學報,2010, 43(增刊1):484-489.

YAN Shi, QIN Baoxin, XIN Zhiqiang, et al.Numerical analysis on dynamic response and failure mode of light steel column under elevated temperature and blast loading[J].China Civil Engineering Journal, 2010, 43(Sup1): 484-489.

[5] 方秦, 趙建魁, 陳力, 等.爆炸與火荷載聯合作用下鋼柱變形與破壞的數值分析[J].解放軍理工大學學報(自然科學版),2013,14(4):398-403.

FANG Qin, ZHAO Jiankui, CHEN Li, et al.Numerical simulation of deformation and failure of steel columns subjected to blast and fire[J].Journal of PLA University of Science and Technology (Natural Science Edition), 2013, 14(4): 398-403.

[6] DING Yang, WANG Ming, LI Zhongxian, et al.Damage evaluation of steel tubular column subjected to explosion and post-explosion fire condition[J].Engineering Structures,2013,55:44-55.

[7] SIMMS W I, O’CONNOR D J, ALI F, et al.An experimental investigation on the structural performance of steel columns subjected to elevated temperatures[J].Journal of Applied Fire Science,1996,5(4):269-284.

[8] LI Guoqiang, WANG Peijun, WANG Yongchang.Behaviour and design of restrained steel column in fire, Part 1: Fire test[J].Journal of Constructional Steel Research,2010,66(8/9):1138-1147.

[9] 李國強, 孫建運, 王開強.爆炸沖擊荷載作用下框架簡化分析模型研究[J].振動與沖擊,2007,26(1):8-13.

LI Guoqiang, SUN Jianyun, WANG Kaiqiang.Research on a simplified frame column model to resist blast load[J].Journal of Vibration and Shock, 2007, 26(1): 8-13.

[10] 楊濤春.爆炸荷載下鋼柱破壞機理及其對框架連續倒塌影響研究[D].上海,同濟大學,2013

[11] Structures to resist the effect of accidental explosions:UFC-3-340-02[S].America: Department of the Army,Navy and the Air Force,2008.

[12] Fire-resistance tests-elements of building construction-Part:1: General requirements:ISO834-1[S].Geneva: International Standard ISO834,1999.

[13] European Committee for Standardization.Eurocode3: Design of steel structures, Part1-2: General rules-structural fire design[S].Brussels: European Committee for Standardization,2005.

[14] SHI Yangchao, HAO Hong, LI Zhongxian.Numerical derivation of pressure-impulsise diagrams for prediction of RC column damage to blast loads[J].International Journal of Impact Engineering,2008,35(11):1213-1227.

[15] JONATHON D, WU Chengqing, KATE V.Pressure-impulse diagrams for an elastic-plastic member under confined blasts[J].International Journal of Protective Structures, 2013,4(2):143-162.

[16] FRANSSEN J M.Failure temperature of a system comprising a restrained column submitted to fire[J].Fire Safety Journal, 2000,34(2):191-207.

[17] 王景玄, 王文達.考慮火災全過程的鋼管混凝土平面框架受力性能分析[J].振動與沖擊,2014,33(11):124-130.

WANG Jingxuan, WANG Wenda.Mechanical behavior analysis of a planar frame with concrete-filled steel tubular columns exposed to overall stage fire[J].Journal of Vibration and Shock, 2014, 33(11): 124-130.

[18] SHEPHERD P G, BURGESS I W.On the buckling of axially restrained steel columns in fire[J].Engineering Structures, 2011,33(10):2832-2838.

[19] 王培軍, 李國強.軸向約束鋼框架柱火災升溫下屈曲后性能研究[J].同濟大學學報(自然科學版), 2008,36(4):438-443.

WANG Peijun, LI Guoqiang.Post-buckling behavior of axially restrained steel columns in fire[J].Journal of Tongji University(Natural Science), 2008, 36(4): 438-443.

Damage evaluation of a restrained steel column subjected to indoor blast and fire

DING Yang1,2, CHEN Ye1, SHI Yanchao1,2

(1.School of Civil Engineering, Tianjin University, Tianjin 300072, China; 2.Key Laboratory of Coast Civil Engineering Structures Safety, Ministry of Education Tianjin 300072, China)

The restraint stiffness and additional mass provided by a structural system obviously influence the dynamic response of a steel column under blast, while the additional arial force induced by the restrained thermal expansion makes the capacity of restrained steel column different from that of a non-restrained column in fire.Here, Johnson-Cock damage model was used to analyze the damage of a restrained steel column under indoor blast, and the pressure-impulse-time curred surface plot and expression were established to evaluate the failure of the restrained steel column under blast and fire.To investigate the effect of restraint, the failure time of a non-restrained steel column under blast and fire was compared with that of the same column restrained.Furthermore, the parametric analysis were performed to study the effect of pressure time curved shape, restraint stiffness and geometric size on the P-I-t curved surface plot.The results showed that the failure time of the restrained steel column is earlier than that of the non-restrained steel column when the blast load intensity is smaller, while the former is later than the latter when the blast load intensity is larger; the bigger the shape parameters of pressure time history curve, the easier the restrained steel column failure; the effect of restraint stiffness on the failure time of the column can be neglected; the column wall thickness has a slight influence on the failure time when the blast induced damage is smaller, while the column with a thicker wall becomes weaker when the damage is larger; however, in the P-I-t space, the smaller the wall thickness of the column, the easier the failure of the higher column.

blast; fire; restrained steel column; damage evaluation; parametric analysis

國家“十二五”科技支撐計劃課題(2012BAJ07B05)；國家自然科學基金(50118306；51238007；51522808)

2015-09-21 修改稿收到日期：2016-01-19

丁 陽 女，教授，1966年生

師燕超 男，副教授，1982年生

TU391；TU352.5

A

10.13465/j.cnki.jvs.2017.05.013