基于灰色殘差修正理論的目標航跡預測方法

邸憶， 顧曉輝， 龍飛

(1.南京理工大學 機械工程學院， 江蘇 南京 210094； 2.貴州大學 智能信息處理研究所， 貴州 貴陽 550025)

基于灰色殘差修正理論的目標航跡預測方法

邸憶1， 顧曉輝1， 龍飛2

(1.南京理工大學 機械工程學院， 江蘇 南京 210094； 2.貴州大學 智能信息處理研究所， 貴州 貴陽 550025)

針對灰色理論在智能反坦克子彈藥對地面目標航跡預測的精度問題，提出兩種灰色殘差修正的航跡預測模型：標準灰色殘差修正模型(GRMM)和基于灰色Verhulst模型理論的灰色Verhulst殘差修正模型(GVRMM)。建立目標航跡灰色預測模型，并分析了灰色模型的局限性；對預測值與測量值的殘差序列采用GRMM和GVRMM兩種模型進行了在線預估，并利用殘差預測值對航跡預測值進行實時修正。通過仿真實驗驗證了基于在線殘差修正機制的方法能夠有效減少目標跟蹤誤差，GVRMM的誤差修正效果更加明顯，具有良好的實用性。

兵器科學與技術； 目標跟蹤； 航跡預測； 殘差修正； 灰色殘差修正模型

0 引言

智能反坦克(BAT)子彈藥是一種新型智能彈藥系統，主要在彈體飛行過程中采用聲/紅外等被動式復合探測手段對地面裝甲目標進行自動搜索、識別定位、航跡預測直至摧毀。BAT子彈藥關鍵技術是目標探測識別及快速跟蹤，通過彈載探測裝置實時探測彈目相對距離、方位角和俯仰角，再由測量信息準確預測目標航跡。

在傳統目標跟蹤航跡預測中，最常用的估計方法為卡爾曼濾波、粒子濾波及其改進算法[1-2]，通常需建立目標航跡模型和測量模型，通過測量值和狀態值的不斷迭代進行目標航跡預測和狀態預估。此類算法在現代火控系統、主動雷達跟蹤系統中表現出了良好的性能，但是在BAT子彈藥被動探測及彈載跟蹤系統中，卡爾曼濾波、粒子濾波等算法的計算復雜度很可能超出系統承載能力，并不能實現良好的預測性能。對于運動目標跟蹤而言，不同的目標運動模式需要選取相應的跟蹤模型，基于多模型假設的目標跟蹤方法[3-4]可以很好地解決機動目標跟蹤問題，而多模型假設目標跟蹤方法涉及模型集構建和模型選擇，并且傳統算法大多依賴充足的先驗知識或測量數據，不能滿足彈藥對目標跟蹤的靈活性要求。因此，針對BAT子彈藥的目標跟蹤系統迫切需要一種數據量要求較低，計算速度快，航跡預估精度良好的預測算法。

灰色理論[5]是由國內著名學者鄧聚龍教授最早提出的一門涉及多學科的數學理論系統，已在民用及軍事裝備等領域[6-8]得到了廣泛的應用。文獻[7]將一種優化的灰色模型與信息融合理論相結合，并在導彈裝備預測中取得較好的效果；文獻[8]首次將灰色預測理論引入到反直升機智能雷探測跟蹤系統，給出一種基于灰色理論的直升機航跡預估方法，實現了在少數據、貧資料狀況下的直升機飛行航跡預估。然而對于在線連續時序預測問題，傳統灰色系統理論本身的穩定性表現并不盡如人意，因此，出現了相關有針對性的改進方法[9-12]。本文首先對傳統灰色模型GM(1,1)本身的局限性進行了分析；其次，針對傳統算法的缺陷及誤差問題，并未進行算法本身的改進，而是在灰色模型中引入在線殘差修正策略，建立了兩種殘差修正預測模型：標準灰色殘差修正模型(GRMM)和灰色Verhulst殘差修正模型(GVRMM)，可快速更新航跡預測值，防止目標跟蹤過程中的誤差累積，進一步提升預測精度，對于目標航跡預測有著積極的理論參考和工程應用價值。

1 灰色航跡預估模型

設原始測量數據列[8]為

{x(0)(i)}，i=1,2,…,N，

(1)

式中：x(0)(i)可以表示為BAT彈體與目標之間的徑向距離、方位角或者俯仰角測量值。

一次累加生成算子(AGO)序列

{x(1)(i)}，i=1,2,…,N，

(2)

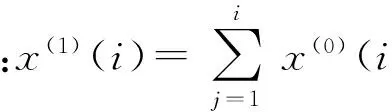
建立GM(1,1)模型：

(3)

參數列為

(4)

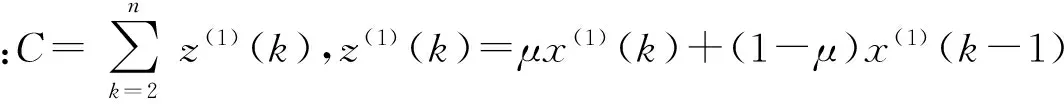
計算離散解有

(5)

經逆向推導，由一次累加可還原預測值：

(0)(k)=(1)(k)-(1)(k-1).

(6)

在線實時預測就是用N個原始探測數據建立以上GM(1，1)模型，并預測下一時刻的預測值。而隨著探測系統的掃描，得到下一時刻的測量值后，則放棄原數據列中的初值，選取最新測量值，形成新的數據列{x(0)(i)}(i=2，…，N+1)，重新建立GM(1，1)模型，如此進行循環迭代，實現目標航跡的實時預測。

2 灰色預估模型缺陷分析

基于灰色理論的目標航跡預測模型簡單，計算簡便，但GM(1,1)自身存在不足：

1)背景值鄰值權系數μ定義的盲目性[10]。背景值的構造控制是灰色模型預測誤差控制的關鍵，如(4)式中背景值z(1)(k)的構造過程中，一般其鄰值權系數μ=0.5，而μ的定義直接影響到發展系數a以及灰作用量b的確定。更進一步，GM(1,1)模型的預測精度則取決發展系數a和灰作用量b，因此背景值鄰值權系數μ取值為0.5存在一定的盲目性，不能保證模型預測結果達到最佳。

基于灰色理論的目標跟蹤航跡預測模型是微分方程模型，摒棄大量樣本的統計特性研究，而是將所有信息統一為灰色過程，通過累加生成弱化序列中數據的隨機性，生成規律較強的數列，因此很容易實現少數據、貧資料狀況下的目標狀態預測。盡管對灰色理論本身缺陷進行了針對性的改進，但一直無法徹底擺脫其局限性，大多在原有基礎上盡可能提高灰色模型的擬合精度，那么在基于灰色理論的目標航跡預測中，將研究重心從算法本身轉移到誤差補償，不失為一種有效的途徑。

3 灰色殘差修正模型

在BAT子彈藥對地面目標跟蹤航跡預測中，彈載跟蹤系統的飛行、環境干擾、測量系統誤差以及目標的運動狀態突變均不能保證原始數據的準確性。那么，在線目標跟蹤及航跡更新若僅依賴于傳統灰色模型的少數據迭代外推思想，可能造成計算誤差累積效應，最終導致目標跟蹤失敗。針對該問題，本文采取的解決方案是在灰色理論的基礎上引入殘差修正機制，建立標準GRMM和GVRMM用于解決目標跟蹤過程中由于算法局限性造成的航跡預測誤差累積的問題。

3.1 標準灰色殘差修正模型

設第k時刻預測值與原始累加值的殘差為

(7)

得到一次修正估計值：

(8)

(9)

可得

(10)

11月7日，麗江和迪慶供電局應急指揮中心就已布置完畢，啟動了24小時應急值班制。兩個供電局分別與當地水務部門建立了聯動機制，安排專人實時獲取水文信息，及時開展險情分析研判工作。

建立n次累加m次GRMM：

(11)

(12)

可得

(13)

設殘差參數列為

(14)

辨識算式為

Δm(n)=
[Δ(A?B),Δ(A?B)]-1Δ(A?B)y(Δ(n-1))，

(15)

得到離散解為

(16)

該模型是一種嵌套式灰色模型，先由灰色模型得到目標航跡預測值序列，進而得出殘差序列，再對殘差序列進行灰色模型建模計算，與預測值相加得出更加逼近真值的預測結果。因此，GRMM和GM(1，1)模型一樣需要同時在線進行，達到目標跟蹤及誤差實時修正的目的，可有效提升目標跟蹤精度。

3.2 灰色Verhulst殘差修正模型

GVRMM[13]是灰色模型的改進形式，在解決具有飽和“S”型預測問題時具有良好的效果。通過研究發現[14]，BAT在飛行過程中對地面目標的航跡預測殘差在目標的機動動作及其他干擾情況下可以認為具有飽和的近似“S”型序列，那么采用GVRMM對目標航跡預測殘差進行建模及修正則顯得更加合理。

航跡殘差計算如(7)式～(10)式所示，建立n次累加m次GVRMM：

(17)

(18)

可得

(19)

設殘差參數列

(20)

辨識算式為

Δm(n)=
[Δ(A?B),Δ(A?B)]-1Δ(A?B)y(Δ(n-1))，

(21)

得到離散解為

(22)

4 計算實例

圖1 BAT子彈藥對地目標跟蹤示意圖Fig.1 Schematic diagram of tracking a target by BAT submunition

以BAT子彈藥對地面目標跟蹤為例，選用BAT子彈藥相對目標的徑向距離r作為目標跟蹤參量，如圖1所示，設BAT在空中以100 m/s的速度逼近目標，目標的先以12.5 m/s的速度運動，在某一時刻開始以的3.4 m/s2加速度進行加速運動，彈目初始距離330 m，以每0.1 s的徑向距離探測值作為原始數據，選取最初5個數據點(見表1)，首先進行GRMM和GVRMM建模和一步預測。

表1 BAT子彈藥對地目標徑向距離原始數據Tab.1 Radial distance between BAT submunition and target

將表1數據帶入文獻[8]所提的傳統GM(1,1)模型得

(1)(k)=-11 343.081 7e-0.028 796(k-1)+
11 673.0817，k≥1.

經過2次累加1次殘差修正的GRMM模型為

(1)(k)=0.199 0e-0.752 9(k-1)-0.199 0，k≥1.

經過2次累加1次殘差修正的GVRMM模型為

(1)(k)=0.635 6e-0.635 633(k-1)，k≥1.

當彈載測距裝置測得k=6時的彈目徑向距離為286.321 4 m時，拋去原數據列中首值，重新建立航跡預估模型及殘差修正模型，得到GM(1,1)模型為

(1)(k)=-8 718.388 9e-0.032 392(k-1)+9 004.710 3，
k≥1.

經2次累加1次殘差修正的GRMM模型為

(1)(k)=0.035 3e-0.436 633(k-2)-0.035 3，k≥2.

2次累加1次殘差修正的GVRMM模型為

(1)(k)=0.714 4e-0.714 360(k-2)，k≥2.

再由(10)式即可得到經m次殘差修正后的1次累加預測值。

定義殘差均值為

(23)

由表1數據計算得到：基于傳統GM(1,1)徑向距離預測誤差為0.145 1 m，誤差方差為0.034 4 m2；而GRMM徑向距離預測誤差為0.123 9 m，誤差方差為0.010 1 m2；GVRMM徑向距離預測誤差為0.061 9 m，誤差方差為0.028 6 m2. 當彈載測距裝置測得k=6時的彈目徑向距離為286.321 4 m時，新數據列計算結果為：基于GM(1,1)徑向距離預測誤差為0.138 3 m，誤差方差為0.023 6 m2；而GRMM徑向距離預測誤差為0.131 4 m，誤差方差為0.011 3 m2；GVRMM徑向距離預測誤差為0.058 3 m，誤差方差為0.029 2 m2.

定義相對偏差百分比(RPE)為

(24)

定義平均相對偏差比(ARPE)為

(25)

再對目標進行全局在線觀測及航跡預測，總觀測時長為1 000 ms，采樣頻率為100 Hz，分別建立基于GRMM和GVRMM的全局航跡預測模型并計算預測結果。圖2給出了兩種灰色預估模型的估計值以及文獻[8]所提GM(1，1)的估計值，圖3為260～320 ms的局部放大圖。從圖2中可以清楚地看到，GVRMM的航跡值最接近真實值，其次為GRMM模型預估值，而非修正GM(1，1)模型預測結果的相對其他兩種模型的預估結果較差。

圖2 真實彈目距離及不同模型預測結果Fig.2 Real projectile-target distances and predicted results of different models

圖3 260～320 ms時的真實彈目距離及不同模型預測結果Fig.3 Real projectile-target distances data and predicted results of different models in the time range from 260 to 320 ms

圖4顯示了不同模型全局在線預測的相對偏差，從圖4中不難發現：GM(1，1)航跡預測模型的偏差較大，且波動幅度較大；GRMM和GVRMM預測偏差均較小，而GVRMM偏差最小。圖5和圖6給出了3種模型預測值的最小均方誤差和相對偏差比RPE曲線，可以發現，灰色殘差修正航跡預測模型的誤差要明顯小于未修正灰色航跡預估模型。

圖4 目標航跡預測偏差Fig.4 Predicted track errors of different models

圖5 目標航跡預測均方誤差Fig.5 MSEs of predicted target tracks

圖6 目標航跡預測相對偏差百分比Fig.6 RPEs of predicted target tracks of different models

計算3種模型所對應的ARPE(見表2)分別為：0.121 1、0.089 9和0.059 1. 由此驗證了基于灰色殘差修正理論的目標航跡預測精度優于未修正模型航跡預測精度，其中GVRMM精度最優。值得注意的是，傳統GM(1，1)模型耗時最短為0.156 s，而本文所提的GRMM模型與GVRMM模型耗時分別為0.228 s和0.226 s，原因在于GRMM和GVRMM計算過程中在GM(1，1)的基礎上額外增加了殘差預估和修正，從而計算復雜度上增加了兩次累加過程，但每次迭代時間遠小于傳感器測量一次的時間，因此認為本文所提兩種算法仍然符合BAT子彈藥對地目標跟蹤的實時性要求。

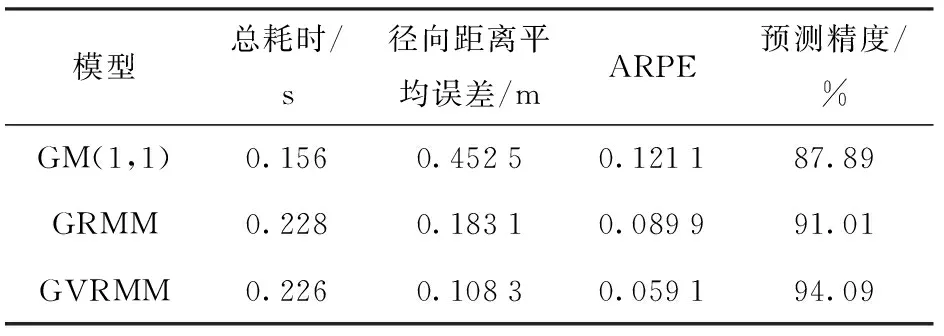
表2 3種模型全局預測性能對比Tab.2 Comparison of prediction performances of three models

5 結論

針對BAT子彈藥對目標航跡預測的精度問題，提出了兩種灰色殘差修正的目標航跡預測方法。通過與傳統灰色航跡預估模型對比，本文所提的兩種殘差修正模型的航跡預測精度分別提高3.12%和6.2%，而基于灰色Verhulst估計的GVRMM航跡預測性能最優。

本文主要以彈目徑向距離為例進行了算法仿真計算，而真實探測系統還會涉及彈目方位角和俯仰角等其他參數，則多參數的灰色系統目標跟蹤算法將是下一步工作重點。

References)

[1] Kalman R E. A new approach to linear filtering and prediction problems[J]. Journal of Basic Engineering, 1960, 82(1): 35-45.

[2] Hlinomaz P, Hong L. A multi-rate multiple model track-before-detect particle filter[J]. Mathematical and Computer Modeling, 2008, 49(1): 146-162.

[3] Lan J, Li X R. Equivalent model augmentation for variable structure multiple-model estimation[J]. IEEE Transactions on Aerospace and Electronic System, 2013, 49(4): 2615-2630.

[4] 孫寶亮, 姜春蘭, 李明, 等. 基于模糊邏輯的交互式多模型網絡化彈藥多節點目標跟蹤算法[J]. 兵工學報, 2015, 36(4):595-601. SUN Bao-liang, JIANG Chun-lan, LI Ming, et al. Fuzzy logic-based interacting multiple model algorithm of networked munitions for target tracking[J]. Acta Armamentarii, 2015, 36(4):595-601. (in Chinese)

[5] Kayacan E, Ulutas B, Kaynak O. Grey system theory-based models in time series prediction[J]. Expert Systems with Applications, 2010, 37(2): 1784-1789.

[6] Kumar U, Jain V K. Time series models (Grey-Markov, Grey model with rolling mechanism and singular spectrum analysis) to forecast energy consumption in India[J]. Energy, 2010, 35(4):1709-1716.

[7] 趙建忠, 葉文, 張磊. 基于數據融合和改進新陳代謝不等間距GM(1,1)模型的導彈裝備故障預測[J]. 兵工學報, 2014, 35(10): 1689-1695. ZHAO Jian-zhong, YE Wen, ZHANG Lei. Failure prediction of missile equipment based on data fusion and AMUGM(1,1) model[J]. Acta Armamentarii, 2014, 35(10): 1689-1695. (in Chinese)

[8] 顧曉輝, 王曉鳴, 趙有守. 基于灰色系統預測直升機航跡的研究[J]. 航空學報, 2001, 22(6): 559-562. GU Xiao-hui, WANG Xiao-ming, ZHAO You-shou. Prediction of helicopter tracks based on grey system theory [J]. Acta Aeronautica et Asstronaytica Sineca, 2001, 22(6):559-562. (in Chinese)

[9] Xu J, Tan T, Tu M, et al. Improvement of grey models by least squares[J]. Expert Systems with Applications, 2011, 38(11):13961-13966.

[10] 羅黨, 劉思峰, 黨耀國. 灰色模型GM(1,1)優化[J]. 中國工程科學, 2003, 5(8):50-53. LUO Dang, LIU Si-feng, DANG Yao-guo. The optimization of grey model GM(1,1)[J]. Engineering Science, 2003, 5(8):50-53. (in Chinese)

[11] 何海, 陳綿云. GM(1, 1)模型預測公式的缺陷及其改進[J]. 武漢理工大學學報, 2004, 26(7): 81-83. HE Hai, CHEN Mian-yun. Prediction formula’s defect of GM(1,1) and its improvement[J]. Journal of Wuhan University of Technology, 2004, 26(7): 81-83. (in Chinese)

[12] 寧小磊, 吳穎霞, 于天朋,等. 基于改進灰色關聯分析的仿真模型綜合驗證方法[J]. 兵工學報, 2016, 37(2):338-347. NING Xiao-lei, WU Ying-xia, YU Tian-peng, et al. Research on comprehensive validation of simulation models based on improved grey relational analysis [J]. Acta Armamentarii, 2016, 37(2):338-347. (in Chinese)

[13] 崔立志, 劉思峰, 李智屏.灰色離散Verhulst模型[J]. 系統工程與電子技術, 2011, 33(3): 590-593. CUI Li-zhi, LIU Si-feng, LI Zhi-ping. Grey discrete Verhulst model[J]. Systems Engineering and Electronics, 2011, 33(3): 590-593. (in Chinese)

[14] 劉亞雷.三維運動聲陣列對聲目標跟蹤理論研究[D]. 南京:南京理工大學, 2013. LIU Ya-lei. Study on the tracking theory of 3D dynamic acoustic array for acoustic target[D]. Nanjing: Nanjing University of Science and Technology, 2013. (in Chinese)

Target Track Prediction Method Based on Grey Residual Modification Theory

DI Yi1， GU Xiao-hui1， LONG Fei2

(1.School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China;2.Institute of Intelligent Information Processing, Guizhou University, Guiyang 550025, Guizhou, China)

Two grey residual modification models are proposed for the track prediction precision of brainpower antitank (BAT) submunition based on grey theory, which are grey residual modification model (GRMM) and grey Verhulst residual modification model (GVRMM). A grey model of target track prediction is established, and the limitations of this model are analyzed. GRMM and GVRMM are used to correct the grey forecast model on line, respectively. It shows that the proposed method based on real-time residual modification mechanism can be used to reduce the prediction error effectively, and GVRMM has better efficiency in improving track prediction precision.

ordnance science and technology; target tracking; track prediction; residual modification; grey residual modification model

2016-05-03

國家自然科學基金項目(61263005)

邸憶(1987—), 男, 博士研究生。E-mail: diyi8710@163.com

顧曉輝(1964—), 男, 教授，博士生導師。E-mail: gxiaohui@njust.edu.cn

TJ413+.3

A

1000-1093(2017)03-0454-06

10.3969/j.issn.1000-1093.2017.03.006