考慮臨近空間零控交班的指令修正中制導研究

張浩強， 唐勝景， 郭杰， 劉驍， 徐倩

(1.北京理工大學 宇航學院 飛行器動力學與控制教育部重點實驗室， 北京 100081; 2.北京宇航系統工程研究所, 北京 100076)

考慮臨近空間零控交班的指令修正中制導研究

張浩強1， 唐勝景1， 郭杰1， 劉驍1， 徐倩2

(1.北京理工大學 宇航學院 飛行器動力學與控制教育部重點實驗室， 北京 100081; 2.北京宇航系統工程研究所, 北京 100076)

針對臨近空間高超聲速目標防御問題，根據目標特性提出了空基巡航段防御方案。在此基礎上考慮臨近空間防御特點進行中末制導交班問題分析，提出交班點性能指標，并得出連接中末制導階段的有效零控攔截交班區域(零控交班)。結合模型預測靜態規劃理論與防御飛行器中制導終端狀態約束條件，推導了最優控制問題的解析算法并將其作為防御飛行器的指令修正制導律，針對不同任務情況進行了數值仿真。仿真結果表明，零控交班區域分析結果可滿足終端小速度比交會條件。設計的中制導律在顯著提高計算效率的同時滿足零控交班約束,且經過Monte Carlo仿真表明對初值擾動具有較強的魯棒性。

兵器科學與技術； 飛行器設計； 零控脫靶量； 交班點； 模型預測靜態規劃； 中制導

0 引言

臨近空間是指傳統的航天與航空之間的空白區域，一般認為在20～100 km之間的空間領域。近年來，臨近空間特殊的戰略價值已經得到廣泛重視[1]。隨著臨近空間飛行器的快速研究與發展，臨近空間已成為國家空間戰略安全的重要組成部分[2]。因此，對臨近空間目標有效防御的研究具有重要的戰略意義。本文考慮的高超聲速飛行器是在臨近空間某高度以較穩定的速度飛行并具有一定滯空時間的巡航型飛行器，這類飛行器主要指近年來發展的吸氣式高超聲速巡航飛行器[3]。

吸氣式高超聲速巡航飛行器在其巡航段飛行時間最長，攻擊窗口最大，航跡最平穩，最容易被發現和跟蹤，因而巡航段防御是一種最有效、最理想的目標交會方式[4]。根據文獻[5]提出的空基發射防御方案，本文系統地研究了臨近空間防御飛行器中制導框架中存在的問題。

空基防御飛行器是基于成熟的中遠程空空導彈改進而成：在預警系統發現并跟蹤目標后，載機攜帶防御飛行器迅速爬升至一定高度。此后防御飛行器發射，爬升至目標高度后對目標進行攻擊。對于此類空基防御飛行器，在導引頭開機前自身無法鎖定目標，所以需要采用復合制導體制來完成目標打擊任務。

其交班點作為中制導結束點同時也是末制導啟控點，對于防御飛行器的復合制導體制起到了承前啟后的關鍵作用。文獻[6-7]從理論上研究了反臨近空間高超聲速飛行器中末制導交班需用的導引頭關鍵技術及視角選擇問題。在針對考慮臨近空間防御特點的中末制導交班點分析方面，國內外的相關文獻目前較少，并且多集中于對導引頭技術的研究，缺乏對最佳交班位置及相關約束條件的詳細討論與分析。

對于中制導體制的選取，本文選用空空導彈普遍采用的捷聯慣導+雷達指令修正中制導方案[8-9]。在防御飛行器中制導階段，針對高超聲速目標的時敏性，在線可實時優化的制導段軌跡生成算法已經成為當前研究的熱點與難點[10]。針對這一問題，本文考慮采用一種快速可在線實施的制導律作為修正指令，并由火控系統通過數據鏈實時控制飛行器軌跡。因此對此種修正制導指令進行設計與驗證，則成為臨近空間防御飛行器中制導框架中的又一個關鍵問題，亦作為本文的另一個研究重點。

最優控制理論被廣泛應用于制導律框架設計，包括針對高速來襲目標的最優指令成形制導律及帶多約束條件的時變參數次優中制導律研究等[11-12]。近年來，Padhi等[13]將模型預測控制(MPC)與近似動態規劃(ADP)相結合，提出了模型預測靜態規劃(MPSP)理論。對于最優控制中的典型兩點邊值問題，該方法只需要靜態協態矢量來更新控制量，且協態矢量可以通過使用敏感度矩陣來進行遞歸計算。目前MPSP理論已經應用到飛行器再入制導[14]、高速目標防御中制導[15]以及帶落角約束的末制導[16]，具有較好的應用價值和發展前景。

針對上述背景與問題現狀，本文考慮采用空基防御方案。在此方案背景下，考慮臨近空間高超聲速巡航飛行器飛行特點，并基于零化末制導零控脫靶量(ZEM)的設計思想，本文對中末制導零控交班區域進行討論分析；同時給出了相應的彈道及動力學約束；結合MPSP理論方法，對考慮多終端約束的指令修正中制導律進行了設計研究。

1 中制導模型

1.1 目標巡航段彈道特性分析

針對高超聲速目標，如前所述，其在巡航段飛行過程中有非常明顯的彈道特性，在此段進行防御攔截最為有效:

1)典型高度飛行。由于低空大氣密度大使得阻力較大，而過高的飛行高度又不能給發動機提供足夠的空氣，采用吸氣式超燃沖壓發動機的高超聲速飛行器，由于飛行攻角的約束限制，較適合于在約30 km高度巡航飛行。

2)臨近空間內的飛行時間較長。

3)高超聲速巡航飛行。

4)機動力較弱。臨近空間氣體稀薄，導致可用過載相對較低，尤其是吸氣式沖壓發動機的進氣道設計限制了其大攻角飛行，而巡航段的飛行器也不易實現直接力控制[5]。

1.2 彈目相對非線性運動學

彈目相對非線性運動學多建立在慣性參考坐標系下，如圖1所示。圖1中：r為導彈與目標之間的相對距離；λ為彈目視線角；v、a、γ、Φ分別表示速度、加速度、彈道傾角以及速度前置角，下標M、T分別表示導彈與目標。其運動方程為

(1)

式中：vr與vλ分別表示彈目相對速度沿彈目視線的切向分量與法向分量。

圖1 非線性運動學彈目關系Fig.1 Relationship between missile and target in nonlinear kinematics

1.3 中制導段防御飛行器數學模型

防御飛行器縱向平面的質點動力學模型(不考慮發動機推力)為

(2)

式中：xM、yM為防御飛行器在發射坐標系中的位置；D為氣動阻力；ηγ為制導指令；g為重力加速度；m為防御飛行器質量。

2 臨近空間防御中末制導交班問題分析

2.1 常規交班點性能指標分析

從制導的最終目的來看，控制終端時刻的脫靶量達到最小是末制導的一個非常重要的指標。而中末制導交班點為中制導與末制導的承接點，既作為中制導的終止點也作為末制導的啟控點，因此這一點處的彈道特點以及性能指標顯得尤為重要，對整個制導過程來說都起到了承前啟后的關鍵作用。

由于發動機和其他技術水平的限制，為了讓導彈具有一定的射程，必須考慮在長時間的中制導過程中使導彈能量消耗盡可能的少。另外，在采用慣性制導方式時，中制導過程中導彈不再獲取目標信息，這將使得不可預計的目標機動隨時間逐漸累積。在這種情況下，需要把短的飛行時間作為中制導的一個基本性能指標。

2.2 考慮臨近空間防御特點的交班點性能指標分析

1)速度約束。定義臨近空間防御飛行器在中末制導交班時刻的速度大小為vM，臨近空間高超聲速飛行器的巡航速度大小為vT，則二者速度比為：η=vM/vT，并且η一定小于1. 將這種情況定義為小速度比攻擊。同時，出于對末制導過程中機動能力的考慮，希望在交班點處防御飛行器能擁有較大的終端速度。

2)高度約束。假設在中末交班時刻彈目速度比η一定，即防御飛行器速度大小一定。在這一時刻從能量角度分析，相對于某一水平面，若防御飛行器位置高于高超聲速巡航飛行器的位置，那么在彈目終端交匯時刻防御飛行器有一部分勢能可以轉化為動能，形成俯沖攻擊從而可提供更大的可用過載。從另一個角度分析，文獻[7]研究得到的結論指出：為提高導引頭探測距離，從而增加末制導作用距離，探測視角最好采用自上而下的方式。同樣也對交班點高度約束提出了要求。

3)ZEM約束。ZEM的概念最早被應用于防御大氣層外處于自由飛行段的彈道導彈[17-19]。ZEM的物理意義是導彈從當前時刻到制導結束不再輸出制導指令，而目標仍按此前的機動方式運動，彈目直至終端時刻的脫靶量大小。本文提出零化交班時刻ZEM的思想，將交班點處的ZEM作為中制導的一個終端約束。

根據圖1所示的非線性運動關系，定義彈目相對位移矢量為R，相對速度矢量為v，v與R叉乘的模ε為零控脫靶標志量，其中δ為v與R的夾角，零控脫靶標志量的數學推導為

v×R=0，

(3)

ε=|v×R|，

(4)

ε=|v||R|sinδ=vλR.

(5)

2.3 有效零控攔截交班區域

本節主要針對提出的有效零控交班區域給出具體的分析推導過程，并據此給出相關概念的定義。為便于分析推導，作以下假設：

1)對于臨近空間高超聲速巡航目標，預警探測系統可以探測到目標的航跡點，包括航跡點位置及目標速度；

2)僅考慮防御飛行器與目標在同一縱向平面內的質心動力學情況，同時認為防御飛行器攻角α≈0°；

3)探測到航跡點的時間間隔均勻，探測周期為T；

4)tn時刻探測到的目標信息為Xn=(xn,yn,zn)，根據Xn可以預測下一時刻的目標信息Zn+1，并將tn+1作為末制導的啟控時刻；

5)如果目標在一個探測周期內發生了機動，那么在tn+1時刻進行重新探測得到該時刻的實際探測值Xn+1,并將該時刻預測的下一時刻目標信息Zn+2作為末制導的啟控點；

6)目標速度方向與參考平面平行，即彈目視線角λ與目標前置角ΦT相同。

7)防御飛行器導引頭最大探測距離為rmax，導引頭視場角為ψ(假設導引頭光軸不轉動)。

交班時刻的彈目相對位置關系如圖2所示。其中，點O1為tn+1時刻預測到的目標航跡點位置，以O1為圓心以rmax為半徑作圓O1，圓O1表示在tn+1時刻目標可被捕獲的最大范圍；O1O2表示目標當前時刻的速度矢量，以目標速度矢量的終點O2為圓心，以防御飛行器速度大小vM為半徑做圓O2(則圓O2上任意一點與點O1、點O2構成閉合的彈目速度矢量三角形)；O1A和O1B分別為圓O2過點O1的兩條切線。

圖2 零控交班區域Fig.2 Zero effort handover region

根據文獻[20]對零控攔截的定義及本文提出的假設1～假設7，結合圖2對零控交班區域展開推導與分析如下：

ΦM=arcsin (sinλ/η)，

(6)

γM=-(ΦM+λ)=-arcsin (sinλ/η)-λ;

(7)

5)根據圖2中幾何關系可知，在最大零控交班區域范圍內，對于不同的中、末制導交班點位置處的速度前置角會隨著彈目視線角的減小而逐漸減小。

(8)

由(8)式可知，影響有效零控交班區域的主要因素有兩點，分別為彈目速度比和導引頭視場角的大小。在一定范圍內，適當增大彈目速度比或者提高導引頭視場范圍，可以一定程度上增大有效零控交班區域。

另外，在考慮縱向平面質點模型的條件下，認為導引頭視場范圍即為視場錐體在參考線上投影的長度lp. 因此有效零控交班區域內不同的點會對應不同的投影長度，考慮以O1為極點的極坐標系，對有效零控交班區域內任意有限點進行曲面擬合，則有

lp=f(r,λ).

(9)

由有效零控交班區域所得的中制導終端約束條件對防御飛行器位置的約束應該是一個點。因此，曲面函數f(r,λ)的極大值點即為最佳交班位置。

3 防御飛行器中制導終端約束

中制導終端約束的確定，首先需要根據第2節的分析計算零控交班區域內不同點作為交班點時的視場投影長度，并選取投影長度極大值為最佳位置，從而以該點的動力學狀態作為終端約束，最后將該點的位置和速度信息轉換到防御飛行器發射坐標系下即可。

如圖3所示，I為末制導交班點，ri和λi分別表示ti時刻的彈目距離和彈目視線角度，hi表示當前時刻防御飛行器相對于目標的高度，li表示防御飛行器視場在這一高度參考線上的投影長度。

圖3 視場投影長度Fig.3 Projected length of field of view

根據圖3的幾何關系及(8)式可得

li=f(ri,λi)，

(10)

li=li1+li2=hitanα1+hi/tanα2，

(11)

式中：

hi=risinλi；

(12)

αi1=ψ/2+λi+ηiM-π/2；

(13)

αi2=λi+ηiM-ψ/2.

(14)

將(12)式～(14)式代入(11)式中整理可得

(15)

通過分析(15)式的極大值點(rd,λd)來確定最佳交班位置：根據(5)式的單調性可知隨著λ的逐漸減小，ηM也逐漸減小；彈目視線變化過程中的某一個位置會出現極限情況lp=∞，即防御飛行器視場一條邊界與參考線平行；如果彈目視線角繼續減小，防御飛行器高度下降但投影長度仍維持無窮大。

綜合以上分析并考慮防御飛行器高度約束，彈目視場邊界恰好與參考線平行的位置為最佳交班位置，即

(16)

極坐標(rd,λd)轉換成發射坐標(xd,yd)有

(17)

式中：(xT,yT)為目標在發射系下的坐標位置。

根據平行原理可得彈道傾角γd=-ψ/2，那么，Xd=[xd,yd,γd]T即為中制導結束時所需滿足的終端約束條件。

4 MPSP方法

Xk+1=Fk(Xk,Uk),
Yk+1=h(Xk),

(18)

式中：X為狀態變量；U為控制變量；Y為控制輸出，控制目標滿足MPSP理論的基本原理。

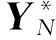
(19)

(20)

式中：HOT為高階小量。

根據(18)式，第k+1步的狀態量誤差為

(21)

將(21)式帶入(20)式可以得到第N步的輸出誤差為

(22)

繼續按照(21)式中的形式展開(22)式中的dXN-1，得

(23)

以此方式迭代求解得

dYN=AdX1+B1dU1+B2dU2+…+
BN-1dUN-1,

(24)

式中：

(25)

Bk稱為敏感度矩陣，由于在第1步迭代時初值已經給定，因此不存在狀態誤差量，即(24)式中dX1=0，則

(26)

這里需要注意，在推導(26)式的過程中，假設每一步的控制變量都獨立于前一步的狀態量與控制輸入。

由(25)式可知，敏感度矩陣的計算相當繁瑣，這將會大大影響MPSP算法的求解效率，但可以注意到，敏感度矩陣可以通過下面的推導進行反向遞歸求解：

(27)

(28)

根據(26)式及最優控制的ADP方法，文獻[11]給出了控制指令更新算法，本文直接給出最終結論：

(29)

(30)

式中：Rk為正定系數矩陣。

5 MPSP指令修正中制導律設計

本文基于零控交班區域分析并根據MPSP理論方法，對空基臨近空間防御飛行器進行指令修正中制導律設計。

在對質心動力學模型(2)式的求解中，時間作為獨立自變量，因此需要知道中制導全程時間并沿時間正向積分。本文為避免對剩余飛行時間的估計，選取防御飛行器位置坐標x作為動力學模型的獨立自變量。

(31)

對模型(31)式采用歐拉法進行離散化處理：

Xk+1=Fk(Xk,Uk),

(32)

式中：

(33)

由x方向終端位置xd可計算離散步長為

(35)

(36)

式中：yf、γf分別為終端時刻的y方向位置和彈道傾角。

根據(27)式～(30)式可計算更新制導指令：

(37)

6 仿真研究

本節通過仿真比較以檢驗本文所設計的制導律對不同情況的適應性能。采用離散化的非線性動力學模型(32)式進行仿真研究，仿真初始條件及部分參數見表1. 其中，參考坐標系選取與圖1中相同，定義防御飛行器初始位置為坐標原點。

表1 仿真初始參數Tab.1 Initial simulation parameters

根據表1及(16)式和(17)式計算不同末制導彈目速度比下的期望交班位置，計算結果見表2.

表2 不同速度比下的期望交班位置Tab.2 Desired handover locations at different velocity ratios

6.1 制導律性能校驗

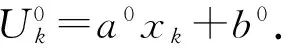
1)a0=-0.2,b0=1，η=1/4；

2)a0=-0.4,b0=1，η=1/4；

3)a0=-0.2,b0=1，η=1/5.

算例的仿真結果分別如圖4～圖6和表3～表5所示。

圖4 算例1多次迭代后的仿真結果Fig.4 Simulated results of Example 1 after multiple iterations

圖6 算例3多次迭代后的仿真結果Fig.6 Simulated results of Example 3 after multiple iterations

表3 算例1終端誤差Tab.3 Terminal errors of Example 1

表4 算例2終端誤差Tab.4 Terminal errors of Example 2

表5 算例3終端誤差Tab.5 Terminal errors of Example 3

比較算例1與算例2可知，在彈目速度比一定的前提條件下，本文設計的制導律對控制初值猜測不敏感。對比表3與表4所得仿真數據，可以看出針對相同的期望交班位置，隨著制導律逐步迭代，制導終端誤差逐漸減小；并且不同的控制指令初值均可使終端誤差在3步后基本收斂。

綜合比較仿真算例1～算例3，初始控制指令都選用自變量的線性形式，針對不同的彈目速度比及控制指令初值，基于MPSP算法設計的中制導律均可保證導彈最終達到期望的中末制導交班位置，并滿足相應的終端角度約束。

6.2 制導律魯棒性校驗

本文通過對初始狀態進行擾動來對所設計制導律的魯棒性進行評估。初始狀態偏差的變化范圍設定為

(38)

在(38)式所確定的初始擾動變化范圍內，采用Monte Carlo方法對制導方法進行效果驗證。分別對不同的初始位置偏差及初始彈道傾角偏差進100次仿真計算，這里Monte Carlo仿真初值選擇與6.1節算例1相同。

由于本文并未對終端速度進行約束，因此不考慮對速度的初始擾動進行仿真。圖7及圖8中曲線表示在初始狀態存在擾動情況下，本文所采用的制導律依舊可以使擾動彈道有效收斂于預期位置，并滿足相應落角約束。

圖7 考慮初始位置誤差的Monte Carlo仿真結果Fig.7 Monte Carlo simulation results in considering the initial location error

圖8 考慮初始角度誤差的Monte Carlo仿真結果Fig.8 Monte Carlo simulation results in considering the initial angle error

7 結論

本文利用零化ZEM思想，對中末制導交班區域進行分析，結論得出了臨近空間防御飛行器中末制導最佳交班位置。應用MPSP理論對考慮交班區域終端約束的指令修正中制導律進行設計。仿真結果表明設計的制導律可以對交班區域進行精準覆蓋，并能滿足位置、角度等終端約束，并且制導律對初始猜測控制指令不敏感。同時，在臨近空間防御飛行器中制導初始狀態受到擾動情況下，設計的中制導律仍舊可以有效完成本文提出的中末制導零控交班任務。

由于制導律控制指令更新為解析形式，并且對于不同仿真情況終端誤差在迭代3次后基本收斂，因此將該制導形式作為修正指令，可較為快速準確地應對臨近空間目標機動，在一定程度上滿足在線制導需求。同時基于MPSP理論的設計方法對在線閉合制導律研究方面同樣具有很大的應用前景。

References)

[1] 黃偉, 羅世彬, 王振國. 臨近空間高超聲速飛行器關鍵技術及展望[J]. 宇航學報, 2010, 31(5):1259-1265. HUANG Wei, LUO Shi-bin, WANG Zhen-guo. Key techniques and prospect of near-space hypersonic vehicle[J]. Journal of Astronautics, 2010, 31(5):1259-1265.(in Chinese)

[2] 呼衛軍, 周軍. 臨近空間飛行器攔截策略與攔截武器能力分析[J]. 現代防御技術, 2012, 40(1):11-15. HU Wei-jun, ZHOU Jun. Analysis of the interception strategy of the near space vehicle and capability of the interception weapon [J]. Modern Defense Technology, 2012, 40(1):11-15. (in Chinese)

[3] Marcel M J, Baker J. Interdisciplinary design of a near space vehicle[C]∥Proceedings of Southeast Conference. Richmond, VA: IEEE, 2007:421-426.

[4] 王還鄉, 李為民, 上官強, 等. 高超聲速飛行器巡航段攔截作戰需求分析[J]. 戰術導彈技術, 2012(2): 36-40． WANG Huan-xiang, LI Wei-min, SHANGGUAN Qiang, et al. Analysis of the battle demand to interception on the cruise phase of hypersonic vehicle[J]. Tactical Missile Technology, 2012(2):36-40.(in Chinese)

[5] 熊俊輝, 唐勝景, 郭杰. 基于空基攔截器的高超聲速飛行器防御攔截[J]. 現代防御技術, 2014, 42(1): 14-18. XIONG Jun-hui, TANG Shen-jing, GUO Jie. Defense strategy of hypersonic vehicle based on air launched interceptor [J]. Modern Defense Technology, 2014, 42(1): 14-18. (in Chinese)

[6] 梁海燕. 反臨近空間高超聲速飛行器導引頭及關鍵技術分析[J]. 飛航導彈, 2013(3): 61-63． LIANG Hai-yan. The key technology of seekers for anti-hypersonic vehicle in the near space[J]. Winged Missiles Journal, 2013(3): 61-63. (in Chinese)

[7] 趙杰, 王君, 張大元,等. 反臨近空間高超聲速飛行器中末交接視角研究[J]. 飛行力學, 2015, 33(3):253-256. ZHAO Jie, WANG Jun, ZHANG Da-yuan, et al. Visual angle research for midcourse and terminal guidance hand-over of near space hypersonic vehicles[J]. Flight Dynamics, 2015, 33(3):253-256. (in Chinese)

[8] 樊會濤. 復合制導空空導彈截獲目標概率研究[J]. 航空學報, 2010, 31(6):1225-1229. FAN Hui-tao. Study on target acquisition probability of air-to-air missiles with combined guidance [J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(6):1225-1229. (in Chinese)

[9] 李洪鈳, 張斌, 趙雨. 采用雙機協同的指令修正慣性中制導方法[J]. 空軍工程大學學報：自然科學版, 2016, 17(1):13-18. LI Hong-ke, ZHANG Bin, ZHAO Yu. A study of method of command amendment inertial midcourse guidance based on dual aircraft cooperation[J]. Journal of Air Force Engineering University: Nature Science Edition, 2016, 17(1):13-18.(in Chinese)

[10] 姚郁, 鄭天宇, 賀風華,等. 飛行器末制導中的幾個熱點問題與挑戰[J]. 航空學報, 2015, 36(8):2696-2716. YAO Yu, ZHENG Tian-yu, HE Feng-hua, et al. Several hot issues and challenges in terminal guidance of flight vehicles [J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(8):2696-2716. (in Chinese)

[11] Ryu M Y, Lee C H, Tahk M J. Command shaping optimal guidance laws against high-speed incoming targets [J]. Journal of Guidance, Control, and Dynamics, 2015, 38(10): 1-8.

[12] Dou L, Dou J. Design of optimal guidance laws with multi-constraints considering time-varying parameters[J]. Transactions of the Japan Society for Aeronautical & Space Sciences, 2013, 56(6):323-327.

[13] Padhi R, Kothari M. Model predictive static programming: a computationally efficient technique for suboptimal control design[J]. International Journal of Innovative Computing Information and Control, 2009, 5(2):399-411.

[14] Halbe O, Raja R G, Padhi R. Robust reentry guidance of a reusable launch vehicle using model predictive static programming[J]. Journal of Guidance Control & Dynamics, 2014, 37(1):134-148.

[15] Dwivedi P N, Bhattacharya A, Padhi R. Suboptimal midcourse guidance of interceptors for high-speed targets with alignment angle constraint[J]. Journal of Guidance Control & Dynamics, 2011, 34(3):860-877.

[16] Oza H B, Padhi R. Impact-angle-constrained suboptimal model predictive static programming guidance of air-to-ground missiles[J]. Journal of Guidance Control & Dynamics, 2012, 35(1):153-164.

[17] Newman B. Exoatmospheric intercepts using zero effort miss steering for midcourse guidance[C]∥Proceedings of AAS/AIAA Spaceflight Mechanics Meeting. Passadena, CA, US: AIAA, 1993: 415-433.

[18] Newman B. Spacecraft intercept guidance using zero effort miss steering, AIAA 93-3890[R]. Reston, VA, US: AIAA, 1993:1707-1716.

[19] 鄭立偉, 荊武興. 大氣層外攔截器近最優中制導律設計[J]. 宇航學報, 2008, 29(1):235-241. ZHENG Li-wei, JING Wu-xing. Design of a near optimal midcourse guidance law for exoatmospheric interceptor [J]. Journal of Astronautics, 2008, 29(1):235-241. (in Chinese)

[20] Zarchan P. Tactical and strategic missile guidance [M]. 6th ed. Reston, VA, US: American Institute of Aeronautics & Astronautics, 1990.

Research on Command Correction Midcourse Guidance Law with Zero Effort Handover in Near Space

ZHANG Hao-qiang1， TANG Sheng-jing1， GUO Jie1， LIU Xiao1， XU Qian2

(1.Key Laboratory of Dynamic and Control of Flight Vehicle of the Ministry of Education, School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China;2.Beijing Institute of Aerospace System Engineering, Beijing 100076, China)

A space-based cruise phase defense strategy is proposed for near-space hypersonic vehicles. Considering the properties of near-space defense, a valid zero effort interception handover (ZEH) region and its performance criterions are presented by analyzing the handover region, which connects the midcourse and terminal guidance phases. Based on the model predictive static programming (MPSP) theory and the terminal constraints of midcourse phase, a close-formed solution is derived as the command correction guidance law. The proposed guidance law is used for simulation. The simulated results show that a small velocity-ratio condition for terminal engagement is satisfied by ZEH. The proposed method can improve the computational efficiency significantly, and also meet the requirement of ZEH constraint. A large number of Monte Carlo simulations show the robustness of the guidance law against initial disturbances.

ordnance science and technology; flight vehicle design; zero effort miss distance; handover point; model predictive static programming; midcourse guidance

2016-05-04

國家自然科學基金項目(11572036)

張浩強(1989—)，男，博士研究生。E-mail:724158160@qq.com

唐勝景(1959—)，男，教授，博士生導師。E-mail:tangsj@bit.edu.cn

TJ765.3+31

A

1000-1093(2017)03-0483-11

10.3969/j.issn.1000-1093.2017.03.010