基于凸優化的水下載體定位研究

曹俊， 鄭翠娥， 孫大軍， 張殿倫

(1.哈爾濱工程大學 水聲工程學院, 黑龍江 哈爾濱 150001; 2.哈爾濱工程大學 水聲技術重點實驗室, 黑龍江 哈爾濱 150001)

基于凸優化的水下載體定位研究

曹俊1,2， 鄭翠娥1,2， 孫大軍1,2， 張殿倫1,2

(1.哈爾濱工程大學 水聲工程學院, 黑龍江 哈爾濱 150001; 2.哈爾濱工程大學 水聲技術重點實驗室, 黑龍江 哈爾濱 150001)

基于單信標測距的定位方法，是水聲定位技術一個新的研究方向，具有重要應用價值。針對單信標測距定位問題最小二乘結構，對高度非凸的測距定位方程首次提出了基于凸優化的解算方法。對帶有誤差的測距量測方程添加不等式約束條件，將其改寫為有約束的解算方程；對目標函數和約束條件進行放射近似，將其進行凸化處理；引入松弛變量和罰函數，降低對迭代初值的敏感度。仿真結果表明：對于不同量級的初值誤差，定位結果的差別在厘米量級，所提算法不需要可靠的初值即能迭代收斂得到高精度的定位結果；信標與圓形航跡的圓心距離越近，定位精度越高。通過湖上試驗，進一步驗證了所提算法的有效性。

信息處理技術； 單信標測距； 虛擬信標； 凸優化； 約束條件； 罰函數

0 引言

隨著海洋開發活動進程的加快，水下載體定位的重要性越來越強。基于單信標距離測量的定位方式只需要一個海底聲信標，占用資源少，具有重要的應用價值[1-4]，最近吸引了越來越多專家學者的研究興趣。基于單信標距離測量的定位解算方法中，文獻[5]最早提出使用最小二乘法解算出無人水下潛航器(UUV)的水平初始位置，通過直接降階的方式將定位方程兩兩相減消除二次項，構成線性方程組，從而實現對UUV位置的求解。文獻[6]通過松弛最小二乘模型為半定規劃問題，但是經過這樣處理的定位方案在最小二乘意義上不再是最優估計。文獻[7]提出了基于距離平方的最小二乘定位方案，但這個方法只是近似最大似然估計，所以得到的定位結果仍然是次優的。基于最小二乘法的定位方法是一種重要的解決方案，它不僅能夠提供低復雜度的解決過程，還能夠得到可靠的定位估計精度。眾所周知，最小二乘法是凸優化問題的一種特殊形式，盡管關于最小二乘問題的求解技術已經有比較成熟的技術，但是帶有測量誤差的最小二乘測距定位方程是高度非凸的。如果能將非凸定位方程函數凸化，轉化成凸優化的問題，就能有效地進行求解[8]。

本文針對單信標測距定位問題，首次針對定位問題中的最小二乘結構提出了基于凸優化的解算方法。首先，根據最小二乘理論推導出定位解算的目標函數，將目標函數經過公式推導和形式轉換，使之與凸優化理論中的凸差(DC)結構形式相符合，并根據測距誤差情況添加約束條件。DC結構問題可以利用凹凸處理(CCP)算法，通過目標函數凸化將DC問題轉化成凸優化問題求解，進而達到利用凸優化的方法解決定位方程的目的。其次，針對CCP算法對初值要求比較高(初值必須在可行域內)的缺點，引入序列無約束極小化的罰函數，放寬對初始點要求的優點，引入罰函數，放寬CCP算法對初值的要求，增強算法的適應性。最后，對提出的基于凸優化理論的定位解算方法進行了仿真分析和湖試數據分析，進一步驗證了所提算法的有效性。

1 基于凸優化的單信標測距定位原理

單信標測距定位系統主要由海底聲信標和安裝在水下載體上的測距儀組成。海底聲信標的位置事先標定得到，利用聲信號傳播的往返時間可以確定被定位載體與海底聲信標之間的距離[9-10]。原理上，單次距離測量不能確定水下載體的具體位置，所以需要結合水下載體工作時的運動參數如速度和姿態來實時解算出水下載體的位置，如圖1所示。其中VT1、VT2直到VTn-1不是真實存在的，它們是根據水下載體兩個測距周期之間的載體位移虛擬出來的，故也可稱之為虛擬信標。例如Xb(n-1)至Xbn的位移為ΔXb(n-1),bn=vb(n-1),bnT，則虛擬信標VTn-1的位置為VTn+ΔXb(n-1),bn，v為大地坐標系下的水下載體運動速度，T為測距周期。解算第n個測量點需要利用測量點1～n的測距信息和載體運動參數，解算第n+1個測量點需要利用測量點2～n+1的測距信息和載體運動參數，依此類推基于單信標測距完成對水下載體的跟蹤定位[11]。

圖1 單信標測距定位原理Fig.1 Single beacon ranging and positioning principle

定位方程中，水下載體與信標之間存在噪聲干擾，則第i個測量點對應的距離測量方程滿足

ri=‖x-xti‖+εi,i=1,2,…,n，

(1)

式中：虛擬信標VTi的坐標為xti；水下載體要定位的位置Xbn的坐標為x；ri為水下載體與第i個虛擬信標之間的距離；εi表示水下載體與第i個虛擬信標進行距離測量時存在的未知噪聲干擾，該未知噪聲干擾由測時誤差和聲速誤差共同決定。

單信標測距定位問題最初的形式是一個非凸的優化問題，可以描述為根據有噪聲干擾的測距信息估計水下載體位置的問題，定位問題就是基于距離的最小二乘估計問題：

(2)

為了對定位問題進行分析，本文首先介紹DC問題的標準形式：

(3)

式中：x∈Rn，并且fi和gi都是凸函數。

在CCP優化過程中，通過將DC問題中的gi(i=0,…,n)仿射近似，可以利用迭代方法進行最優值求解。轉化后的形式為

(4)

式中：xk為第k次迭代時的水下載體位置迭代量。

首先找到一個可行域內的初值x0，通過迭代過程，求解CCP結構方程，從而得到DC問題的最優解。

根據DC問題和CCP優化的定義，本文對單標定位最小二乘估計的目標函數展開去除常數項后得到

(5)

對展開后的目標函數，對照DC結構的標準形式有如下定義：

(6)

則目標函數可以表示為F(x)=f(x)-g(x)的形式，因為其中的f(x)和g(x)都是凸函數，所以目標函數滿足DC結構的形式。

g(x)在xk處的估計值可以表示為

(7)

得到目標函數的凸化之后的形式為

(8)

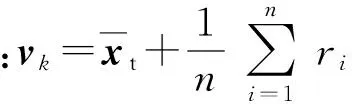
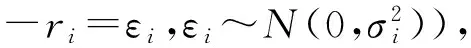
(9)

不等式展開后形成兩個新的不等式，‖xk-xti‖-ri-δi≤0和ri-δi≤‖xk-xti‖.

第1個不等式的fi(x)=‖xk-xti‖-ri-δi，gi(x)=0，滿足凸優化的約束條件fi(x)-gi(x)≤0；第2個不等式的fi(x)=ri-δi，gi(x)=‖xk-xti‖. 對gi(x)=‖xk-xti‖在xk處進行線性化處理得到i(x,xk)=‖xk-xti‖+?‖xk-xti‖T(x-xk)，則第2個不等式可以寫為-‖xk-xti‖-?‖xk-xti‖T(x-xk)+ri-δi≤0，滿足于凸優化的約束條件fi(x)-i(x,xk)≤0. 所以，第k次迭代的時候，凸優化問題可以描述為

(10)

CCP算法中要求初值必須是可行域內的值，為了降低初值的限制，引入非負的松弛變量si≥0和i≥0，用它們來代替約束條件右側的0來提升上界，這就形成了新的有約束條件的凸優化問題：

(11)

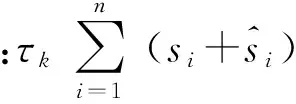
若xk是可行域內的值，則松弛變量滿足si=0和i=0，且新的凸優化問題與原來的凸優化問題是一樣的。若xk不是可行域內的值，則松弛變量滿足si>0和i>0，且0，新的凸優化問題與原來的凸優化問題相比多了).之所以被稱為懲罰項，是因為隨著迭代次數的增加，τk不是一個確定的參數，而是遞增的，這便具有了懲罰的含意。當xk不是可行域內值的時候，目標函數被逐漸增大，求極小值又期望將xk拉回到可行域內，最終xk會被拉到不可行域和可行域的邊界處，松弛變量si和i也會相應地減小直至為0，進而在可行域內求得xk的最優解。所以，松弛變量si和i的引入會放寬初值限制，在約束條件中引入單調遞增的懲罰因子τk，算法的松弛變量能夠減小得更快，當松弛變量減小到特別小的時候，迭代過程能很快變得可行。

綜上分析，本文提出的基于凸優化單信標測距定位算法詳細流程如表1所示。

表1 基于凸優化的定位算法流程Tab.1 Positioning algorithm based on convex optimization

表1中，測距誤差邊界δ的值選擇為信標測距精度的3倍；初始罰因子τ0=1；懲罰因子增長因子μ在5～10之間選擇；迭代次數最大值選擇為50次。

綜上分析，只要是基于信標測距的定位導航系統，都能夠使用本文提出的基于凸優化的解算方法。并且本文算法具有兩方面優點：一方面，對于存在噪聲干擾的測距量測量，根據統計得到的測距精度對測距方程添加測距誤差邊界條件；另一方面，當不知道載體比較準確的初始位置時，也能夠迭代解算得到載體位置，放寬了對初始位置的要求。

2 計算機仿真分析

本節中，在Matlab環境中對基于凸優化的單信標測距定位算法進行仿真分析，驗證所提出的算法的有效性，并對相關仿真結果進行分析。仿真參數為：海底布放的單只聲信標的坐標為AT=(0 m,0 m,100 m)。水下載體在恒定深度為100 m的深度作環形機動，前向運動速度恒定為1 m/s. 對布放的單只信標的測距周期為10 s. 添加呈高斯分布的隨機測距誤差N=(0 m,1.52m)。水下載體按圓形航跡機動完成后，根據測距信息和虛擬信標的位置實現對水下載體終點位置的定位。

為了分析本文算法對定位精度的提高，將本文算法與最小二乘法進行比對。接收信標信號的信噪比高的時候，相應的測距誤差小；接收信標信號的信噪比低的時候，相應的測距誤差大。本文算法與最小二乘法的對比見表2，采用蒙特卡洛法進行1 000次實驗。從表2中可知，對于不同量級的測距誤差，本文算法的定位精度都高于最小二乘法的定位精度；測距誤差越大，本文算法對定位精度的提高與最小二乘法定位精度的比值越高。

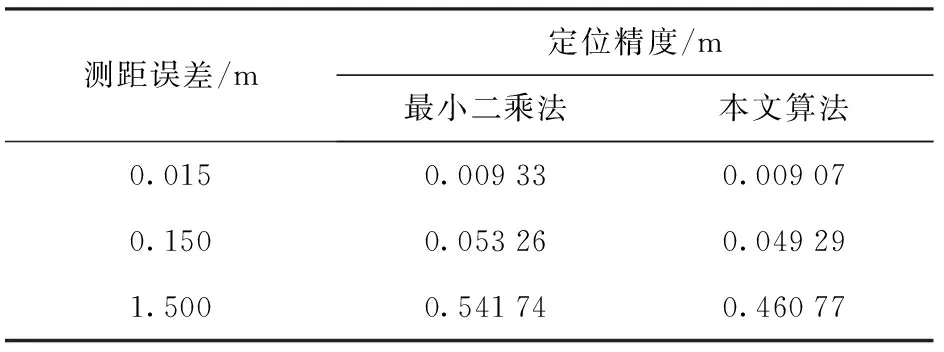
表2 本文算法與最小二乘法對比Tab.2 Comparison between the algorithm proposed in this paper and the least square method

為了驗證迭代初值對定位結果的影響，對水下載體的迭代初值添加幾十米量級和幾百米量級的初值誤差。圖2為使用本文提出的算法得到的圓形航跡終點的定位結果。圖2(a)對水下載體的迭代初值添加東向20 m和北向30 m的初值誤差，本文算法對圓形航跡終點定位結果的根均方誤差為0.684 55 m. 圖2(b)對水下載體的迭代初值添加東向200 m和北向300 m的初值誤差，本文算法對圓形航跡終點定位結果的根均方誤差為0.664 52 m. 對于航位推算的定位結果，在不存在其他誤差的情況下，定位誤差的大小與初始位置誤差大小相同。比對兩幅圖可以看出，對于不同量級的初值誤差，定位結果的根均方誤差的差別在厘米量級，本文算法不需要可靠的初值即能迭代收斂得到高精度的定位結果。

圖2 迭代初值誤差對定位結果影響Fig.2 Influence of iterative initial value error on positioning results

為了驗證信標位置與圓形航跡圓心距離對定位結果的影響，信標與圓形航跡圓心分別相距0 m和35 m. 圖3為使用本文提出的算法得到的圓形航跡終點的定位結果。圖3(a)信標與圓形航跡圓心相距0 m，本文算法對圓形航跡終點定位結果的根均方誤差為0.383 21 m. 圖3(b)信標與圓形航跡圓心相距35 m，本文算法對圓形航跡終點定位結果的根均方誤差為0.421 86 m. 圖2(a)信標與圓形航跡圓心相距70 m. 比對圖3(a)、圖3(b)和圖2(a)可以看出，信標與圓形航跡的圓心距離越近，定位精度越高。

圖3 信標位置與圓心距離對定位結果影響Fig.3 Influence of distance between beacon and center on the positioning results

3 湖試數據分析

2015年9月在某湖面進行了單信標測距定位的外場湖試試驗。試驗地點的水深約為43 m. 試驗平臺為小型旅游船。水面試驗設備包括：法國IXBLUE公司的RAMSES6000聲學測距系統，測距系統的時延測量精度能達到100 μs的水平，測距系統為分體式結構。法國IXBLUE公司的Octans高精度羅經，航向角可以保持0.1°正切維度的動態精度，分辨率0.01°；橫滾角和俯仰角可以保持0.01°的動態精度，分辨率0.001°. 美國RDI公司的聲學多普勒測速儀ADCP/DVL，600 kHz工作主頻的情況下作用高程為0.7～90 m，載體航行速度v的情況下，測量的對水底速度的精度大概為±3‰·v±0.002 m/s. 瑞士Leica公司的Leica 1200型差分全球定位系統(GPS) ，在RTK模式下工作時對低速運動目標的定位精度能夠達到2～3 cm.

水面試驗設備安裝示意圖如圖4所示。羅經固定于試驗船船艙內，偏航方向正對試驗船船艏。多普勒測速儀通過三腳架固定安裝在試驗船右舷后側，相對于羅經向下0.47 m. GPS天線安裝在三腳架頂端，相對于羅經向上2.87 m. 聲學測距系統的分體式換能器頭通過鋼管固定安裝在試驗船左舷后側，相對于羅經向下2.78 m.

圖4 水面試驗設備安裝示意圖Fig.4 Schematic diagram of surface test equipment installation

水下試驗設備為法國IXBLUE公司的RTA系列聲信標，聲信標的時延測量精度能達到100 μs的水平，聲信標為一體式結構，如圖5(a)所示。聲信標通過錨系結構布放于湖底，錨系結構如圖5(b)所示。聲信標的釋放機構朝下，釋放機構卡住O型釋放環，釋放環通過軟繩與沉塊相連，繩長5 m；聲信標的換能器頭朝上，通過軟繩與浮球相連，繩長5 m，浮球提供的浮力使聲信標能夠盡量保持垂直狀態。水面接一浮球，用于標識聲信標的大概位置，便于水面試驗船圍繞聲信標走航跡。

圖5 聲信標及錨系結構Fig.5 Acoustic beacon and anchor system structure

試驗中，水面試驗船在水面浮球外側作環形機動，半徑大概為35 m. 聲學測距系統對聲信標的測距周期為5 s. 迭代初值添加東向20 m和北向30 m的初值誤差。將終點處的定位結果與GPS真值進行比較來評價定位精度。圖6為使用本文提出的算法得到的圓形航跡終點的定位結果。圖6(a)信標在圓形航跡外側，本文算法對圓形航跡終點定位結果的根均方誤差為4.382 3 m. 圖6(b)信標在圓形航跡內側，本文算法對圓形航跡終點定位結果的根均方誤差為2.676 5 m. 比對兩幅圖可以看出，信標在圓形航跡內側的定位精度高于信標在圓形航跡外側的定位精度，這與仿真分析的結論一致。

圖6 湖試結果Fig.6 Lake trial results

4 結論

針對水下載體的單信標測距定位研究，本文提出了一種基于凸優化的單信標測距定位解算方法：1)對高度非凸的測距定位方程進行凸優化處理，得到凸的目標函數，得到全局最優解；2)考慮測距系統由于噪聲干擾存在的測距誤差，添加不等式約束條件；3)引入罰函數，降低對迭代初值的敏感度。

對提出的定位解算方法進行仿真分析，仿真結果表明：1)對于不同量級的初值誤差，定位結果的根均方誤差的差別在厘米量級，本文算法不需要可靠的初值即能迭代收斂得到高精度的定位結果；2)信標位置與圓形航跡圓心距離不同時，定位結果的根均方誤差的差別在分米量級，信標與圓形航跡的圓心距離越近，定位精度越高。

通過湖上試驗，進一步驗證了本文所提算法的有效性。

References)

[1] Gaurav C, Arpita S, Twinkle T, et al. Conditions for target tracking with range-only information[J]. Robotics and Autonomous Systems, 2016, 75: 176-186.

[2] 孫大軍, 鄭翠娥. 水聲導航、定位技術發展趨勢探討[J]. 海洋技術學報, 2015,34(3): 64-65. SUN Da-jun, ZHENG Cui-e. Discussion on development trend of underwater acoustic navigation and positioning technology[J]. Journal of Ocean Technology, 2015,34(3): 64-65. (in Chinese)

[3] 郭雅靜, 李春雨, 張東升, 等. 基于航位推算/水聲定位系統的水下拖體組合導航方法[J]. 海洋地質前沿, 2015, 31(6): 63-67. GUO Ya-jing, LI Chun-yu, ZHANG Dong-sheng,et al. The integrated navigation method by underwater towing body based on dead reckoning/hydroacoustic positioning system[J]. Marine Geology Frontiers, 2015, 31(6): 63-67. (in Chinese)

[4] Hegrenas O, Gade K, Hagen O K, et al. Underwater transponder positioning and navigation of autonomous underwater vehicles[C]∥MTS/IEEE Biloxi-Marine Technology for Our Future: Global and Local Challenges. Biloxi, MS, US: MTS, 2009.

[5] Alexander P S. The AUV positioning using ranges from one transponder LBL [C]∥Proceedings of the 1995 MTS/IEEE Oceans Conference. San Diego, CA, US: MTS,1995:1620-1623.

[6] Vandenberghe L, Boyd S. Semidefinite programming[J]. SIAM Review, 1996,38(1): 40-45.

[7] Beck A, Stoica P, Li J. Exact and approximate solutions of source localization problems[J]. IEEE Transactions on Signal Processing, 2008,56(5): 1770-1778.

[8] Yuille A L, Rangarajan A. The concave-convex procedure[J]. Neural Computation, 2003, 15(4): 915-936.

[9] 劉明雍, 李聞白, 劉富檣, 等. 基于單信標測距的水下導航系統可觀測性分析[J]. 西北工業大學學報, 2011, 29(1): 87-92. LIU Ming-yong, LI Wen-bai, LIU Fu-qiang, et al. Observability analysis of underwater navigation system based on single beacon ranging [J]. Journal of Northwestern Polytechnical University, 2011, 29(1): 87-92. (in Chinese)

[10] 嚴衛生, 房新鵬, 崔榮鑫. 單信標測距AUV水下定位系統觀測性分析[J]. 中南大學學報:自然科學版, 2012, 43(8): 3085-3090. YAN Wei-sheng, FANG Xin-peng, CUI Rong-xin. Observability analysis of single-beacon underwater localization of autonomous underwater vehicle [J]. Journal of Central South University:Natural Science Edition, 2012,43(8): 3085-3090. (in Chinese)

[11] Baccou P, Jouvencel B. Homing and navigation using one transponder for AUV, post-processing comparisons results with long base-line navigation [C]∥IEEE International Conference on Robotics and Automation.Washington, DC, US: IEEE,2002.

Research on the Positioning of Underwater Vehicle Based on Convex Optimization

CAO Jun1,2， ZHENG Cui-e1,2， SUN Da-jun1,2， ZHANG Dian-lun1,2

(1.College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, Heilongjiang, China;2.Acoustic Science and Technology Laboratory, Harbin Engineering University, Harbin 150001, Heilongjiang, China)

The localization method based on single beacon ranging is a new research direction of underwater acoustic positioning technology. A method based on convex optimization is proposed for the first time to solve the least square structure for the single beacon ranging and locating. An inequality constraint condition is added to the ranging equation with errors, and the ranging equation is reformulated as a constrained solution equation. The objective function and constraint condition are approximated by radiation, and the convex processing is carried out. The slack variable and penalty function are introduced to reduce the sensitivity of iteration initial value. Simulated results show that the difference of positioning results is in centimeter order of magnitude for different magnitudes of initial errors. The proposed algorithm can be iterated convergence to get high accuracy of the positioning results without reliable initial value. When the beacon is close the center distance of circular track, the positioning accuracy is higher. The effectiveness of the proposed algorithm is verified by experiments on the lake.

information processing technology; single beacon ranging; virtual beacon; convex optimization; constraint condition; penalty function

2016-07-04

國家自然科學基金項目(61531012)；國家國防科技工業局技術基礎科研項目(B2420133002)

曹俊(1987—), 男, 博士研究生。E-mail: caojun1105@sina.cn

張殿倫(1967—), 男, 教授, 博士生導師。E-mail: zhangdianlun@hrbeu.edu.cn

TB568

A

1000-1093(2017)03-0520-07

10.3969/j.issn.1000-1093.2017.03.014