基于快速拋光技術的光學元件材料去除模型研究

林濤, 楊煒, 王健

(1.廈門大學 航空航天學院， 福建 廈門 361005; 2.中國工程物理研究院 激光聚變研究中心， 四川 綿陽 621900)

基于快速拋光技術的光學元件材料去除模型研究

林濤1, 楊煒1, 王健2

(1.廈門大學 航空航天學院， 福建 廈門 361005; 2.中國工程物理研究院 激光聚變研究中心， 四川 綿陽 621900)

為精確控制拋光階段材料去除，實現光學元件的確定性拋光加工，在分析快速拋光原理和快速拋光材料去除機制基礎上，從單顆磨粒受力和拋光墊峰點捕獲的磨粒數出發，獲得量化的單顆磨粒瞬時切除體積和拋光接觸區參與有效磨粒數，從而建立一種光學元件快速拋光材料去除模型。研究結果表明：以材料去除量為實驗對象，在不同拋光液、拋光墊和光學元件實驗條件下，材料去除模型的理論預測結果與實驗結果較為吻合,材料去除量誤差可以控制在9%以內。驗證了該模型對于光學元件快速拋光技術的適用性，從而可以確定性的控制快速拋光時間和效率。

機械制造工藝與設備； 光學元件； 快速拋光； 材料去除模型

0 引言

針對激光核聚變研究，我國相關部門已建成神光Ⅰ、神光Ⅱ高功率激光裝置，現在進行的神光Ⅲ裝置的建設和研究更是一項龐大而又復雜的巨型工程，其中使用了大量的光學元件，光學元件超精密加工表面質量控制問題已經成為慣性約束聚變研究中重點關注的問題，直接影響著強激光系統的使用性能[1-3]。目前，我國高精密光學元件加工水平和世界上技術先進國家相比還有一定的差距，提高光學元件高效批量化加工，是擺在我國光學制造領域的一個重要課題。

傳統平面光學元件在拋光加工過程中，需要經過粗拋、環形拋光和精拋才能提高元件表面面型精度，降低表面粗糙度和亞表面缺陷[4]，整個拋光流程耗時長，不能滿足大型光學工程的需求。快速拋光技術以其相對較高的材料去除率，已經全面取代了初拋，部分取代了環形拋光。因此，研究快速拋光技術的材料去除機制和模型，實現確定性的拋光技術尤為重要。

國內外學者對拋光技術的材料去除機制已經開展了廣泛的研究，近年來也提出了一些相應的材料去除模型。例如：Luo等[5]基于磨粒磨損機制，針對硅片化學機械拋光(CMP)提出了材料微觀去除模型，并建立了材料去除公式；Runnels等[6]提出了流體潤滑模型，采用流體動力學方程建立了芯片表面拋光液流動模型；Christopher等[7]基于化學作用機制，應用化學動力學理論，提出拋光過程中的五步去除機制；Zhao等[8]基于原子/分子去除機制，認為拋光是表面的最外層原子或分子不斷氧化和磨損的動態平衡過程。目前材料去除機理和去除模型的研究非常多而深入，幾乎沒有一個模型具有普遍適用性，但不同的運用場合可以有改進和補充的空間。

本文從磨粒磨損機制出發，建立一種光學元件快速拋光材料去除模型，驗證了在不同類型光學元件、不同類型拋光墊和不同類型拋光液條件下，模型能夠適應光學元件的快速拋光，實現確定性拋光技術，材料去除誤差可以控制在合理的范圍之內。

1 光學元件快速拋光技術

1.1 快速拋光原理及材料去除機制

快速拋光原理如圖1所示，將光學元件置于運動控制軸下端，將拋光墊貼在旋轉拋光盤上；元件在運動控制軸的控制下可以獨立旋轉，運動控制軸可以上下移動，以此對元件施加不同的壓力；拋光液通過噴管噴射到拋光墊表面，并通過拋光盤的旋轉均勻散布到元件和拋光墊表面；元件相對于拋光墊運動，在機械磨削與化學侵蝕兩種材料去除機制的交互作用下完成快速拋光加工。傳統環形拋光只是靠元件重力，且元件是被動運動，快速拋光與初拋和環形拋光的區別之處在于有了加壓裝置，而且元件是主動運動，元件具有運動的獨立性和快速性，且外界可對元件施加較大的壓力[9]。

圖1 快速拋光原理Fig.1 Fast polishing principle

對于快速拋光材料去除機制的研究首先要關注光學元件和拋光墊的接觸狀態。在拋光加工過程中，根據拋光盤和元件的接觸狀態及拋光液的潤滑狀態，元件和拋光盤之間的接觸狀態主要有3種：完全接觸狀態、部分接觸狀態、不接觸狀態 (流體潤滑狀態)。根據上述3種接觸狀態，可以將材料去除機理主要擴展為4種：磨粒磨損機制、流體潤滑機制、原子/分子去除機制和化學作用機制。光學元件快速拋光技術一個顯著特點就是擁有較高的材料去除率，其是基于較大的加工壓力和較大的相對速度來實現的，光學元件和拋光墊的接觸屬于完全接觸[10-11]。據此，快速拋光與CMP不同之處在于CMP更多考慮了化學因素，而在光學元件的快速拋光過程中，基于磨粒磨損機制的機械磨削作用在材料去除中占據主導地位，流體潤滑和化學作用相對較小。

1.2 快速拋光材料去除模型

Luo等[5]基于磨粒磨損機制，認為元件和拋光墊直接接觸且達到穩定接觸狀態，并進一步研究元件和拋光墊的實際接觸面積、單顆參與去除材料有效磨粒受力、材料去除的有效磨粒數和單顆有效磨粒切除體積等因素，提出建立拋光材料去除模型所需3個前提條件：規律性分布的拋光墊表面峰點，拋光顆粒粒度正態分布，拋光顆粒、元件、拋光墊之間的塑性形變。通過對這3個前提條件驗證，從而建立拋光材料去除模型[5,12]：

(1)

式中：MRR是材料去除量；ρw是元件的密度；ΔV是單顆有效磨粒瞬時切除體積；N是接觸區內有效磨粒數；xavg,a是接觸區有效磨粒的平均粒徑；F是單顆有效磨粒的受力；Hw是元件的硬度；v是元件相對于拋光墊的相對速度；n是拋光墊峰點捕獲的磨粒數；Φ(z)是正態分布函數。

基于磨粒磨損機制的材料去除模型不足之處在于：1)忽略了填充在拋光墊中的磨粒數與拋光墊材質的軟硬條件有關，在其他加工條件不變的情況下，填充在軟質拋光墊的磨粒數明顯要高于填充在硬質拋光墊的磨粒數[13]；2)忽略了接觸區拋光墊峰點捕獲的磨粒數與外界下壓壓力有關，當壓力較大時，拋光墊峰點接觸面積增大，捕獲的磨粒數也相應增加。這兩點不足導致了材料去除模型在建立過程中，一些假設條件的考慮出現了不完整性，從而導致了單顆有效磨粒的受力、參與磨削的有效磨粒數等因素計算出現了偏差。

針對以上的不足，從兩個方面對材料去除模型進行改進：單顆有效磨粒的受力、接觸區拋光墊峰點捕獲的磨粒數。從磨粒填充角度出發，引入磨粒的拋光墊表面填充因子kc，則單顆有效磨粒的受力F[14-15]可表示為

(2)

式中：p是接觸區的壓力。

根據彈性力學接觸模型[5,16]可得

(3)

(4)

根據元件在加工中處于動態的平衡可得接觸區壓力為

(5)

圖2是拋光顆粒嵌入拋光墊和劃擦元件的放大示意圖，hw為拋光顆粒嵌入元件的深度，hp為拋光顆粒嵌入拋光墊的深度，2xw為拋光顆粒同元件接觸區域的直徑，2xp為拋光顆粒同拋光墊接觸區域的直徑。根據維氏硬度計算公式，

(6)

式中：Hp是拋光墊的硬度。

圖2 單顆有效拋光顆粒嵌入拋光墊和劃擦元件示意圖Fig.2 Model of single effective polishing particles embedded in polishing pad and element

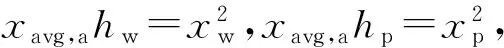
(7)

根據(6)式和(7)式，可以計算出單顆有效磨粒對元件表面的瞬時切除體積,如圖3所示。

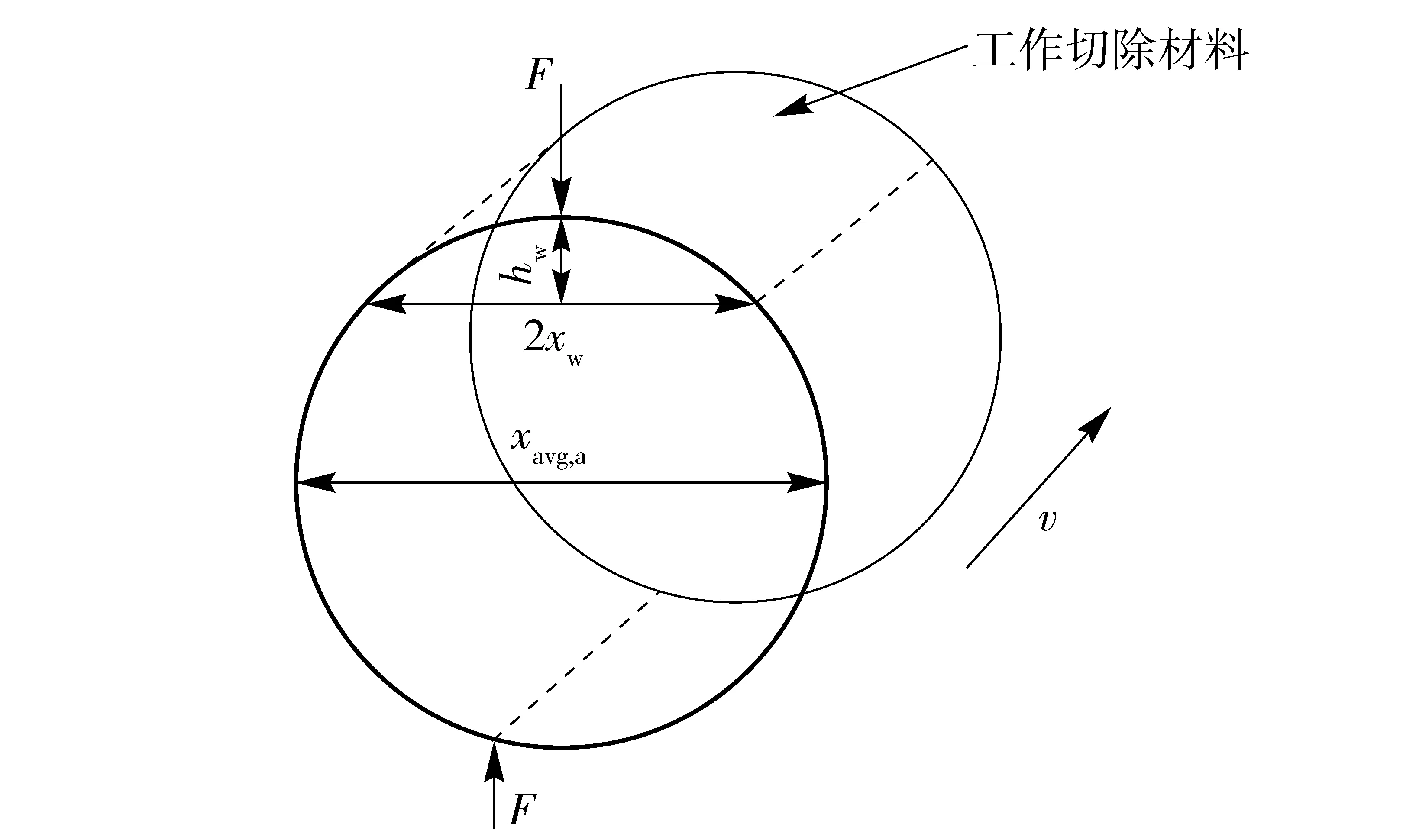
圖3 單顆有效拋光顆粒瞬時切除元件材料示意圖Fig.3 Model of material removed by single effective polishing particles

因此，單顆有效磨粒瞬時切除體積ΔV，

(8)

可以看出：單顆磨粒瞬時切除體積隨著拋光磨粒的粒徑，拋光墊彈性模量，外界所施加的壓力，以及相對速度的變大而變大；單顆磨粒瞬時切除體積隨著元件硬度的變小而變大。

在3個假設條件下：磨粒均勻分布在拋光液中；所有的拋光顆粒在外形上是球形的，且直徑為xavg，a；鑲嵌在拋光墊上的磨粒密度和在拋光液中的密度一致，計算出拋光墊峰點捕獲的磨粒數n為

(9)

式中：q是面密度；χ是體積密度；Ca是拋光液中磨粒的質量分數；ρf是拋光液的密度；ρs是磨粒的密度。

當元件受到外界壓力后，首先和拋光墊接觸，拋光墊峰點產生彈性形變，最先嵌入拋光墊峰點的是粒徑最大的磨粒(粒徑為xmax)，hmax是最大磨粒嵌入元件深度和嵌入拋光墊深度之和，在元件和拋光墊之間存在一個由最大粒徑磨粒產生的間隔g=xmax-hmax. 隨著接觸狀態向穩態接觸過度，粒徑大于g的拋光顆粒開始逐漸嵌入到拋光墊中，由于元件和拋光墊有強烈的直接接觸趨勢，而且拋光顆粒傾向于緊密排列，最終達到穩態接觸狀態。在這個過程中，間隔g始終保持不變，元件和拋光墊接觸區去除元件材料的有效磨粒就是粒徑大于間隔g的磨粒。

拋光顆粒粒徑分布符合正態分布，概率密度函數為

(10)

式中：xavg為拋光顆粒的平均粒徑；σ是粒徑的標準偏差。

由此可得粒徑正態分布函數Q(x)為

(11)

由正態分布的性質和快速拋光中有效磨粒的定義可得，接觸區內有效磨粒數N為

(12)

(13)

有效磨粒的平均尺寸隨著正向壓力的變化而變化。但是,當標準偏差σ很小時,有效磨粒平均尺寸隨著正向壓力的改變很小。因此,有效磨粒的平均尺寸xavg,a可以認為是恒量kxavg.

將(9)式代入(12)式，并結合(8)式得到材料去除模型：

(14)

(14)式可以簡化為

(15)

2 快速拋光材料去除模型驗證

2.1 驗證流程

圖4所示為材料去除模型驗證流程，首先將壓力p1與p2下通過實驗獲得的材料去除量MRR1與MRR2分別代入模型，兩者相除并利用數學運算軟件MathCAD，結合標準正態分布的性質，計算可得C2值。將其他實驗壓力值及計算得到的C2值代入模型得到理論材料去除量，將實際測到的材料去除量與理論計算的材料去除量作對比，求得誤差，同理求出不同實驗壓力下的材料去除量及誤差，繼而驗證模型的正確性。

圖4 MRR模型驗證流程Fig.4 Verification process of MRR formula

2.2 實驗樣品制備

實驗使用福建省三明機床有限公司產PKD330快速拋光機，采用正交實驗進行材料去除模型的驗證。從推導出的模型可以看出，影響材料去除的因素主要有拋光墊、拋光液、元件、相對速度和施加壓力。由于在模型的驗證計算過程中相對速度被約掉，而施加壓力作為實驗條件，所以影響因素只剩3個，即拋光墊、拋光液和元件。3個因素各選擇3個水平，各因素的水平選擇見表1. 對于拋光墊，考慮到拋光墊對于捕獲磨粒數的影響，因此拋光墊性能特別是密度和肖氏硬度有一定差別；對于光學元件，選擇了神光Ⅲ裝置中最常用的熔石英和K9玻璃，與微晶陶瓷玻璃一起作為實驗元件；對于拋光液，考慮到初拋和精拋等不同階段使用的粒徑不一樣，因此也根據實際的工程應用加以選擇。

表1 水平因素編碼Tab.1 Level factor coding

實驗所用拋光墊的參數如表2所示。由表2可知，LP66-1.52、LP-88 和GR-35拋光墊在填充物、密度、肖氏硬度和開槽條件方面都有區別，3種拋光墊的表面微觀形貌掃描電子顯微鏡(SEM)圖如圖5所示，由日本日立公司產SU70場發射SEM測得。從SEM圖上可以看到，拋光墊表面上分布著氣孔，氣孔與氣孔之間的峰點在表面呈現規律性分布。實驗所用拋光顆粒粒徑均由珠海歐美克儀器有限公司產LS603激光粒度分析儀測得。Al2O3拋光顆粒平均粒徑為20 μm，如圖6所示，CeO2拋光顆粒平均粒徑為1 μm，SiO2拋光顆粒平均粒徑為40 μm，3種拋光液濃度均為20%. 實驗所用的微晶玻璃、熔石英玻璃和K9玻璃尺寸均為30 mm×30 mm×5 mm.

選用L9(34)作為實驗的正交表，具體正交實驗方案如表3所示。

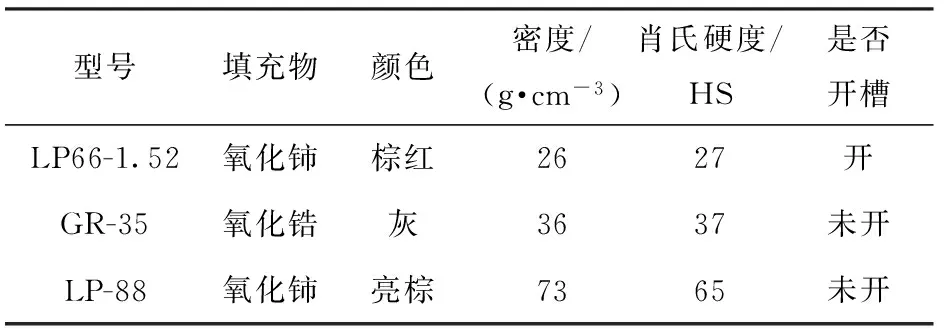
表2 拋光墊參數Tab.2 Polishing pad parameters

圖5 拋光墊的表面微觀形貌Fig.5 Surface microstructure of polishing pad

圖6 粒度分布圖Fig.6 Particle size distribution

每組實驗在9 N、12 N、15 N和18 N不同壓力條件下進行，加工時間均為1 h，元件和拋光盤轉速均為100 r/min. 拋光前后使用精密天平測量每塊光學元件的質量，用于計算材料去除。

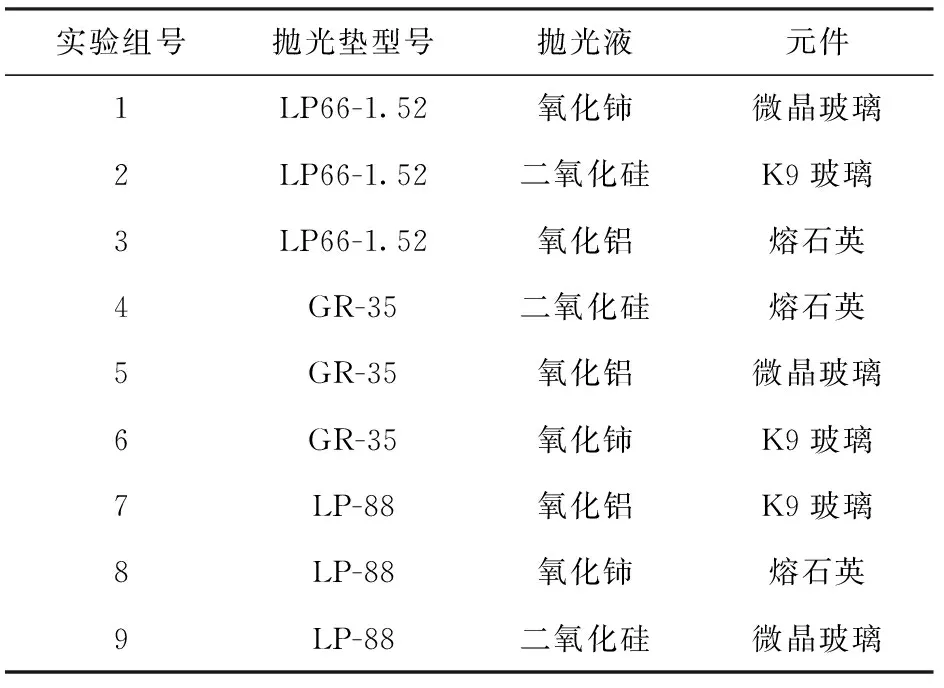
表3 實驗方案Tab.3 Experimental schemes

2.3 實驗數據分析

經過36組實驗，使用精密天平測得每塊光學元件拋光前后的質量，得到每塊光學元件的材料去除量，獲得實驗數據如表4所示。

表4 MRR 實驗數據Tab.4 Experimental data of MRR mg

從表4中可以看到，拋光墊的材料性能(包括密度、肖氏硬度和開槽條件等)、元件的種類和拋光顆粒的粒徑都對材料去除量有影響。例如K9玻璃的3組實驗，實驗7所使用的LP-88拋光墊相比較實驗6所使用的GR-35拋光墊肖氏硬度要大，填充在拋光墊上的拋光顆粒較少，獲得的材料去除量理論上應該較低，但是前者拋光墊密度較大，拋光墊峰點數較多，且使用的Al2O3拋光顆粒粒徑也大于后者所使用的CeO2拋光顆粒，從表4中可以看出，實際的前者材料去除量較大。因此，材料去除量是幾種因素共同作用的結果。

為了不失一般性，在表中的每組實驗中任選兩個材料去除量作為原始數據代入到模型中計算理論材料去除量，計算后得到的理論數據以及相對誤差如表5所示。

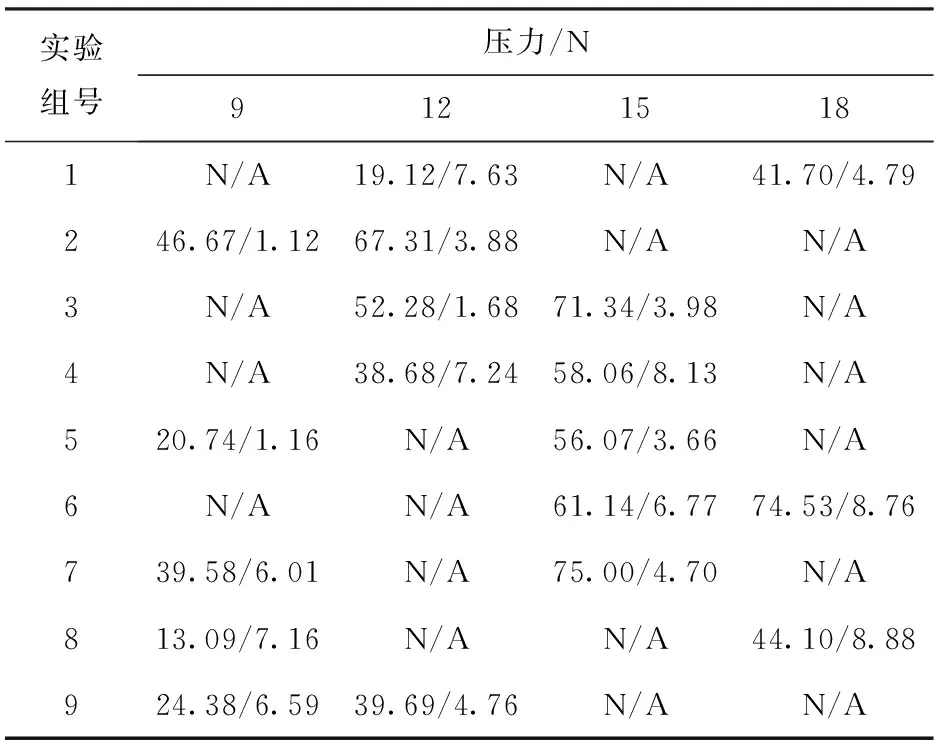
表5 理論數據及相對誤差Tab.5 Theoretical data and relative errors

注：表中數據為MRR(mg)/ΔMRR(%)；每組實驗中兩處N/A代表該組實驗中用于計算理論MRR的兩個原始數據。

從表5中可以看到，18組材料去除量誤差都在9%以內，最大的達到8.88%，最小的達到1.12%. 考慮到實驗中機床的運動誤差、對刀誤差以及天平測量誤差等誤差因素，通過材料去除模型計算出來的材料去除量同實際實驗得到材料去除量較為吻合，從而驗證建立的光學元件快速拋光材料去除模型的正確性。需要指出的是，實驗中所使用3種玻璃元件尺寸較小，質量比較輕，因此材料去除量誤差的敏感度也比較大。在相同元件和其他加工條件相同的實驗條件下，快速拋光依靠其自主運動性和外界施加壓力，拋光效率大約是傳統環形拋光的5～10倍左右?？刂圃倪\動路徑、施加壓力以及其他加工條件，400 mm直徑的圓形光學元件面型精度可以達到0.5個波長，表面粗糙度可以達到1 nm以內，這些內容將在以后的論文中專門發表。

3 結論

1)針對Luo等基于磨粒磨損機制所建立的材料去除模型的不足，從單顆磨粒受力和拋光墊峰點捕獲的磨粒數出發，獲得量化的單顆磨粒瞬時切除體積和拋光接觸區參與有效磨粒數，從而建立一種光學元件快速拋光材料去除模型。

2)通過正交實驗，驗證了在不同類型光學元件、拋光墊和拋光液條件下，理論預測值與實驗值相比誤差控制在9%以內，拋光實驗的結果與理論預測的結果比較吻合，從而驗證了本文所建立的光學元件快速拋光材料去除模型的正確性。

3)以本文建立的去除模型為基礎，可以根據預測的研磨階段亞表面缺陷深度，在拋光階段嚴格控制加工參數，避免盲目加工，極大縮短加工時間，從而提高加工效率，滿足光學元件批量生產的目標。

References)

[1] 趙東峰, 鄔融, 林尊琪, 等. 超聲波輔助酸蝕提高熔石英損傷閾值[J]. 強激光與粒子束, 2015, 27(1):105-110. ZHAO Dong-feng, WU Rong, LIN Zun-qi,et al.Acid etching combined with ultrasonic for improving laser damage threshold of fused silica[J]. High Power Laser and Particle Beams, 2015, 27(1):105-110.(in Chinese)

[2] 王洪祥, 朱本溫, 陳賢華, 等. 拋光工藝參數對熔石英元件低頻面形精度的影響[J]. 強激光與粒子束, 2015, 27(4):042001-1-042001-5. WANG Hong-xiang, ZHU Ben-wen, CHEN Xian-hua, et al. Impact of polishing process parameters on the low frequency surface accuracy of fused silica optics[J]. High Power Laser and Particle Beams, 2015, 27(4):042001-1-042001-5.(in Chinese)

[3] Mu Y, Zhuang Y, Sampurno Y,et al. Effect of pad groove width on slurry mean residence time and slurry utilization efficiency in CMP[J]. Microelectronic Engineering, 2016, 157:60-63.

[4] Suratwala T I, Wong L L, Miller P E, et al. Sub-surface mechanical damage distribution during grinding of fused silica[J]. Journal of Non-Crystalline Solids, 2006, 352: 5601-5617.

[5] Luo J F, Dornfeld D A. Material removal mechanism in chemical mechanical polishing: theory and modeling[J]. IEEE Transactions on Semiconductor Manufacturing, 2001, 14(2):112-133.

[6] Runnels S R, Eyman L M. Tribology analysis of chemical mechanical polishing[J].Journal of Electrochemical Society, 1994, 141(6):1698-1701.

[7] Borst C L, Thakurta D G, Gill W N, et al. Surface kinetics model for SiLK chemical mechanical polishing[J]. Journal of Electrochemical Society, 2002, 149(2):118-127.

[8] Zhao Y W,Chang L, Kim S H. A mathematical model for chemical mechanical polishing based on formation and removal of weakly bonded molecular species[J]. Wear, 2003, 254(3/4):332-339.

[9] Zhao Y W,Chang L. A micro-contact and wear model for chemical-mechanical polishing of silicon wafers[J]. Wear, 2002, 252(3/4):220-226.

[10] Moon Y. Mechanical aspects of the material removal mechanism in chemical mechanism polishing (CMP)[D]. Berkeley: University of California at Berkeley, 1999.

[11] Jiun Y L. Mechanics, mechanisms, and modeling of the chemical mechanical polishing process[D]. Massachusetts: Massachusetts Institute of Technology, 2001.

[12] Yang W, Guo Y B, Li Y G, et al. Pressure and velocity dependence of the material removal rate in the fast polishing process[J]. Applied Optics, 2007, 47(33):6236-6242.

[13] Marquez J J, Perez J M, Rios J, et al. Process modeling for robotic polishing[J]. Journal of Materials Processing Technology, 2005, 159(1):69-82.

[14] Cook L M. Chemical processes in glass polishing[J]. Journal of Non-Crystalline Solids, 1990, 120(1/2/3):152-171.

[15] Zhang F. Submicron particle adhension and removal in chemical-mechanical polishing and wafer cleaning process[D]. Potsdam: Clarksom University, 2002.

[16] Greenwood J A, Williamson J B P. Contact of nominally flat surfaces[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1966, 295(1442): 300-319, 1996.

Research on Material Removal Model of Optical Elements Based on Fast Polishing Technology

LIN Tao1, YANG Wei1, WANG Jian2

(1.School of Aerospace Engineering, Xiamen University, Xiamen 361005, Fujian, China; 2.Research Center of Laser Fusion, China Academy of Engineering Physics, Mianyang 621900, Sichuan, China)

In order to accurately control the material removal in polishing stage, and achieve the deterministic polishing processing of toptical element, the quantitative mean volume removed by a single particles per unit time and the number of the active particles on the wafer-pad interface are obtained from the force applied on an abrasive particle and the number of all particles on the wafer-pad contact area. An optical element fast polishing material removal model is established based on the analysis of fast polishing principle and fast polishing material removal mechanism. Research shows that, under the experimental conditions of different polishing liquids, polishing pads and optical elements, the theoretically predicted results of the material removal model are well coincident with the experimental results, and the error of material removal can be controlled within 9%. The proposed model is verified to be suitable for the optical element fast polishing technology, thus deterministically controling the fast polishing time and efficiency.

manufacturing technology and equipment; optical element; fast polishing; material removal model

2016-04-22

國家自然科學基金項目(51675453)；福建省高等學校創新能力提升計劃項目(2013年)

林濤(1989—)，男，碩士研究生。E-mail: 519023733@qq.com

楊煒(1981—)，男，助理教授，碩士生導師。E-mail:oncefly@126.com

TN205

A

1000-1093(2017)03-0527-07

10.3969/j.issn.1000-1093.2017.03.015