優化藥物制劑工藝的多種數據處理方法的研究
李乃智
摘 要:目前在藥物制劑領域中對其運用的數據處理方法種類較多,本文主要以領域內相關的文獻資料作為分析基礎,對其中方差分析、多元回歸分析等多種數據處理方法進行分析及總結,對這些數據處理方法在藥物制劑中可以起到的優化作用進行探討,從而確定其在藥劑質量控制中的作用。
關鍵詞:藥物制劑;數據處理;分析;作用
目前科技的快速發展決定了各類科學理論知識在一定程度上會相互滲透、相互作用,而利用數據處理方法對藥物制劑工藝進行優化是領域內重點研究的方向之一。由于在藥物制劑生產的過程中,其流程、方法、時間、溫度、配比、PH值等都可能影響藥物的實際藥效,因此在藥物制劑工藝使用的過程中需要對各項指標及方法標準進行確定。
一、多種數據處理方法的作用
在實際中使用不同的數據處理方法會對藥物制劑實驗結果產生不同的影響,對藥物制劑中單指標及多指標采用的數據處理方法也有所不同,根據目前藥物制劑工藝優化采用的數據處理方法來看,其單指標多采用方差分析法,這種分析方法在多指標數據中并不適用,單獨使用會使數據出現偏差,無法起到優化藥物制劑工藝的作用,因此可以選擇數據處理方法的聯用來提高數據結果準確性,為工藝優化提供數據支持。
二、多種數據處理方法
1.方差分析-多指標綜合加權評分法
在藥物制劑中采用指標是為了保證制劑工藝的準確性、科學性、標準性及規范性,因此在多指標數據的處理上需要根據實際進行加權處理,從而對其進行綜合的評分。對各評價指標按其相對重要程度分配系數,然后以累加法、連乘法或加乘法累計總分,根據總分高低排出優劣順序。目前方差分析-多指標綜合加權評分法在實際的使用中計算方法較為繁瑣,但是其在藥物制劑工藝的評價上有突出重點、結果準確等優點,綜合加權評分法所具有的結果分析的特點可以選出方案中最佳的工藝方法。雖然采用方差分析-多指標綜合加權法能達到優化工藝的效果,但存在不足。首先,方差分析只依賴于指標值,一旦某點或幾個點的指標值誤差很大,勢必會影響計算結果的可靠性,從而影響數據結果分析的準確性;其次是對實驗點的誤差大小無法判斷;再次,在進行工藝優化時只能從正交或均勻設計表中找出最好點的實驗條件作為優化條件,但這未必是真正的優化條件。
2.多元回歸分析-效應面法響應面法
這種組合式數據處理方法結合了數學運算及統計方法的優點,其建模可以對藥物制劑中的多指標數據進行組合分析。采用多元回歸結合效應面法計算,首先可彌補正交方差計算的不足,如回歸方程既能明確每個因素對指標的影響,又可判斷實驗點的實驗誤差,更有利于結果解釋和工藝條件的優化;其次,多元回歸分析所需要的試驗數量較少,且對于多指標中參數之間的作用可以有效的減少,因此在進行數據處理上較一些其他數據處理方法更加有效,所得計算結果也更加精確。該分析方法符合一般數學多元回歸模型:
Y=b0+b1p+b2m+b3pm+b4p2+b5m2
b0~b5是評估模型的參數,p、m表示自變量,Y表示因變量,該多元回歸模型能預測自變量與因變量的關系。然后再通過建立連續變量曲面模型,精確地表述因素與響應值之間的關系,對影響制劑工藝的因素水平進行優化和評價。
3.人工神經網絡系統(ANN)
ANN是理論化的人腦神經網絡的數學模型,能很好地預測多因素多水平非線性關系,很適于解決多元同時優化的問題,廣泛應用于藥學領域。ANN是復雜的非線性網絡模型,不僅可以省略復雜的統計,就能把自變量和因變量結合起來,而且在模擬和預測時,結果偏差均較RSM小。ANN在優化制劑工藝方面,包括網絡模型的構建與訓練、實驗條件仿真及優化兩過程。
4.多維空間三角形面積法
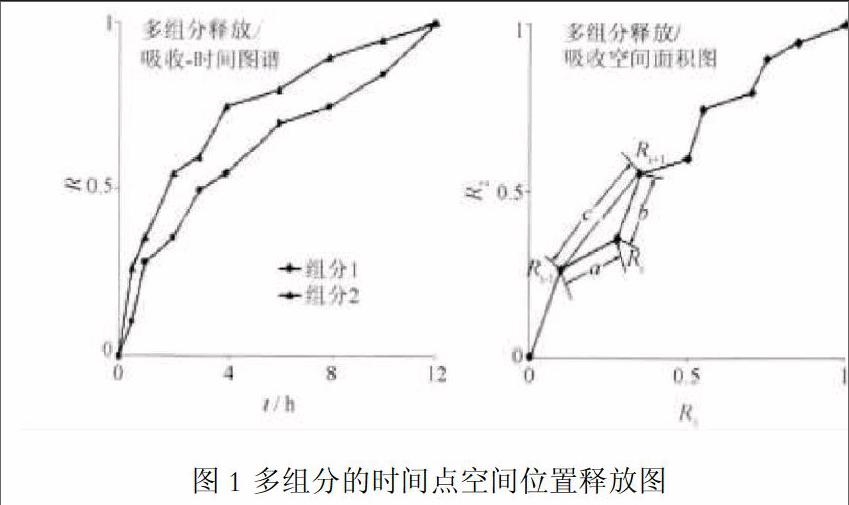
多維空間三角形面積法,即任一時間點,多組分釋放度或多組分吸收度是多維空間中的一個點,連續3個時間點連線的三角形面積反映了多組分釋放或吸收的動力學變化特征。通過計算多維空間中點與點的距離,得到任意連續3個時間點(釋放/吸收)形成三角形的3個邊長,進而計算其面積(圖1)。以釋放度三角形面積累計值-吸收度三角形面積累計值的相關性來表征藥物的多組分釋放-吸收體內外相關性,而大量文獻報道,體內外相關性可用于評價及優化藥物制劑工藝。所以,多維空間三角形面積法作為一種新的數據處理方法,在優化藥物制劑工藝方面,將會有更廣闊的應用前景。
三、展望
藥物制劑工藝是非常復雜的過程,方差分析-多指標綜合加權評分法、多元回歸分析-效應面法、ANN及多維空間三角形面積法都能揭示多因素多水平之間的規律,可以達到優化工藝的目的。
在保證指標值誤差不是很大的情況下,選用方差分析-多指標綜合加權評分法進行優化更為簡單;RSM數據分析結果太依賴于具體的非線性方程,且在模型擬合方面較為困難,所以,在聯系不是很復雜且對結果要求不是很高的情況下,運用RSM法進行優化更為實用;ANN是以實驗數據為基礎,經過有限次迭代計算而獲得的一個反映實驗數據內在規律的數學模型,且無需目標函數具備明確的數學表達式,并且模型的建立與尋優的過程都可以利用數據可視化技術以直觀的圖形展現出來,為解決多維非線性系統的優化問題提供了一個全新而有效的途徑;多維空間三角形面積法作為一種新的數據處理方法,適合研究物質組分比較明確,且組分在體內外均可檢測到的多組分藥物。通過大量實驗研究及查閱相關代謝組學文獻,擬合出代謝組學動態數學模型,即以代謝產物含量為檢測指標,來考察影響制備的主要因素,可用于優化多組分中藥的制備工藝。目前,多維空間三角形面積法和代謝組學動態數學模型在國內極為少見,隨著多學科交叉的滲透以及制劑工藝研究工作者研究水平的不斷提高,這兩種方法必將得到更廣泛的應用。
綜上所述,上述的幾種數據處理方法在藥物制劑中較為常見,根據實際需要應用適當的數據處理分析方法可以補足制劑工藝中存在的不足,并在科學的基礎上對這些工藝進行進一步的優化,完善藥物制劑工藝,可以為藥物制劑的質量提供一定的保障。
參考文獻:
[1] 譚素玲.化學藥物制劑處方及工藝研究[J].科研,2016(12):00036-00036.
[2] 田永紅.藥物制劑工藝分析[J].中國科技博覽,2013(17):234-234.
[3] 徐宇虹,方中堅.藥物制劑的優化篩選方法,CN103656688A[P].2014.

