CO2/CH4在煤儲層中擴散規律的分子動力學模擬*
林海飛,劉靜波,嚴 敏,白 楊,劉寶莉
(1. 西安科技大學 安全科學與工程學院,陜西 西安 710054; 2. 教育部西部礦井開采及災害防治重點實驗室,陜西 西安 710054)
0 引言
煤層瓦斯含量是礦井瓦斯涌出量預測、瓦斯抽采、煤與瓦斯突出防治的基礎,正確測試瓦斯含量的關鍵之一是明確甲烷在煤體內的擴散特性[1-2]。近年來,大量學者通過理論分析、試驗研究以及數值模擬等方法對瓦斯在煤體內的擴散特性進行了深入研究,取得了豐碩的成果。李志強[3]、易俊[4]通過建立甲烷的擴散模型,利用新型擴散模型計算了擴散系數,與實驗吻合較好;劉彥偉,陳磊[5-6]等人分別研究了水分和溫度對甲烷擴散系數的影響,研究結果表明:隨著水分的增大,甲烷的擴散系數的減小幅度降低;溫度對甲烷的擴散系數有促進作用;蘇恒[7]、王瑞[8]、劉炎杰[9]等人考率了溫度、壓力和煤變質程度3種因素對甲烷擴散的影響,結果表明低變質程度的煤中,孔隙連通性好,甲烷更易于擴散,而相同條件下,溫度和擴散系數呈正比關系,壓力增加,擴散系數降低;劉中民、鄭祿彬[10]等人在考慮吸附質分子濃度的影響下,提出了擴散系數與濃度相關的擴散方程,并通過測定吸附質分子在分子篩上的擴散系數驗證了該方程; Kuniyasu Ogawa[11]等人研究了吸附在填充有分子篩的沸石中的水分子的擴散特性,通過比較沸石不同微孔內的水分子濃度得出了水在沸石中的擴散系數值;Gregory Staib[12]等人以2種不同煤結構為基礎,通過獲取2種模型的吸附動力學數據,分別研究了壓力和2種模型擴散系數的關系;Civan F[13]等人通過理論分析得出了另一種計算克努森模型下甲烷在頁巖擴散系數的計算方法。
盡管前期國內外學者對于煤體內甲烷的擴散特性影響研究較多,但由于煤儲層中所含氣體為CH4,CO2等多組分氣體,目前對于CO2與CH4混合氣體在煤儲層中擴散的影響機制研究相對較少。鑒于此,筆者從分子角度出發,采用分子動力學模擬的方法研究CO2與CH4濃度比、溫度、氣體壓力和儲層孔徑等4種因素對甲烷擴散系數的影響,以期為進一步揭示甲烷在煤中的擴散機理提供一定依據。
1 煤儲層CO2/CH4混合氣擴散的數值模型
1.1 模擬方法
采用分子動力學模擬的方法,研究CO2與CH4濃度比、溫度、氣體壓力和儲層孔徑4種因素對CH4在煤中擴散系數的影響。為計算甲烷在煤中的擴散系數D,首先使CH4/CO2在煤體中吸附飽和,同時為防止超臨界狀態氣體密度增大對擴散系數的影響,最高吸附平衡壓力設置為5 MPa。根據均方位移法和愛因斯坦方程[14-15]可知原子的擴散系數D和均方位移MSD存在以下關系:
(1)
式中:t為模擬時間;r(t)為t時刻CH4分子的位移,r(0)為初始時刻CH4的位移;[r(t)-r(0)]2為CH4的均方位移MSD;D為CH4的擴散系數。
1.2 擴散模型的建立
煤中的孔隙結構非常復雜,許多學者通過測試煤的孔隙結構發現:煤中包含一端封閉的不透氣孔、墨水瓶型孔、平行板狀狹縫型孔、傾斜板狀狹縫型孔,并且以狹縫孔居多[16-17];另一方面,狹縫型孔的建模相對其他幾種類型孔隙難度較低,為了便于研究,選用了狹縫型孔。綜上所述,利用狹縫型孔代表煤中的復雜孔隙結構。同時,以不同寬度的石墨狹縫來表征煤儲層中的不同尺寸孔。由于分子動力學的計算過程需要比較穩定的吸附構型,因此以5層石墨烯結構作為吸附基底,利用Material Studio 7.0分別建立了石墨狹縫、CH4以及CO2的分子結構。圖1為4種不同狹縫寬度的石墨狹縫結構,狹縫寬度分別為10?,20?,40?,50?(10?=1 nm);石墨狹縫在x和y方向上的尺寸分別為Lx=42.61?,Ly=44.28?。優化后的CH4和CO2分子的結構參數如表1所示。

圖1 4種不同寬度的石墨狹縫模型Fig.1 Four different width of slit pore model

吸附質分子鍵長/?鍵角/?CH41.0986109.471CO21.16180
為了獲得CH4在石墨狹縫中的擴散模型,利用軟件中的Sorption模塊使CH4/CO2吸附飽和,利用該模塊中的fix pressure功能可以準確獲得不同平衡壓力下石墨狹縫的吸附量,進而可以獲得不同CO2與CH4濃度比、儲層孔徑、溫度、氣體壓力下的吸附飽和構型,在Discover模塊下對該吸附飽和的構型進行分子動力學計算。
由式(1)可知,擴散系數D等于MSD-t直線斜率的1/6,因此根據MSD-t曲線可以計算出不同條件下的甲烷在石墨狹縫中的擴散系數。
1.3 初始及邊界條件
在分子動力學模擬過程中,選擇COMPASS力場,非鍵non-bond設置為基于范德華作用;模擬方法選擇基于原子,計算精度設置為中等,截斷半徑cut off一般與原子之間的平衡距離有關,取9.5?;采用NVT系綜,時間步長為0.5 fs,動力學時間為5 ps,并且每500步輸出一個最穩定構型。
邊界條件采用周期性邊界條件,如圖2所示為二維周期性邊界條件下晶胞的分布情況,中間的晶胞對應實施模擬的區域,其周圍有8個最臨近晶胞,當模擬區域中有原子運動到盒子外面,則會有與之對應的原子從對應方向進入模擬區域。

圖2 周期性邊界條件Fig.2 Periodic boundary condition
2 模擬結果分析
2.1 CO2與CH4濃度比對甲烷擴散系數的影響
當溫度在313 K,孔徑寬2 nm,壓力為3 MPa,CO2和CH4濃度比為0∶1,1∶1,3∶1和5∶1時,甲烷在石墨狹縫中擴散的MSD-t曲線如圖3所示,根據擴散系數和均方位移的關系計算出相同條件不同壓力下甲烷的擴散系數值如表2所示。

圖3 不同CO2濃度下CH4擴散的MSD曲線Fig.3 MSD curve of gas diffusion in different concentration

CO2/CH4濃度比0∶11∶13∶15∶1擴散系數D/(10-8m2/s)1.881.521.251.10
將計算得到的擴散系數數據和CO2濃度進行擬合,擬合結果如圖4所示,兩者擬合關系如式(2)所示。
DCH4=0.81e-0.51CCO2+1.06
R2=0.989
(2)
式中:CCO2代表CO2分子的濃度。

圖4 CO2濃度和CH4擴散系數的關系Fig.4 Relationship between CO2 concentration and gas diffusion coefficient
由圖4及式(2)可知,CH4的擴散系數隨著CO2濃度的增大而減小,這主要是因為隨著CO2分子數的增大,大部分的吸附位點被吸附性強的CO2分子占據,少數吸附能力較弱的位點由CH4分子占據,即CO2的吸附量高于CH4,CH4分子在CO2分子以及狹縫壁面的雙重作用下,擴散阻力增大,因此CH4的擴散系數有下降規律,且和CO2濃度呈指數函數關系。
2.2 氣體壓力對CH4擴散系數的影響
當溫度在313 K,孔徑寬2 nm,CO2和CH4濃度比為3∶1時,儲層壓力在2 MPa,3 MPa,4 MPa和5 MPa下,CH4在石墨狹縫中的擴散的MSD-t曲線如圖5所示,計算得到的擴散系數值如表3所示。

圖5 不同氣體壓力下CH4擴散的MSD曲線Fig.5 MSD curve of gas diffusion in different gas pressure

氣體壓力P/MPa2345擴散系數D/(10-8m2/s)2.401.250.680.51
將計算得到的擴散系數數據和壓力進行擬合,擬合結果如圖6所示,兩者擬合關系如式(3)所示。

圖6 氣體壓力和CH4擴散系數的關系Fig.6 Relationship between gas pressure and gas diffusion coefficient
(3)
式中:P代表煤氣體壓力。
由圖6及式(3)可以看出,CH4的擴散系數隨著氣體壓力的增大而減小,這主要是因為隨著吸附氣體壓力的增大,煤模型出現小范圍的膨脹變形,CH4的擴散通道狹窄使其擴散性能降低;另一方面,隨著壓力的增大,游離相和吸附相CH4的密度增大,CH4分子之間以及CH4分子和狹縫壁面結合的更加緊密,擴散性能同樣降低。壓力對CH4擴散系數影響的模擬結果和蘇恒[7]、王瑞[8]、劉炎杰[9]等人研究成果相一致。
2.3 溫度對CH4擴散系數的影響
當壓力在3 MPa下,孔徑寬2 nm,CO2和CH4濃度比為3∶1時,溫度分別在323 K, 313 K, 303 K以及293 K下,CH4在石墨狹縫中的擴散的MSD-t曲線如圖7所示,計算出相同條件不同溫度下CH4的擴散系數值見表4。
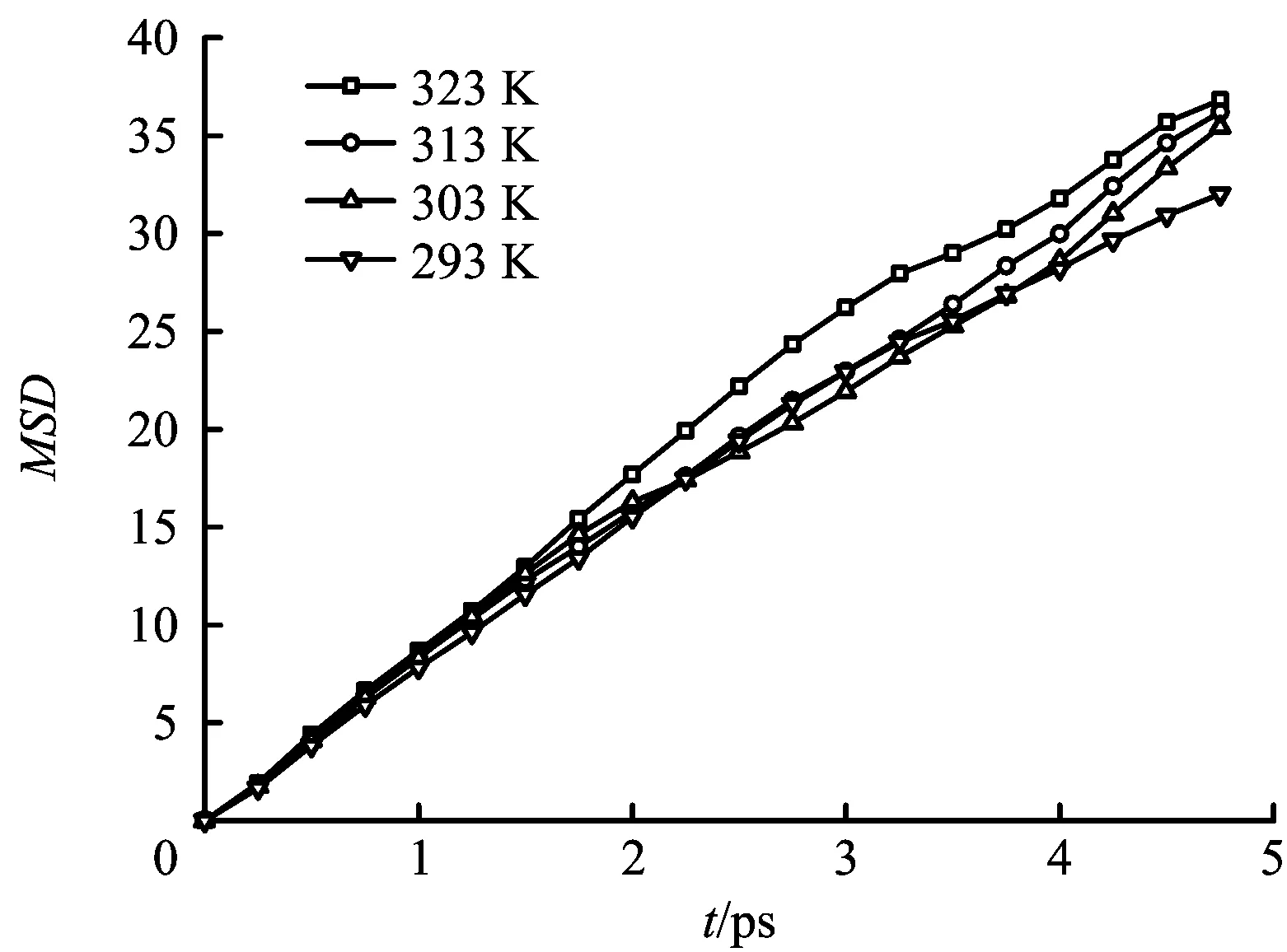
圖7 不同溫度下CH4擴散的MSD曲線Fig.7 MSD curve of gas diffusion in different temperature

溫度T/K293303313323擴散系數D/(10-8m2/s)1.151.191.251.31
將計算得到的擴散系數數據和溫度進行擬合,擬合結果如圖8所示,兩者擬合關系如式(4)所示。
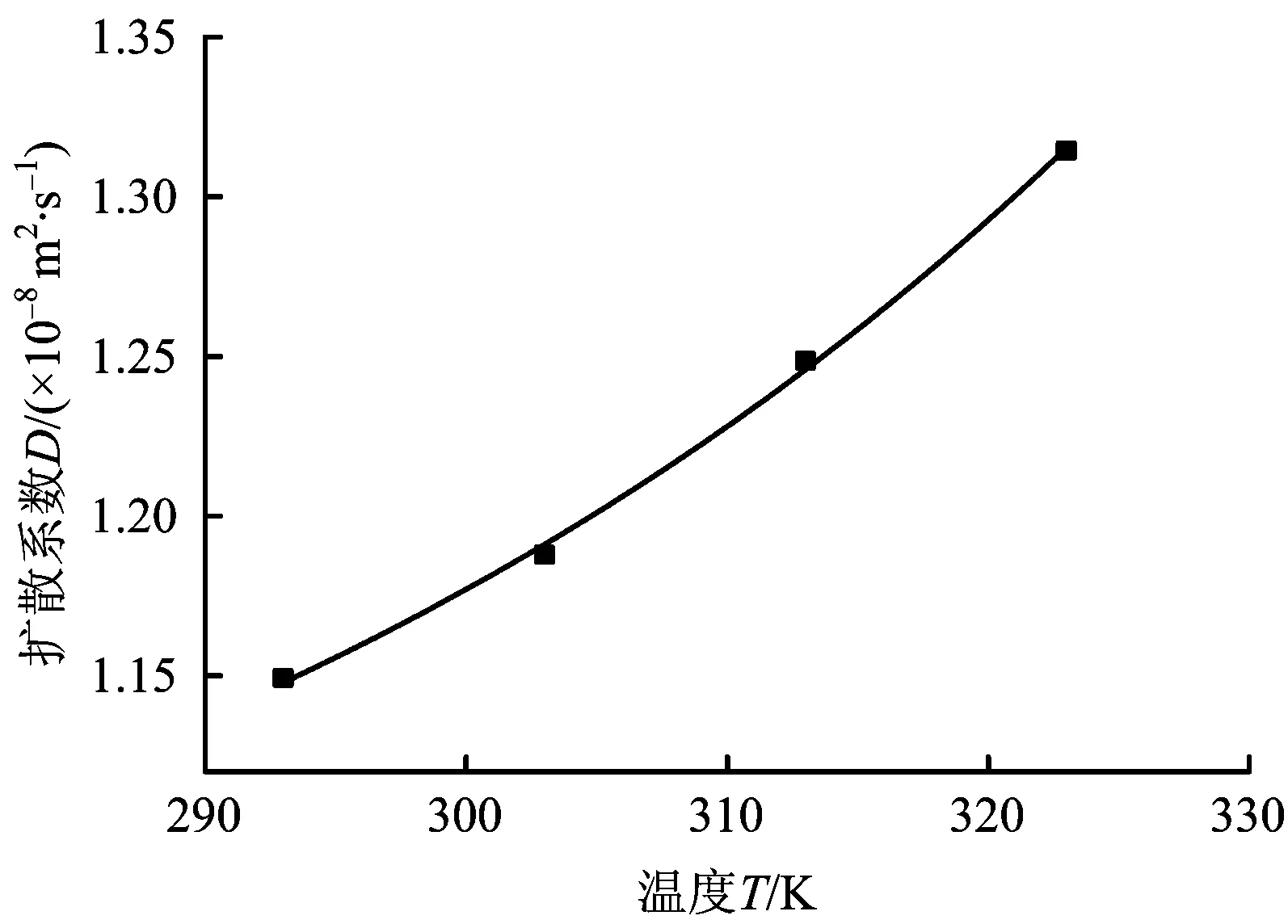
圖8 溫度和CH4擴散系數的關系Fig.8 Relationship between temperature and gas diffusion coefficient
(4)
由圖8及式(4)可以發現:溫度對CH4的擴散具有明顯的促進作用,這主要體現在均方位移和分子的平均自由程隨溫度的變化關系上。首先溫度的升高使CH4分子的熱運動效應增強,CH4分子的均方位移增大,擴散系數增大;同時CH4分子的平均自由程也會隨著溫度的升高而增大,同樣有助于加快CH4的擴散速率;這與陳磊[6]的研究結果符合。
由模擬結果可以發現隨著溫度的升高,擴散系數增加的并不明顯,出現這種情況的原因主要是石墨狹縫結構將煤的孔隙結構,比表面積等結構理想化,溫度對這些因素的影響并不能真實的體現,從而導致擴散系數隨溫度的變化沒有實驗室測定的明顯。
2.4 儲層孔徑對CH4擴散系數的影響
當溫度在313 K下,壓力為3 MPa,CH4和CO2濃度比為1∶3時,儲層孔徑為15 nm,25 nm,45 nm,5 nm下,CH4在石墨狹縫中的擴散的MSD-t曲線如圖9所示,計算出相同條件不同孔徑下CH4的擴散系數值如表5所示。

圖9 不同儲層孔徑下CH4擴散的MSD曲線Fig.9 MSD curve of gas diffusion in different aperture

孔徑d/nm1245擴散系數D/(10-8m2/s)0.581.251.722.00
將計算得到的擴散系數數據和儲層孔徑進行擬合,擬合結果如圖10所示,兩者擬合關系如式(5)所示。
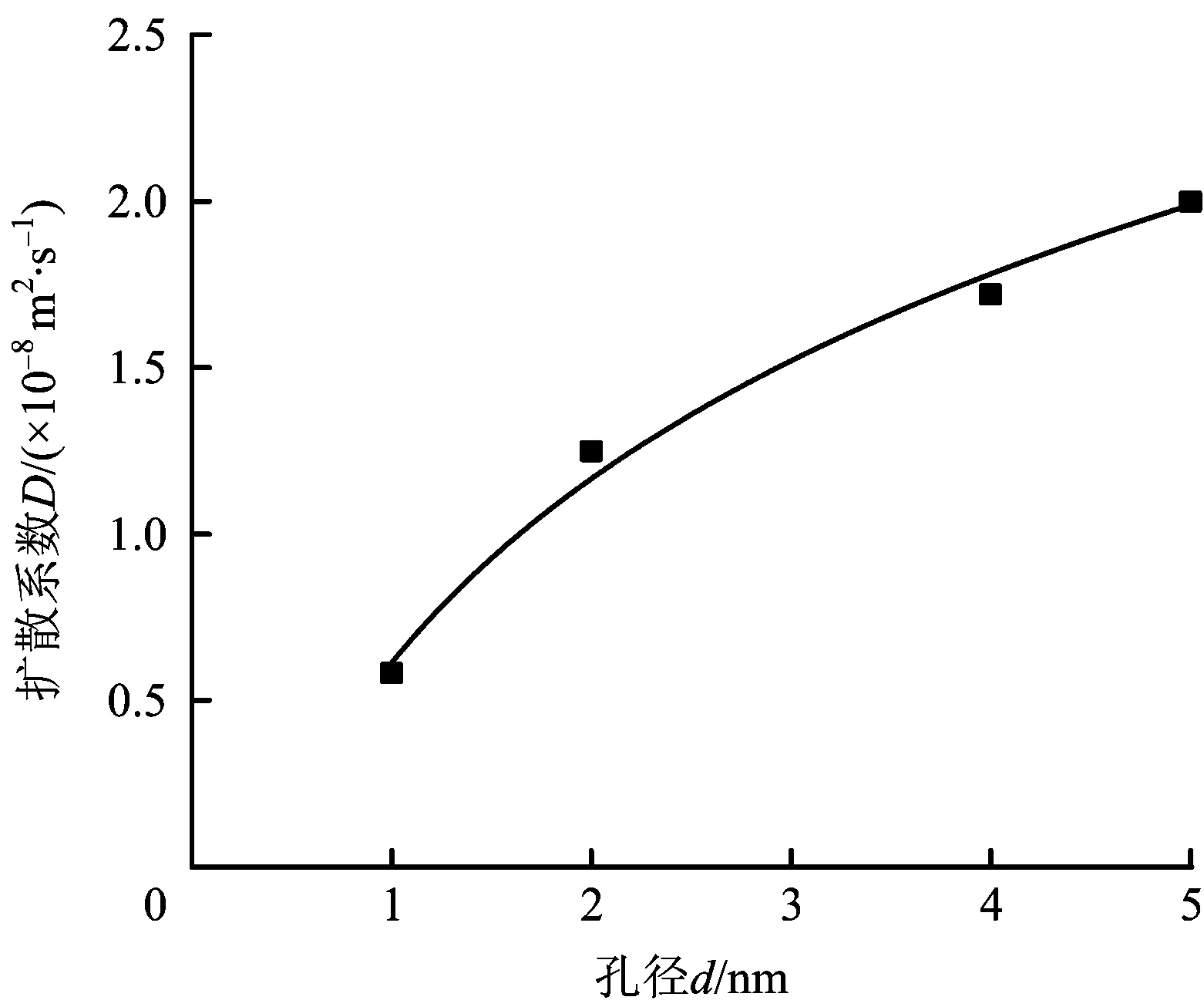
圖10 儲層孔徑和CH4擴散系數的關系Fig.10 Relationship between aperture and gas diffusion coefficient
(5)
由圖10及式(5)可知,CH4的擴散系數隨著儲層孔徑的增大而增大且呈現出對數函數關系,這是因為當狹縫寬度較小時壁面效應較強,CH4分子受到上下壁面的雙重作用,擴散能力較低,而隨著狹縫寬度的增大,CH4分子由雙壁面疊加受力變為單側壁面受力,CH4分子和壁面之間的作用力降低,擴散能力增強,隨著孔徑的進一步增大,雙側壁面效應進一步減弱直到可以忽略不計,因此擴散系數增大的越來越慢;另一方面,孔徑的增大提供了CH4運移的通道,擴散能力增強。在上述2種機制的共同作用下導致了CH4的擴散系數隨儲層孔徑的增大呈對數增加關系。
隨著孔徑繼續增大,CH4的擴散系數是否會趨向一個極限值,課題組將會在后期展開進一步的研究。
3 結論
1)CO2的競爭吸附作用會使得CH4的吸附量降低,吸附量較小的CH4分子在狹縫壁面和CO2分子的共同作用下,擴散能力降低且擴散系數和CO2濃度呈指數函數關系。
2)氣體壓力越大,吸附相和游離相CH4的密度均增大,CH4分子之間,CH4和狹縫壁面結合的更緊密,擴散系數越小并呈冪函數關系,擴散性能也越低。
3)溫度的升高增加了CH4分子的均方位移和分子平均自由程,CH4的擴散系數增大且與溫度呈指數函數關系;理想化的孔隙結構導致了溫度對擴散系數的影響程度低于實驗測定的結果。
4)隨著儲層孔徑的增大,CH4分子的受力由雙側壁面疊加效應轉變為單側壁面受力,擴散系數增大且與孔徑呈現對數函數關系。
[1]]楊書召,張瑞林. 煤與瓦斯突出沖擊波及瓦斯氣流所致傷害研究[J].中國安全科學學報,2012,22(11):62-66.
YANG Shuzhao, ZHANG Ruilin. Research on injuries due to shock wave and gas flow from coal and gas outburst[J]. China Safety Science Journal, 2012,22(11):62-66.
[2]岳高偉,王兆豐,康博. 低溫環境煤的瓦斯擴散系數時變特性[J].中國安全科學學報,2014,24(2):107-112.
YUE Gaowei, WANG Zhaofeng, KANG Bo. Time-varying characteristics of gas diffusion coefficient in low temperature environment [J]. China Safety Science Journal, 2014, 24(2): 107-112.
[3]李志強,劉勇,許彥鵬,等. 煤粒多尺度孔隙中瓦斯擴散機理及動擴散系數新模型[J].煤炭學報,2016,41(3):633-643.
LI Zhiqiang, LIU Yong, XU Yanpeng, et al. Gas diffusion mechanism in multi-scale pores of coal particles and new diffusion model of dynamic diffusion coefficient[J].Journal of China Coal Society, 2016,41(3):633-643.
[4]易俊,姜永東,鮮學福. 煤層微孔中甲烷的簡化雙擴散數學模型[J].煤炭學報,2009,34(3):355-360.
YI Jun, JIANG Yongdong, XIAN Xuefu. Predigested bidispere diffusion mathematical model of methane in coal micro pores[J].Journal of China Coal Society, 2009,34(3): 355-360.
[5]劉彥偉, 張加琪, 劉明舉, 等. 水分對不同變質程度煤粒瓦斯擴散系數的影響[J]. 中國安全生產科學技術, 2015, 11(6): 12-17.
LIU Yanwei, ZHANG Jiaqi, LIU Mingju, et al. Influence of moisture content on gas diffusion coefficient of coal particles with different metamorphic degree[J].Journal of Safety Science and Technology, 2015, 11(6): 12-17.
[6]陳磊,林鴻,陶文銓. 溫度對質子交換膜擴散性能影響的分子動力學模擬[J].西安交通大學學報,2011,45(7):1-4,14.
CHEN Lei, LIN Hong, TAO Wenquan. Molecular dynamics simulation of temperature effect on diffusion process of water and proton in proton exchange membrane[J].Journal of Xi’an Jiaotong University, 2011,45(7):1-4,14.
[7]蘇恒,楊勇,陳蓮芳,等. 壓力和溫度對瓦斯擴散規律的影響研究[J].工礦自動化,2015,41(2):65-67.
SU Heng, YANG Yong, CHEN Lianfang, et al. Research of influence of pressure and temperature on gas diffusion low[J]. Industry and Mine Automation, 2015,41(2):65-67.
[8]王瑞,張寧生,劉曉娟,等. 考慮吸附和擴散的頁巖視滲透率及其與溫度、壓力之關系[J]. 西安石油大學學報(自然科學版),2013,28(2):49-53,83,3.
WANG Rui, ZHANG Ningsheng, LIU Xiaojuan, et al. Apparent permeability of shale considering the adsorption and diffusion of gas and the effects of temperature and pressure on it[J]. Journal of Xi’an ShiyouUniversity: Natural Science Edition, 2013,28(2):49-53,83,3
[9]劉炎杰,范延昌,蘇恒. 不同壓力、煤階對煤中甲烷的擴散影響實驗研究[J].煤,2015,24(5):8-11.
LIU Yanjie, FAN Yanchang, SU Heng. Experimental study on methane adsorption and diffusion in different pressure and rank coals[J]. Coal, 2015,24(5):8-11.
[10]劉中民,鄭祿彬,陳國權,等 與濃度相關的擴散系數D_t的求取[J].中國科學(B輯 化學 生命科學 地學),1995,25(7):704-709.
LIU Zhongmin, ZHENG Lubin, CHEN Guoquan, et al. Search of diffusion coefficient Dtrelated with concentration[J]. Science in China: Series B, 1995,25(7): 704-709.
[11]Ogawa K, Inagaki Y. The apparent counter diffusion coefficient of water absorbing on zeolite particles in the case of the water moving through macro-size pores in a column packed with zeolite particles[J]. Chemical Engineering Journal, 2016, 306: 889-896.
[12]Staib G, Sakurovs R, Gray E M A. A pressure and concentration dependence of CO2diffusion in two Australian bituminous coals[J]. International Journal of Coal Geology, 2013, 116: 106-116.
[13]Civan F, Rai C S, Sondergeld C H. Shale-gas permeability and diffusivity inferred by improved formulation of relevant retention and transport mechanisms[J]. Transport in Porous Media, 2011, 86(3): 925-944.
[14]Frenkel D, Smit B. Understanding molecular simulations: from algorithms to applications[J]. Academic, San Diego, 1996.
[15]孫煒,黃素逸,王存文,等. 超臨界水密度和自擴散系數預測的分子動力學模擬[J]. 華中科技大學學報(自然科學版),2008,36(5):103-105.
SUN Wei, HUANG Suyi, WANG Cunwen ,et al. Numeral simulation of the densities and self-diffusion coefficients of supercritical water by molecular dynamics method[J]. Journal of Huazhong University of Science and Technology: Natural Science Edition, 2008, 36(5):103-105.
[16]唐書恒, 張靜平, 吳敏杰. 腐泥煤孔隙結構特征研究[J]. 天然氣地球科學, 2013, 24(2): 247-251.
TANG Shuheng, ZHANG Jingping, WU Minjie. The pore structure characteristic about the sapropelic coal[J]. Natural Gas Geoscience, 2013, 24(2): 247-251.
[17]降文萍, 張群, 姜在炳, 等. 構造煤孔隙結構對煤層氣產氣特征的影響[J]. 天然氣地球科學, 2016, 27(1): 173-179.
JIANG Wenping, ZHANG Qun, JIANG Zaibing, et al. Effect on CBM drainage characteristics of pore structure of tectonic coal[J]. Natural Gas Geoscience, 2016, 27(1): 173-179.

