地面輸油管道泄漏流散數值模擬*

史曉蒙，呂宇玲，2，3，楊玉婷

(1.中國石油大學(華東) 儲運與建筑工程學院，山東 青島 266580;2.山東省油氣儲運安全省級重點實驗室，山東 青島 266580;3.青島市環海油氣儲運技術重點實驗室，山東 青島 266580)

0　引言

隨著大型油庫數量越來越多，儲罐和輸油管道受到腐蝕、高壓及外力破壞等作用，庫區泄漏事故時有發生[1-2]。由于這種泄漏事故泄漏量大，波及范圍廣及原油流散行為的不可預見性，易造成巨大的人員及財產損失。因此研究外泄原油的流散規律對于庫區安全有重要意義。

國內外關于原油泄漏后果的研究有很多。劉瑞凱[3]利用數值模擬研究了海底輸油管道泄漏原油在海泥中的分布。姚志強[4]利用數值模擬確定埋地原油管道發生泄漏時，不同時刻油品在土壤中的擴散范圍。李晰睿[5]以“11·22”中石化東黃輸油管道泄漏爆炸事故為案例，研究了暗渠內輸油管道泄漏、油品蒸發和爆炸過程。國內外學者關于液池擴展面積的計算方法及擴展狀態進行了研究。William[6]和Cronin[7]利用大型實驗研究了儲罐發生破裂時液體對防火堤的沖擊載荷及液池的擴展過程。Brambilla[8]提出了一種應用幾何計算獲得不同阻擋形式下液體擴散最大距離的方法。項小強等[9]采用經驗公式計算液池擴展半徑。王超等[10]提出了一種計算連續泄漏、泄漏停止時液池半徑的半經驗關系式，但由于忽略了液體粘度的影響，該方程不適用于高粘度液體在地面上的蔓延。李大全等[11]建立了一種可以評價泄漏事故危害程度的理論分析模型。潘旭海等[12-13]根據質量守恒定律，建立了動態液池蒸發模型，并用其對苯泄漏事故進行了模擬分析。

上述計算模型大都假設液池為圓柱體，擴展是軸對稱的，這與實際情況不符，因為液體的流散由于受到障礙物阻擋、地形起伏等原因會呈現不規則的形狀。Hirt[14]提出了用VOF方法來模擬動態的自由液面流動，得到不同時刻的相分布圖，并與實驗相吻合。以下主要通過建立庫區地面輸油管道泄漏擴散過程的三維CFD模型，應用FLUENT軟件中的VOF模型進行模擬，分析油品泄漏后擴散趨勢，研究結果有助于分析泄漏事故后果影響范圍，合理制定防護及救援措施。

1　泄漏擴散模型

1.1　數學模型

由于流動主要屬于自由泄流，近似為不可壓縮流體。在空間直角坐標系下采用標準κ-ε湍流模型進行三維數值模擬，控制方程如下。

連續性方程：

(1)

動量方程：

(2)

ε方程：

(3)

κ方程：

(4)

式中：ρ為密度；U為速度矢量；ui為流體沿xi方向的速度分量(xi在三維情況下為x，y，z方向)；η為流體的動力粘度；σε，σκ分別為湍動能和湍動能耗散率所對應的Prandlf數；C1，C2為經驗常數；t為時間。

VOF方法的原理是：在歐拉網格系統上定義一個體積分數函數f，每個網格上的f值由網格內含指定項的體積量來確定，由下列方程確定：

(5)

1.2　模型驗證

選取Cronin & Evans[7]2001年進行的液體在陸地上擴散實驗作為模型驗證的依據。實驗條件為：1個下端有25 mm裂口，高為1.8 m的水槽來模擬直徑為70 m的儲罐破裂，在混凝土表面設置多個阻力探測器監測記錄水波到達時間及傳播速度。基于以上實驗，建立模型，以水作為計算流體，使用VOF模型和標準κ-ε湍流模型，模擬不同地面粗糙度情況下水在地面上的擴展，水泥混凝土面層粗糙度不大于1.0 mm，因此設置粗糙度分別為0，0.1，0.2，0.8 mm，計算結果與實驗結果進行比較，如圖1、圖2所示。

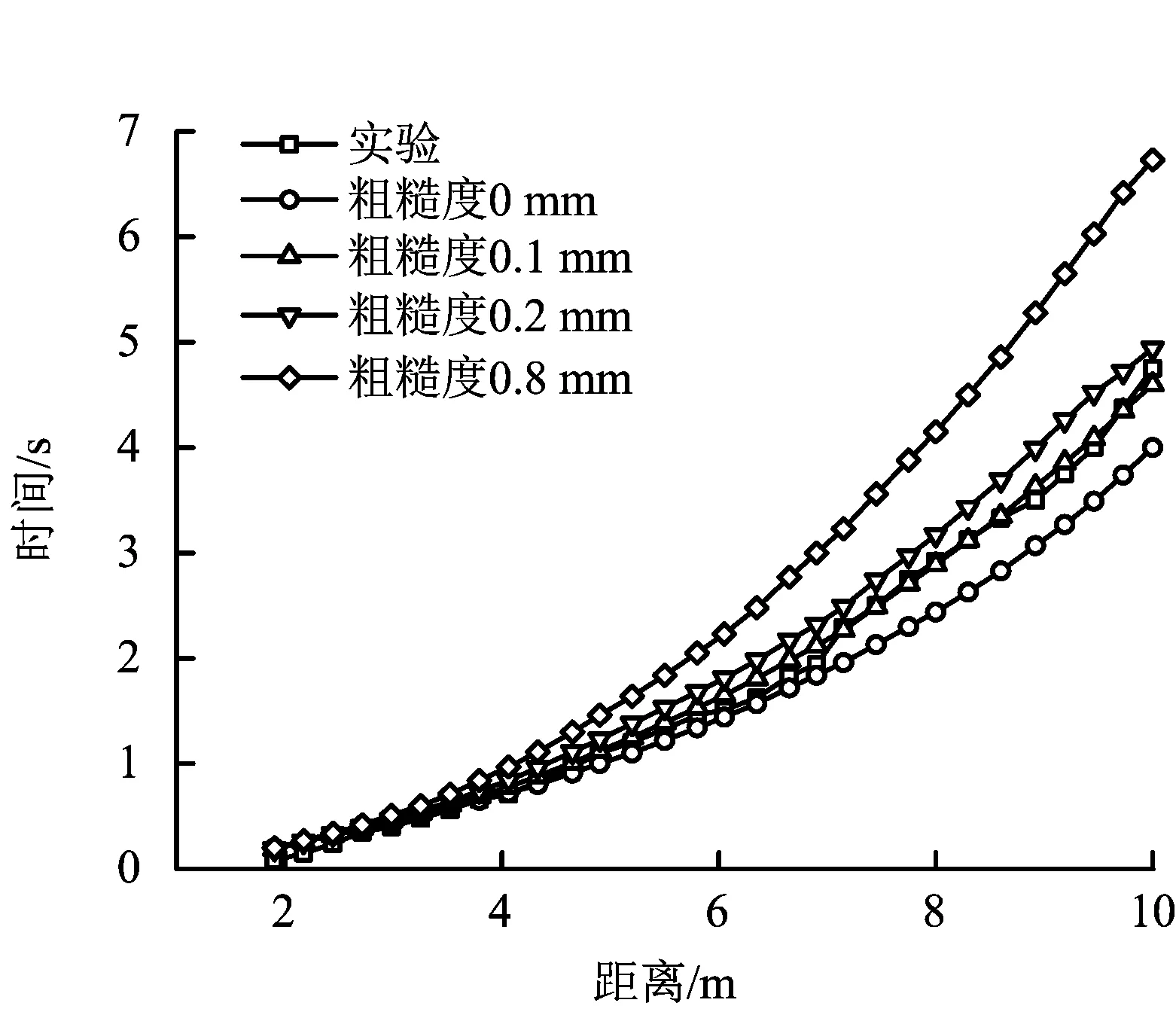
圖1　不同粗糙度下流散時間隨距離變化Fig.1　Dispersion time varies with distance under different roughness

圖2　水波沿中軸線傳播速度隨距離變化Fig.2　Frontal speed along a radial line varies with distance

當地面粗糙度為0.1 mm時，水波前鋒位置隨時間變化以及距泄漏口不同距離的水波傳播速度與實驗數據吻合地較好。因此，采用上文提出的液體流散模型是適用的。

1.3　幾何模型與網格劃分

根據石油庫區消防安全要求，相鄰罐組防火堤腳線之間寬度不小于7 m，故選擇計算區域為60 m×10 m×3 m，內徑為712 mm，考慮到管道外的保溫層厚度，管道離地面高度為0.2 m[15]，在中心處有直徑不同的圓形開孔，模擬接近地面敷設的站內管道發生破裂，模型幾何尺寸如圖3所示。網格采用四面體網格、六面體網格和結構化網格非均勻劃分方法，對泄漏孔口處和地面進行網格加密。

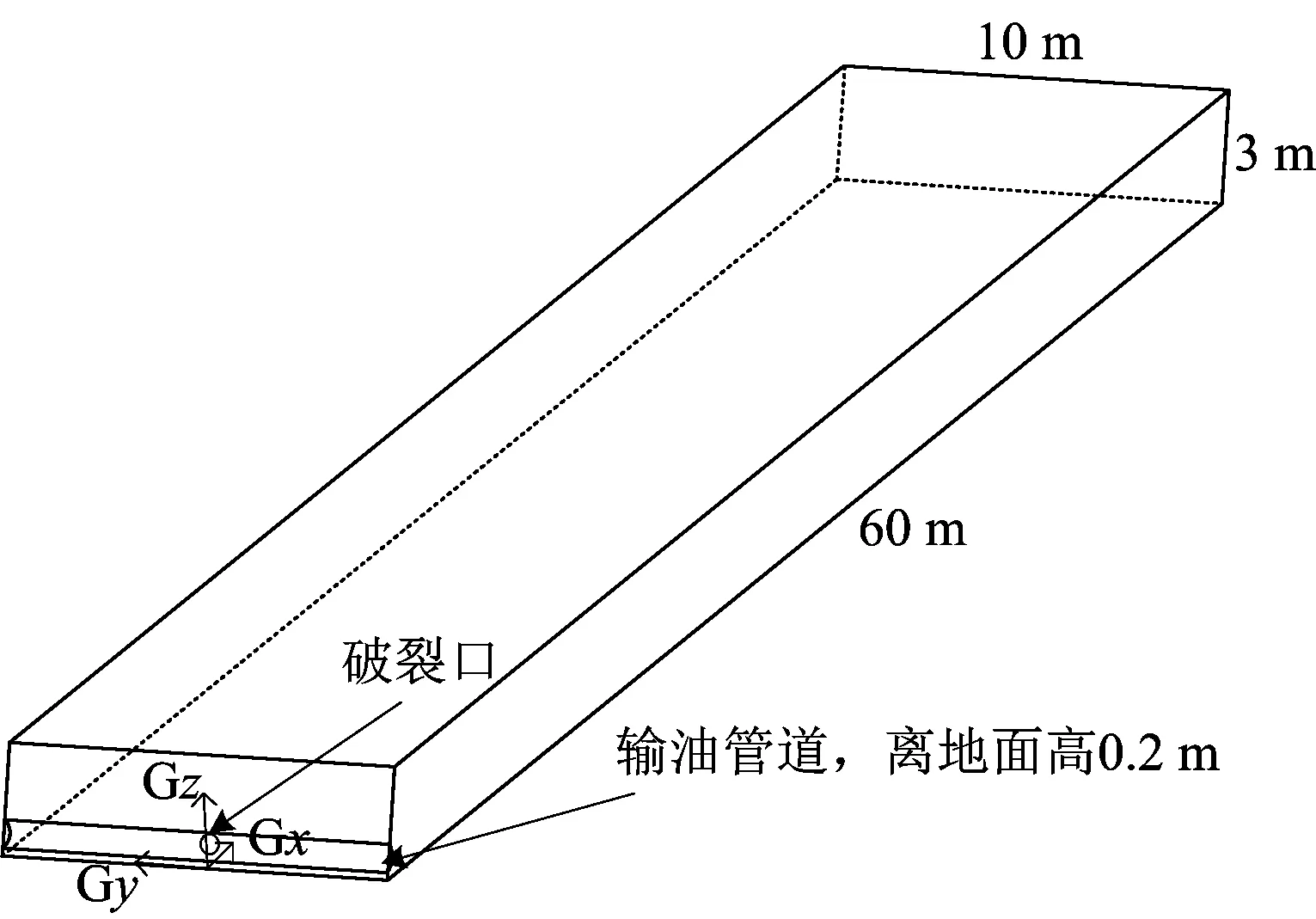
圖3　模型幾何結構尺寸Fig.3　Geometric dimensions of the model

設置管道兩端為壓力入口，油庫內輸油管道運行壓力一般在0.2～0.4 MPa之間，模擬管道壓力分別為0.2，0.25，0.3，0.35，0.4 MPa。設置大氣出口為壓力出口，地面粗糙度為0.000 1 m，油品密度為846.47 kg/m3，粘度為3.458×10-6m2/s。

為了說明網格密度對數值計算結構的影響，對模型

進行疏密2種形式的網格劃分(網格單元數分別為1 560 000和3 300 000)，計算結果相近。計算表明，網格具有一定的無關性，本文使用網格單元數為1 560 000的網格進行計算。

2　油品泄漏規律分析

2.1　管道運行壓力不同的情況下的油品擴散

當泄漏孔口直徑d=0.5 m，管道運行壓力在0.2～0.4 MPa時，油品從破裂口泄漏，即薄壁孔口自由出流，由薄壁圓形孔口泄流公式[16]計算的5種管道運行壓力下泄流噴射速度分別為：21.08，23.57，25.82，28.22，29.82 m/s，本文CFD模擬的速度分別為21.90，23.04，26.76，28.82，29.74 m/s，二者誤差均不超過4%，再次驗證此模型可以用于模擬管道破裂油品泄漏。

模擬得到油品相分布如圖4所示，圖中空白區域表示油品體積分數小于0.05%，代表油品未擴散到的地面，灰色區域表示油品擴散到的地面。

圖4　壓力不同時管道泄漏油品擴散區域變化Fig.4　Affected area under different operating pressure of the pipeline

泄漏油品流散距離隨時間變化關系如圖5所示。流散距離隨時間變化過程可以分為2個階段，第一階段是油品從孔口泄漏，形成紊動射流，油品的擴散受到孔口射流的沖擊影響，流散距離隨著時間呈指數增長，由于受到地面摩擦阻力的作用，流散速度逐漸減小。第二個階段認為射流過程結束，不再考慮射流作用，同時橫向擴散受到阻擋，液體在地面摩擦力和液體表面張力的作用下擴展，擴展速度保持不變。流散距離隨時間變化呈現線性函數增長趨勢，其曲線斜率表示油品在地面擴展的速度。隨著壓力的增大，擴展速度增大。可以將流散0～5 s作為第一階段，5 s之后作為第二階段。

2.2　管道泄漏口面積不同時油品擴散

不同泄漏孔直徑油品擴散區域變化如圖6所示，管道泄漏面積的變化對油品的橫向擴散影響較為明顯。當泄漏口直徑d=0.3 m時，泄漏油品從泄漏口呈直線噴射出，橫向擴展較小，液體集中在射流軸線上向前推進，在短時間內流散距離最遠。當d=0.5 m時，泄漏口附近油品呈扇形噴射，在中心線上的流散前鋒也在迅速向前推進的同時，液體也發生橫向擴展。

油品擴散距離隨不同管道破裂孔徑的變化如圖7所示，當d=0.5 m時，由于泄漏口附近液體橫向速度較大，油品橫向擴展最遠，液體厚度變薄，向前擴展受到影響，流散距離較小。當流散不受到射流的影響時，油品擴展速度隨泄漏孔直徑增大而增大。

圖5　不同管道壓力下泄漏流散距離與時間的變化關系Fig.5　Spread distance vs. spread time under different operating pressure of the pipeline

2.3　擴展速率與泄漏量的關系

由2.2節和2.1節分析得到，當液體擴散不受射流影響擴展速度穩定時，擴展速度隨壓力增大而增大，隨泄漏孔徑增大而增大，擴展速度跟泄漏流量有一定關系，如圖8所示。隨著泄漏流量增大，擴展速度增大，擴展速度可以表示為關于泄漏流量的函數：

v=1.869 61+0.084 54e0.493 28Q

(6)

式中：Q為泄漏流量，m3/s。

圖6　不同泄漏孔直徑油品擴散區域變化Fig.6　Affected area under different leakage hole diameter

圖7　不同泄漏口直徑流散距離隨泄漏時間的變化關系Fig.7　Spread distance vs. spread time under different leakage hole diameter

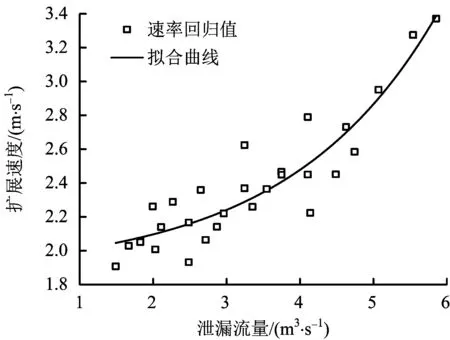
圖8　擴展速度與泄漏流量的關系Fig.8　Spread velocity vs. leakage flow rate

3　流散面積模型

假定在此種泄漏流散環境下，油品流散面積隨管道壓力、泄漏孔徑和流散時間變化的關系為S=f(p,d,t)。

3.1　流散面積隨管道壓力的變化

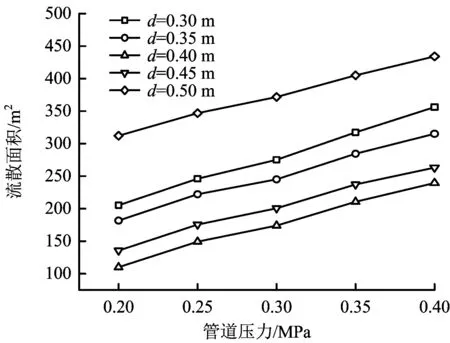
圖9　8 s時流散面積隨管道壓力的變化Fig.9　Affected area vs. operating pressure at t=8 s

(7)

式中：d為泄漏孔直徑，m。

圖10　壓力相關系數隨泄漏孔徑的變化Fig.10　Coefficient of operating pressure vs. the leakage hole diameter

3.2　流散面積隨破裂孔徑的變化

圖11是各個管道壓力下泄漏8 s時流散面積隨泄漏孔徑的變化關系，可以回歸成流散面積S關于泄漏孔徑d的一元三次方程：

y=A+Bx+Cx2+Dx3

(8)

(9)

式中:p為管道壓力，MPa。

圖11　8 s時流散面積隨泄漏孔徑的變化Fig.11　Affected area vs. the leakage hole diameter at t=8 s

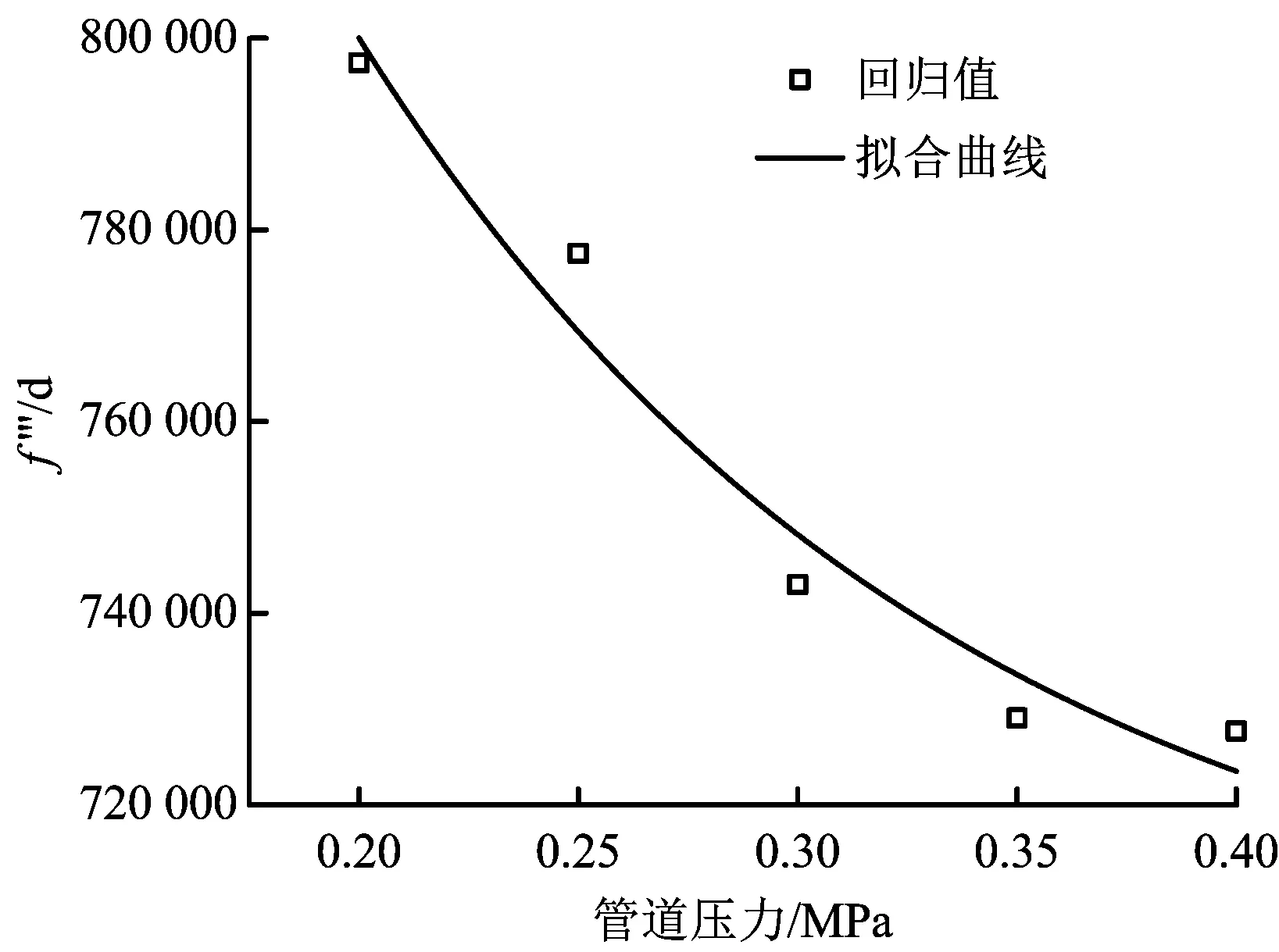
圖12　泄漏孔徑系數與管道壓力的變化Fig.12　Coefficient of leakage hole diameter vs. the operating pressure

3.3　流散面積隨泄漏時間的變化

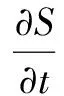
(10)

圖13　泄漏孔徑為0.5 m時流散面積隨時間的變化Fig.13　The affected area vs. time at d=0.5 m

圖14　時間相關系數與管道壓力的關系Fig.14　Coefficient of time vs. the operating pressure

3.4　擴展速率方程式和流散面積模型的驗證

假設工況1：管道壓力0.32 MPa，泄漏孔直徑為0.4 m；假設工況2：管道壓力為0.3 MPa，泄漏孔直徑為0.38 m。使用得到的偏微分方程和數值模擬對2種假設工況分別進行計算，并對結果進行比較。以式(6)得到油品穩定擴展速率分別為2.31，2.22 m/s，利用數值模擬得到油品穩定擴展速率分別為2.39，2.19 m/s；使用式(7)，(8)，(9)得到的油品擴散面積分別為189.46，201.67 m2，利用數值模擬得到油品擴散面積分別為187.35，209.58 m2。二者相差不大，說明上文擴展速率方程式和流散面積模型在一定范圍內具有適用性。

4　結論

1)若管道發生泄漏，在寬度為10 m的地面上擴散，當擴散速度穩定時，穩定的擴展速度隨泄漏流量增大而增大，擴展速度與泄漏量的具體關系為：

v=1.869 61+0.084 54e0.493 28Q

(11)

2)在寬度為10 m的流散區域內，管道壓力為0.2～0.4 MPa，泄漏孔徑為0.3～0.5 m時，表示流散面積S與管道壓力p、泄漏孔徑d、泄漏時間t關系的偏微分方程組為：

(12)

當泄漏孔直徑相同時，流散面積隨管道壓力增大呈線性函數增大，壓力相關系數與泄漏孔徑呈指數函數關系；當管道壓力相同時，流散面積隨泄漏孔徑呈三次函數變化，先減小后增大，泄漏孔徑相關系數與管道壓力呈指數函數關系；在泄漏的開始階段，流散面積隨泄漏時間的變化隨管道壓力呈線性增長。

[1]Chang J I, Lin C C. A study of storage tank accidents [J]. Journal of Loss Prevention in the Process Industries, 2006, 19(1):51-59.

[2]潘旭海, 蔣軍成. 重(特)大泄露事故統計分析及事故模式研究[J]. 化學工業與工程, 2002, 19(3):248-264.

PAN Xuhai, JIANG Juncheng. Analysis on important release accidents and modes studying [J].Chemical Industry and Engineering, 2002, 19(3):248-264.

[3]劉瑞凱，吳明，王同秀，等. 海底埋地熱油管道泄漏擴散的數值模擬[J]. 中國安全生產科學技術, 2012, 8(8):63-68.

LIU Ruikai, WU Ming, WANG Tongxiu, et al. Numerical simulation on leakage and diffusion of submarine buried hot oil pipeline[J]. Journal of Safety Science and Technology, 2012, 8(8):63-68.

[4]姚志強,埋地原油管道油品泄漏擴散三維數值模擬[J]. 中國安全生產科學技術, 2015, 11(6):132-136.

YAO Zhiqiang，Three-dimensional numerical simulation on leakage and diffusion of oil in buried crude oil pipeline[J]. Journal of Safety Science And Technology, 2015,11(6):132-136.

[5]李晰睿. 暗渠下輸油管道泄漏爆炸分析及事故后果研究[D]. 成都：西南石油大學, 2015.

[6]An experimental investigation of bund wall overtopping and dynamic pressures on the bund wall following catastrophic failure of a storage vessel[M]. HSE Books, 2005:4-42.

[7]CLEAVER R P, CRONIN P S, EVANS J A, et al. An experimental study of spreading liquid pools[C]//Proceedings of the Hazards XVI. Manchester, UK, 2001：167-179.

[8]Brambilla S, Manca D. On pool spreading around tanks: Geometrical considerations [J]. Journal of Hazardous Materials, 2008, 158(1): 88-99.

[9]項小強, 戴聯雙, 曹濤，等. 輸油管道泄漏液池的蒸氣云擴散模型[J]. 油氣儲運, 2011, 30(5): 334-336.

XIANG Xiaoqiang, DAI Lianshuang, CAO Tao，et al. Vapor cloud diffusion model for leakage pool of oil pipeline [J]. Oil and Gas Storage and Transportation, 2011, 30(5): 334-336.

[10]王超. 液體泄漏形成液池擴展面積的計算方法綜述[J]. 安全與環境工程, 2012, 19(6):125-128.

WANG Chao. Review of area expansion calculation method for liquid leakage to liquid pool [J]. Safety and Environmental Engineering, 2012，19(6)：125-128.

[11]李大全, 姚安林. 成品油管道泄漏擴散規律分析[J]. 油氣儲運, 2006, 25(8):18-24.

LI Daquan, YAO Anlin. Analysis of leakage and diffusion law of oil product pipeline [J]. Oil and Gas Storage and Transportation, 2006, 25(8):18-24.

[12]潘旭海, 蔣軍成. 泄漏液池動態蒸發過程模型研究與分析[J]. 工業安全與環保, 2006, 32(4):43-46.

PAN Xuhai, JIANG Juncheng. Research and analysis on model for dynamic evaporation process of pool [J]. Industrial Safety and Environmental Protection,2006, 32(4):43-46.

[13]潘旭海, 蔣軍成. 危險品罐區突發性泄漏事故實時環境風險模擬分析[J]. 環境科學學報, 2004, 24(3):539-544.

PAN Xuhai, JIANG Juncheng. Real-time environment risk analysis for accident release of hazardous materials around tank area [J]. Acta Scientiae Circumstantiae, 2004, 24(3):539-544.

[14]Hirt C W, Nichols B D. Volume of fluid (VOF) method for the dynamics of free boundaries[J]. Journal of Computational Physics, 1981, 39(1): 201-225.

[15]樊寶德, 朱煥勤. 油庫設計規范[M].北京：中國石化出版社, 2007: 109-115.

[16]倪玲英. 工程流體力學[M]. 東營：中國石油大學出版社，2012：212-215.