一題變多題，一點引一面
——試論高中數(shù)學(xué)教學(xué)中的引深藝術(shù)

江蘇省揚州市仙城中學(xué)(225200)

桂 佳●

一題變多題，一點引一面
——試論高中數(shù)學(xué)教學(xué)中的引深藝術(shù)

江蘇省揚州市仙城中學(xué)(225200)

桂 佳●

高中階段的數(shù)學(xué)知識相互關(guān)聯(lián)，呈輻射狀呈現(xiàn).為此，教學(xué)活動不能浮于表面，而是要從深層次入手，由點及面，從基礎(chǔ)向靈活引深.作者結(jié)合教學(xué)理論與實踐經(jīng)驗，以幾個典型知識模塊為代表，對引深教學(xué)的方法進行了闡述.

高中；數(shù)學(xué)；引深

在平日的教學(xué)過程中，作者經(jīng)常會以“森林”來比喻高中數(shù)學(xué)這門學(xué)科.在這片知識的森林當中，樹木的種類、數(shù)量眾多，更重要的是，向森林的深處走去，總能看到隱藏著的新風(fēng)景.同樣地，對于高中數(shù)學(xué)來講，僅從表面來看待知識內(nèi)容的形態(tài)是遠遠不夠的，我們還需要從基礎(chǔ)知識出發(fā)繼續(xù)引深，去努力發(fā)現(xiàn)更深層次的知識與方法.這是數(shù)學(xué)學(xué)習(xí)的樂趣，更是數(shù)學(xué)教學(xué)的藝術(shù).

一、從函數(shù)角度引深，拓展思維平面

函數(shù)知識在整個數(shù)學(xué)教學(xué)過程當中都是貫穿始終的，自然也是高中階段的教學(xué)重點.我們不僅要將函數(shù)作為一個具體知識點來處理，更要將之視為一種思維方法，滲透到學(xué)生們的思維意識當中去.在這之中，知識的引深就顯得頗為重要了.

例如，在對函數(shù)的基本性質(zhì)進行教學(xué)時，我先向?qū)W生們提出了這樣一個問題：有一個函數(shù)f(x)，它是一個偶函數(shù)，且在(0，+∞)上單調(diào)遞減.那么，這個函數(shù)在(-∞，0)上是單調(diào)遞增的還是單調(diào)遞減的呢？請對判斷結(jié)論給出相應(yīng)證明.掌握了基本知識后，這個問題的解決難度并不算大.緊接著，我又對問題進行了變式：現(xiàn)有如下四個函數(shù)：(1)y=-x3，x∈R；(2)y=sinx，x∈R；(3)y=x，x∈R；(4)y=0.5x，x∈R，在這之中，哪個函數(shù)在其定義域之內(nèi)既是減函數(shù)，又是奇函數(shù)呢？隨后，我又繼續(xù)提問：若偶函數(shù)y=f(x)在(-∞，0]上單調(diào)遞增，且f(a)≤f(2)，則實數(shù)a的取值范圍如何？隨著上述問題的不斷變化引深，學(xué)生們對于函數(shù)奇偶性與單調(diào)性之間的關(guān)系了解得愈發(fā)清晰細致了.

函數(shù)知識的廣泛適用特征決定了教師們在對這部分內(nèi)容進行引深時，并不需要僅僅局限于函數(shù)的知識模塊中.只要是涉及到函數(shù)方法進行處理的內(nèi)容，都可以稍稍停下腳步，進行靈活拓展.它的效果將會在數(shù)學(xué)學(xué)習(xí)的各個側(cè)面得到展現(xiàn).

二、從三角角度引深，拓展思維平面

對于高中數(shù)學(xué)來講，三角知識是一個具有雙重屬性的內(nèi)容.從代數(shù)角度來看，三角知識中具有靈活的計算推導(dǎo)元素，是代數(shù)能力考查的重點.從幾何角度來看，三角知識的呈現(xiàn)往往伴隨著幾何圖形的出現(xiàn)，要求學(xué)生們對于三角形中的線段與角度之間的關(guān)系也要掌握到位.這也意味著，三角知識成為了靈活引深教學(xué)的重點對象.

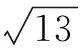
鑒于三角知識中所反映出的代數(shù)與幾何的雙重屬性，教師們在對這部分內(nèi)容進行引深拓展時，也就擁有了更多選擇的空間.只有將上述兩個方面的元素都涵蓋到位，才能夠引導(dǎo)學(xué)生們將三角模塊的知識方法理解透徹.

三、從數(shù)列角度引深，拓展思維平面

從高中數(shù)學(xué)各類綜合測驗的分值比例來看，數(shù)列絕不是占有比重最大的，但知識難度卻是能夠排在前列的.很多學(xué)生也表示，數(shù)列知識雖然看似簡單清晰，真正解題時卻總是找不到準確的分析路徑.因此，為了實現(xiàn)學(xué)生數(shù)學(xué)能力的協(xié)同提升，對于數(shù)列知識的有效教學(xué)必須得到重視.

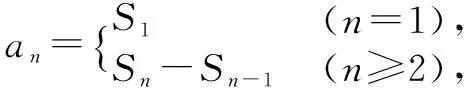
從基礎(chǔ)知識的角度來看，數(shù)列模塊中的公式、定理數(shù)量并不是最多的，表達起來也并不是那么模糊繁瑣，但到了具體問題的解答當中，卻可以變化出各種形態(tài).這就說明，每一個基本知識點都是可以向多個角度進行拓展的.抓住了這一點，教學(xué)引深也就有方向了.

引深的過程是知識能力的延長，也是一種變化.為了實現(xiàn)教學(xué)引深的理想效果，學(xué)生們的思維必須先活躍起來，方能在這個變化的過程中游刃有余.通過上述變式習(xí)題的運用，學(xué)生們的思維熱度持續(xù)增高，并順利地在基礎(chǔ)內(nèi)容之外看到了更多拓展空間，隨著不斷探索看到了數(shù)學(xué)知識的全貌.一題變多題的方法，成功地從一個知識點擴展出了一個知識面，教學(xué)優(yōu)化效果顯著.

[1]吳志勇.高中數(shù)學(xué)探究型復(fù)習(xí)課的樣式及實踐 [J]. 中學(xué)課程輔導(dǎo)(教師通訊)，2015(20)

G632

B

1008-0333(2017)09-0026-01