逆用求導法則 合理構(gòu)造函數(shù)

逆用求導法則 合理構(gòu)造函數(shù)

■湖北省武漢市黃陂區(qū)第六中學 梅 磊

構(gòu)造函數(shù)求解不等式問題是一類極富思考性和挑戰(zhàn)性、具有相當深度和難度的重要題型,備受各類考試命題者的青睞,頻頻出現(xiàn)在各類考試試卷中,它是考查同學們數(shù)學能力和素養(yǎng)的極好素材。解決此類問題的關鍵在于逆用求導法則,合理構(gòu)造函數(shù),下面通過幾道例題說明常見的構(gòu)造函數(shù)的類型與方法。

1.利用和差函數(shù)求導法則構(gòu)造函數(shù)

(1)對于不等式f'(x)+g'(x)＞0,構(gòu)造函數(shù)F(x)=f(x)+g(x)。

(2)對于不等式f'(x)-g'(x)＞0,構(gòu)造函數(shù)F(x)=f(x)-g(x)。

特別地,對于不等式f'(x)＞k(k≠0),構(gòu)造函數(shù)F(x)=f(x)-k x。(2 0 1 5年福建卷理科第1 0題)設定義在R上的函數(shù)f(x)滿足f(0)=-1,其導函數(shù)為f'(x)滿足f'(x)＞k＞1,則下列結(jié)論中一定錯誤的是( )。

解析：設F(x)=f(x)-k x,則F'(x)= f'(x)-k＞0,所以F(x)在R上單調(diào)遞增。

2.利用積商函數(shù)求導法則構(gòu)造函數(shù)

(3)不等式f'(x)g(x)+f(x)g'(x)＞0,可構(gòu)造函數(shù)F(x)=f(x)g(x)。

(4)不等式f'(x)g(x)-f(x)g'(x)＞ 0,可構(gòu)造函數(shù)F(x

(2 0 0 4年高考湖南卷理科第1 2題)設f(x),g(x)分別是定義在R上的奇函數(shù)和偶函數(shù)。當x＜0時,f'(x)g(x)+ f(x)g'(x)＞0,且g(-3)=0。則不等式f(x)g(x)＜0的解集是( )。

A.(-3,0)∪(3,+∞)

B.(-3,0)∪(0,3)

C.(-∞,-3)∪(3,+∞)

D.(-∞,-3)∪(0,3)

解析：設F(x)=f(x)g(x),易知F(x)為奇函數(shù)。

由x＜0時,F'(x)＞0且F(-3)=0,得F(x)在(-∞,0)和(0,+∞)上為增函數(shù),且F(3)=-F(-3)=0。

所以不等式F(x)=f(x)g(x)＜0的解集為(-∞,-3)∪(0,3),選D。

上述(3)(4)都是利用積商函數(shù)求導法則的一般情況,但在考試中,g(x)往往是具體函數(shù),所以還有一些常見的利用積商函數(shù)求導法則的特殊情況,如下面(5)～(2 2)。

(5)對于不等式x f'(x)+f(x)＞0,構(gòu)造函數(shù)F(x)=x f(x)。

(6)對于不等式x f'(x)-f(x)＞0,構(gòu)造函數(shù)F(x

(2 0 1 5年全國Ⅱ卷理科第1 2題)設函數(shù)f'(x)是奇函數(shù)f(x)(x∈R)的導函數(shù),f(-1)=0,當x＞0時,x f'(x)-f(x)＜0,則使得f(x)＞0成立的x的取值范圍是( )。

A.(-∞,-1)∪(0,1)

B.(-1,0)∪(1,+∞)

C.(-∞,-1)∪(-1,0)

D.(0,1)∪(1,+∞)

(7)對于不等式x f'(x)+n f(x)＞0,構(gòu)造函數(shù)F(x)=xnf(x)。

(8)對于不等式x f'(x)-n f(x)＞0,構(gòu)造函數(shù)(2 0 0 9年高考天津卷文科第1 0題)設函數(shù)f(x)在R上的導函數(shù)為f'(x), 2f(x)+x f'(x)＞x2,下面的不等式在R上恒成立的是( )。

A.f(x)＞0 B.f(x)＜0

C.f(x)＞x D.f(x)＜x

解析：設F(x)=x2f(x),則F'(x)= 2x f(x)+x2f'(x)=x[2f(x)+x f'(x)]。

當x=0時,由2f(0)+0f'(0)＞02=0,得f(0)＞0。

當x＞0時,2f(x)+x f'(x)＞x2＞0, F'(x)＞0,F(x)單調(diào)遞增。從而F(x)＞F(0)=0,即x2f(x)＞0,故f(x)＞0。

當x＜0時,2f(x)+x f'(x)＞x2＞0, F'(x)＜0,F(x)單調(diào)遞減。從而F(x)＞F(0)=0,即x2f(x)＞0,故f(x)＞0。

綜上所述,f(x)＞0。選A。

(9)對于不等式f'(x)+f(x)＞0,構(gòu)造函數(shù)F(x)=exf(x)。

(1 0)對于不等式f'(x)-f(x)＞0,構(gòu)造函數(shù)F(x)

設函數(shù)f(x)在R上的導函數(shù)為f'(x),f'(x)+f(x)＞0,則對于任意正數(shù)a,必有( )。

A.f(a)＞eaf(0) B.f(a)＜eaf(0)

解析：設F(x)=exf(x),則F'(x)=,所以F(x)在R上單調(diào)遞增。

又a＞0,所以F(a)＞F(0),即eaf(a)＞e0f(0),所以選D。

(1 1)對于不等式f'(x)+k f(x)＞0,構(gòu)造函數(shù)F(x)=ekxf(x)。

(1 2)對于不等式f'(x)-k f(x)＞0,構(gòu)造函數(shù)

設函數(shù)f(x)在R上的導函數(shù)為f'(x),2f'(x)＞f(x),則( )。

A.3f(2l n 2)＞2f(2l n 3)

B.3f(2l n 2)＜2f(2l n 3)

C.3f(2l n 2)=2f(2l n 3)

D.3f(2 l n 2)與2f(2 l n 3)的大小不確定

(1 3)對于不等式f'(x)+k x f(x)＞0,構(gòu)造函數(shù)F(x)=exkf(x)。

(1 4)對于不等式f'(x)-k x f(x)＞0,構(gòu)造函數(shù)

設函數(shù)f(x)在R上的導函數(shù)為f'(x),f'(x)＜2x f(x),則( )。

A.e5f(2)＞f(3)

B.e5f(2)＜f(3)

C.e5f(2)=f(3)

A.e5f(2)與f(3)的大小不確定

(1 5)對于不等式f'(x)+l na f(x)＞0,構(gòu)造函數(shù)F(x)=axf(x)。

(1 6)對于不等式f'(x)-l na f(x)＞0,構(gòu)造函數(shù)

設函數(shù)f(x)在R上的導函數(shù)為f'(x),f'(x)＞l n2f(x),則( )。

A.2f(-2)＜f(-1)

B.2f(1)＞f(2)

C.4f(-2)＞f(0)

D.2f(0)＞f(1)

(1 7)對于不等式f(x)+f'(x)t a nx＞0,構(gòu)造函數(shù)F(x)=s i nx f(x)。

(1 8)對于不等式f(x)-f'(x)t a nx＞ 0,構(gòu)造函數(shù)

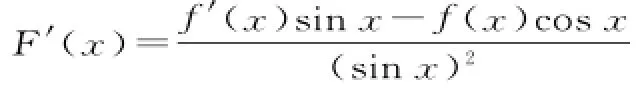
(1 9)對于不等式f'(x)-f(x)t a nx＞0,構(gòu)造函數(shù)F(x)=c o sx f(x)。

(2 0)對于不等式f'(x)+f(x)t a nx＞ 0,構(gòu)造函數(shù)

設f(x)是定義在上的函數(shù),f'(x)是它的導函數(shù),f'(x)＜f(x)· t a nx,則( )。

B.2 c o s1f(1)＞

解析：設F(x)=c o sx f(x),則F'(x)= f'(x)c o sx-f(x)s i nx=c o sx[f'(x)-f(x)t a nx]＜0,F(x)在上單調(diào)遞減。

利用導數(shù)構(gòu)造函數(shù)解不等式問題在各類的考試中常考常新,除上述這些常見的構(gòu)造函數(shù)的類型之外,還會出現(xiàn)其他構(gòu)造函數(shù)的試題。解題的關鍵依然是逆用求導法則,合理構(gòu)造函數(shù),不管哪種構(gòu)造,都需要結(jié)合問題的外形結(jié)構(gòu)特征與求導法則進行合理構(gòu)造,向著有利于判斷函數(shù)單調(diào)性方向構(gòu)造,正所謂“求導誠可貴,構(gòu)造價更高”。

(責任編輯 徐利杰)