數學“四基”的研究現狀及展望

曾 崢，楊豫暉，武金艷

?

數學“四基”的研究現狀及展望

曾 崢1，楊豫暉2，武金艷3

（1．佛山科學技術學院，廣東佛山 528000；2．海南師范大學，海南海口 571158；3．海口市瓊山三小，海南海口 571100）

數學“四基”是近年來中國數學教育研究的重點與熱點問題之一，特別是《義務教育數學課程標準（2011年版）》正式發行后，對數學“四基”的研究更為豐富．以數學“四基”為關鍵詞在中國知網上篩選出相關文獻194篇，這些成果對數學“四基”的研究大致分為：數學“四基”的形成發展研究，數學“四基”內涵研究，數學“四基”關系研究和數學“四基”教學研究等4個方面，對這些研究成果進行結構化梳理和分析，為進一步的研究提供借鑒．

數學“四基”；內涵；關系；教學實踐

《義務教育數學課程標準（2011年版）》（以下簡稱“2011版課標”）指出：通過義務教育階段的數學學習，學生能：獲得適應社會生活和進一步發展所必需的數學的基礎知識、基本技能、基本思想、基本活動經驗[1]，即在“雙基”的基礎上，明確提出“四基”課程目標．2013年6月召開的“未來十年中國數學教育展望”和2014年5月召開的“首屆華人數學教育會議”也安排了數學“四基”的討論專題．由此可見，數學“四基”已成為中國數學教育研究的重點和熱點．相關文獻的研究方向和內容主要涵蓋了數學“四基”的形成發展研究，數學“四基”內涵研究，數學“四基”關系研究和數學“四基”教學研究等4個方面．

1 數學“四基”的形成與發展

數學“四基”是對數學雙基的繼承和發展，與此相關的文獻主要采用歷史法和文獻法進行分析．梳理如下：

1.1 數學雙基的形成與發展概述（1952—2000年）

數學雙基的形成與發展大致經歷了4個階段：

1952年頒布的《中學數學教學大綱（草案）》中首次明確提出“基礎知識”和“技能”要求，“雙基”一詞并未提出[2]．同年頒布的《小學算數教學大綱（草案）》中提出：保證兒童自覺地和鞏固地掌握算術知識和直觀幾何知識，并使他們獲得實際運用這些知識的技能[3]．這是（小學）數學“雙基”的最初形式．

1963—1982年，“雙基”逐步形成，教材和教學體現“雙基”．1978年《全日制十年制學校小學數學教學大綱（試行草案）》，1980年《全日制十年制學校中學數學教學大綱（試行草案）》和1982年《全日制六年制重點中學數學教學大綱（征求意見稿）》都對“雙基”教學的要求逐步細化．該階段的教材扎扎實實地加強了基礎知識和基本訓練，內容比較充實，闡述比較嚴謹、細致，突出了“雙基”[4]．

1986—1988年：明確界定“雙基”，教材和教學強化雙基．1986年，《全日制中小學數學教學大綱》把教學目的界定為“雙基+三大能力+其他”的結構，此后的大綱都沿用了“數學的基礎知識和基本技能”這一表述．1988年《九年制義務教育全日制初級中學數學教學大綱（初審稿）》第一次明確界定了數學雙基教學的含義．

1992—2000年：“雙基”細化，雙基教學異化．該階段的教學大綱主張降低“雙基”的難度，刪除繁、難、偏、舊內容．但是在實際教學中，由于高考競爭加劇和唯分數論思想的泛濫，雙基教學實踐開始過度強調記憶、過度強化訓練，出現“題海戰術”、“應試雙基”等異化現象[2]．

1.2 數學雙基向數學“四基”逐步轉化（2001—2011年）

2001年《全日制義務教育數學課程標準（實驗稿）》（以下簡稱“實驗稿”）把“雙基”的含義明確為：經歷將一些實際問題抽象為數與代數問題的過程，掌握數與代數的基礎知識和基本技能，并能解決簡單的問題……[5]對數學雙基的表述更加細致．

同時，實驗稿在課程總體目標的第一條表述到：通過義務教育階段的數學學習，學生能夠獲得適應未來社會生活和進一步發展所必需的重要數學知識（包括數學事實、數學活動經驗）以及基本的數學思想方法和必要的應用技能．這條目標包含了兩個信息：一是在總體目標的表述中已經包含了重要的數學知識、數學事實、數學活動經驗、基本的數學思想方法和必要的應用技能等提法，雖排列尚不夠清晰，但明確地體現出自20世紀90年代中期以來，以《21世紀中國數學教育展望》為代表的中國數學課程改革的階段性研究成果，以及專為實驗稿研制開展的若干項重大基礎性研究的成果[6]．二是“數學活動經驗”沒有單列，而是作為數學知識的重要組成部分在括號里出現，反映了當時實驗稿研制者們更為關注知識觀的變革，另一方面當時圍繞“活動”積累的“經驗”還不多．由此可見，實驗稿的頒布標志著數學“四基”進入萌芽期．

2004年教育部根據《中共中央國務院關于進一步加強和改進未成年人思想道德建設的若干意見》和教育部關于貫徹這一文件的《實施意見》，開始對實驗稿進行第一次修訂，把總體目標的第一條修改為：通過義務教育階段的數學學習，學生能夠獲得適應未來社會生活和進一步發展所必需的數學知識、數學活動經驗、基本的數學思想方法和必要的應用技能．此次修改把“數學活動經驗”與知識、思想、技能并列，已經形成了“四基”的基本輪廓[6]．但是此次修訂因為種種原因并沒有成功．

2007年4月，在寧波數學教育高級研討班上史寧中教授在題為“《數學課程標準》的若干思考”報告中指出：如果在中國中小學數學教育中，一方面保持“數學‘雙基’教學”這個合理內核，另一方面添加“基本思想”和“基本活動經驗”，出現既有“演繹能力”又有“歸納能力”的培養模式，就必將出現“外國沒有的我們有、外國有的我們也有”的局面，到了那一天，我們就能自豪地說，中國的基礎教育領先于世界[7]．數學“基本思想方法”和“基本活動經驗”再一次被強調．其中，2005年4月20日，教育部就成立了以史寧中教授為組長的《數學課程標準》修訂組．

2011年12月，教育部正式頒布2011版課標，標志著中國數學基礎教育課程目標從重視“雙基”發展為重視“四基”．2011版課標對“四基”進行了完整、清晰、準確的描述：通過義務教育階段的數學學習，學生能獲得適應社會生活和進一步發展所必需的數學的基礎知識、基本技能、基本思想、基本活動經驗[1]．

2 數學“四基”的內涵

基礎知識和基本技能是從數學雙基中繼承下來的，在數學“四基”的背景下基礎知識的內涵雖然發生了一些細微變化，但對其內涵界定學術界持統一觀點，把基礎知識界定為：數學中的基本概念、基本性質、基本法則、基本公式、基本定律和基本定理等．把基本技能界定為：按照一定的程序與步驟進行運算、推理、作圖、處理數據等心智活動方式[8]．

基本思想和基本活動經驗是對數學雙基的發展，在課標修訂版中并沒有明確說明什么是數學基本思想、數學思想有哪些，什么是數學基本活動經驗．表1列舉了幾種目前國內對基本思想和基本活動經驗的認識和看法．

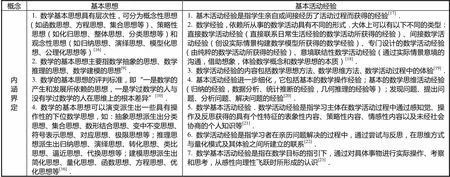
表1 基本數學思想和基本數學活動經驗的內涵

目前國內公認的數學基本思想主要有3大類：數學抽象的思想、數學推理的思想和數學建模的思想．對數學基本活動經驗雖然還沒有形成共識，但有幾點是共同的：

第一，基本活動經驗是在特定的數學活動中積累的．這些活動必須有明確的數學內涵和數學目的，體現數學的本質；第二，基本活動經驗是一種組合體，包括了數學活動中的主觀體驗以及獲得的客觀認識；包括數學活動的結果，更包括活動的過程；第三，數學活動經驗的類型目前還沒有統一，但其核心應該是如何思考的經驗，促進學生學會運用數學的思維方式進行思考；第四，數學活動經驗最終可以幫助學生建立自己的數學現實和數學學習的直覺，這種直覺一旦生成，那么在后續的學習和問題解決中將起到重要作用；第五，基本活動經驗的積累，大致需要經過“經歷、內化、概括、遷移”的過程[24]．

3 數學“四基”的相關關系探討

數學“四基”的關系可分為數學“四基”的內部關系和數學“四基”的外部關系．

3.1 數學“四基”的內部關系

對于數學“四基”的內部關系主要有以下幾種認識：

（1）“基礎知識、基本技能”是顯性目標，而“基本思想、基本活動經驗”是隱性目標[25]．

“四基”的基本形式是一個三維模塊，學生頭腦里的數學大廈，是在一個個的基礎模塊之上建立起來的．數學基本知識的積累過程、基本技能的演練過程和基本數學思想方法的形成過程形成了3個維度，基本數學活動經驗本身并不構成一個單獨的維度，而是填充在三維模塊中間的粘合劑．學生通過無處不在的基本數學活動獲得的經驗，與數學基本知識、基本技能、基本思想方法交織在一起，滲透在整體數學學習過程中，如圖1所示[26]．

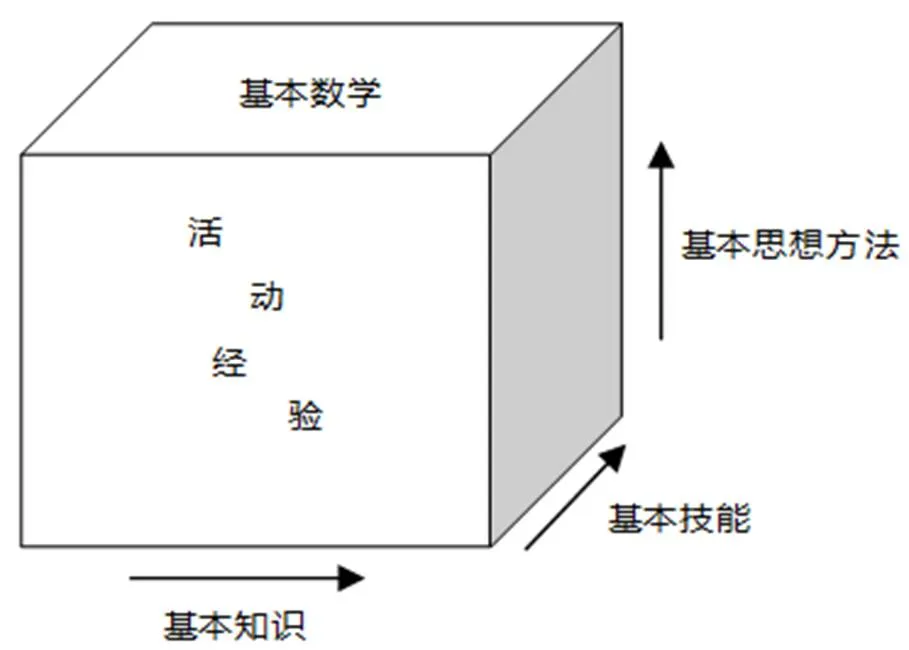
圖1 四基模塊示意圖

（2）數學“四基”是相輔相成、和諧統一、螺旋遞進的關系．

由于數學知識的抽象性，在數學學習過程中，學生需要通過動手操作學具或畫圖等直觀手段，引發相應的數學思考，從而幫助理解所學的數學知識，并在數學知識的實踐與運用過程中獲得基本技能[11~15]．在基本技能獲得的過程中，學生不僅積累了操作活動經驗，而且積累了重要的思維活動經驗，尤其是積累了抽象的經驗、歸納的經驗和演繹的經驗等基本活動經驗，這些活動經驗都是后續數學學習的重要基礎．當數學活動經驗積累到一定程度，將在學生腦海里促進形成某種較為穩固的思維模式，這就形成了數學思想，當數學思想形成后，將進一步改良學生己有的認知結構，進一步完善己經形成的知識體系，同時，將從策略和方法上更好地促進新的數學知識的學習和新的技能的獲得，具體如圖2所示[16]．

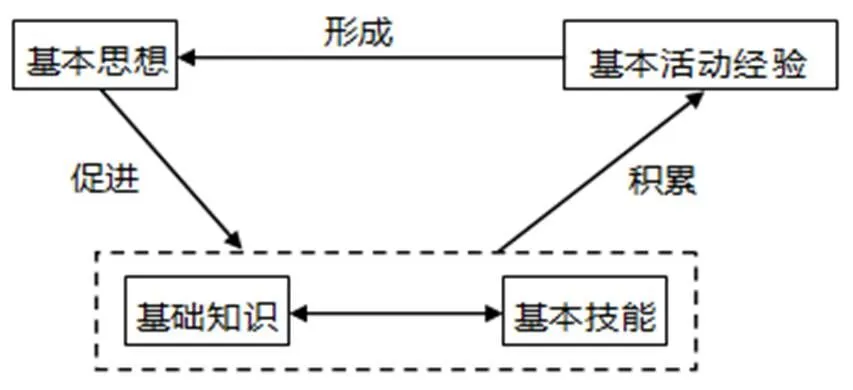
圖2 “四基”內部關系

（3）數學“四基”是知識系統和經驗系統的有機體．

基礎知識和基本技能形成了學生的知識系統，而基本活動經驗形成的是經驗系統，兩個系統有機結合、相互促進才構成完整的數學知識結構．這個結構形成的紐帶，就是數學活動．所以，數學活動的過程就是“經驗化”的過程．“雙基”只有通過經驗化，才能夠真正成為學生的數學素養．但是由于學生的原始經驗是模糊的、片面的、不嚴謹的，所以要使“基本活動經驗”更加確切、有效并且合理，就需要經歷一個形式化與概念化的過程．由于數學知識本來具有確定性和嚴謹性，所以經歷了形式化和概念化的“基本活動經驗”才能夠很好地融入“雙基”之中．兩個系統相互促進、相互結合才能讓學生獲得完整的數學知識．如圖3所示[27]．

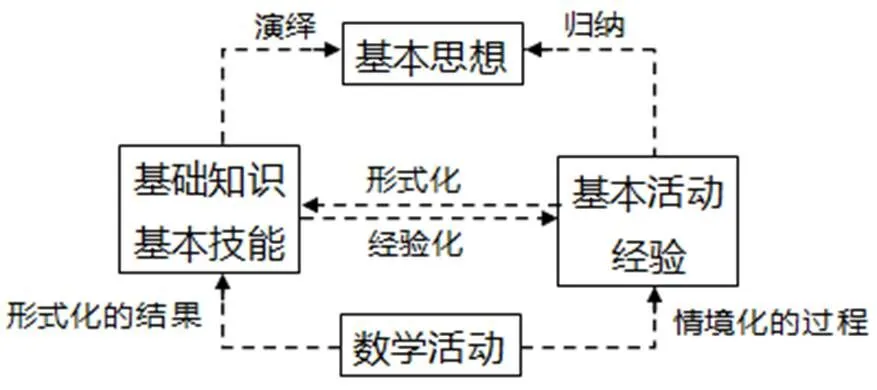
圖3 數學“四基”的關系結構

3.2 數學“四基”的外部關系

數學“四基”的外部關系主要指“四基”與數學課程“三維”目標之間的關系．

數學“四基”與數學課程“三維”目標聯系密切，數學“四基”內部的相輔相成、和諧統一和螺旋遞進的關系，促進了數學課程“三維”目標的整體實現．“四基”中的“基礎知識”和“基本技能”對應著“三維”目標中的“知識與技能”維度，“基本思想”和“基本活動經驗”對應著“三維”目標中的“過程與方法”維度．教師在“雙基”教學基礎上，通過融入“基本思想”、“基本活動經驗”的教學，將更好地促進學生對“基礎知識”、“基本技能”的理解、掌握和運用，更好感悟數學的基本思想，積累數學的基本活動經驗，體會數學的神奇與魅力，體會數學的價值，獲得成功的體驗，提高學習的興趣，增強學習的信心，從而促進“三維”目標中的“情感與態度”目標的達成．

因此，數學“四基”內部的和諧統一將更好促進外部“三維目標”的整體達成，它們之間的關系如圖4所示[16]．

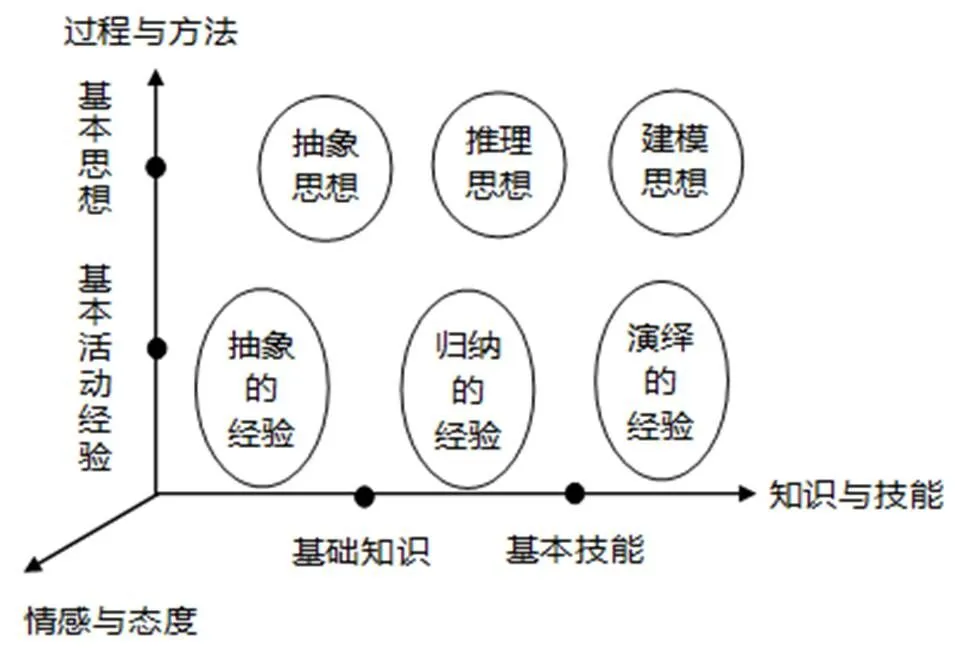
圖4 數學“四基”與“三維”目標關系

4 數學“四基”的教學實踐

數學“四基”要從理論走向實踐，才能更好體現其價值，查閱與數學“四基”相關并發表于核心期刊的22篇文獻，其中與數學“四基”教學相關的文獻有12篇，關注最多的主題是教學中怎樣有效滲透數學思想和數學活動經驗，并且多以課為例．

在教學中如何積累學生的數學活動經驗的觀點主要有以下幾種：

（1）參與建構，積累感性經驗——經歷擴展，積累估測經驗——自主探索，積累遷移經驗——解決問題，積累思辨經驗[28]；

（2）經歷探究，積累直接經驗——巧設情景，豐富間接經驗——內培外引，提升思維經驗——尊重起點，避免經驗越位[29]；

（3）順應多數學生的觀點，激活數學活動經驗——放大少數學生的思路，提升數學活動經驗[30]；

（4）鞏固舊知，激活“經驗”——操作實踐，拓展“經驗”——順應新知，建構“經驗”——返璞生活，提升“經驗”[31]；

對教學中如何滲透數學思想有以下幾點建議：

（1）教師要適時尋求數學思想滲透的可行性，重視數學思想的滲透與學生感悟的過程性，引導學生在反思中提煉數學思想[32]；

（2）在背景展示中揭示數學思想，在知識探索中滲透數學思想，在實踐操作中形成數學思想[33]；

（3）課堂教學中滲透數學思想的語言，不同于講解數學思想的語言．數學思想不是在講授知識時生拉硬扯、牽強附會地闡述的，而是融入其中，因勢利導、水到渠成地滲透的，也不是擺開架勢、長篇大論地傳授的，而是潛移默化、畫龍點睛地滲透的[34]；

（4）教學中應該從整體著眼，把數學基木思想真正看成教學的有機組成，有目的、有計劃地、連續地進行數學思想滲透活動[35]．

5 研究展望

綜上可知，目前對數學“四基”產生背景的研究較為全面，對基礎知識和基本技能的內涵界定也非常明確，對數學基本思想和基本活動經驗內涵的探討以及對數學“四基”內外部關系的探討雖然還沒有完全達成共識，但形成了一些共同觀點．另外，對數學“四基”教學的案例討論也較為豐富，突出了數學“四基”教學的理論與實踐的融合性[36~46]．

當然，也應該清醒認識到目前研究尚存在如下問題．

首先，缺乏數學“四基”教學系統全面的研究．現有文獻基本都是以某一課為例進行剖析并提出教學建議，缺少對數學“四基”教學的共性研究、頂層設計以及操作策略研究．

其次，缺失數學“四基”教學的評價研究．數學教學是否真正落實了四基，學生在教學中是否真正達成了數學“四基”目標，目前文獻尚少提及．

因此，有關數學“四基”的研究還需要進一步深化和拓展．

（1）“基本思想”和“基本活動經驗”的內涵研究仍然需要持續和深入，應該進一步明確數學“四基”，特別是基本思想和基本活動經驗的內涵與外延，對2011版課標有關“基本思想”和“基本活動經驗”的案例進行補充，幫助教師更好地理解和落實“四基”．

（2）深度挖掘“四基”的內部關系．“基本思想”和“基本活動經驗”是在“雙基”的基礎上新增的兩個“基本”，在教學中重點關注這兩個“基本”的思路是正確的，但是在關注“基本思想”和“基本活動經驗”的同時，不能忽視“基礎知識”和“基本技能”的發展與落實．需要進一步厘清“四基”的內部邏輯關系，把“四基”作為一個有機整體進行研究和落實．

（3）拓展“四基”的外部關系研究．比如，“四基”與核心素養的關系、“四基”與數學文化的關系，“四基”與數學素養的關系，“四基”與創新意識和能力的關系等，這些研究都將為良好的數學教育提供有力支撐．

（4）提升數學“四基”的教學實踐研究．圍繞體現數學“四基”的教學設計、教學實施和教學評價進行相關研究，突出數學“四基”教學的共性研究、頂層設計以及操作策略研究，在提升理性認識的基礎上更方便一線教師操作遷移；由于數學“四基”在教學實踐中的落實是其提出的根本訴求，因此要關注數學“四基”教學的評價研究，特別是“基本思想”和“基本活動經驗”屬于隱性目標，其在教學中的顯性評價的訴求更為迫切．

[1] 中華人民共和國教育部．全日制義務教育數學課程標準（2011年版）[M]．北京：北京師范大學出版，2011．

[2] 楊豫暉．數學雙基教學的發展、爭鳴與反思[J]．中國教育學刊，2010，（5）：34-37．

[3] 課程教材研究所．20世紀中國中小學課程標準·教學大綱匯編·數學卷[M]．北京：人民教育出版社，2001．

[4] 李潤泉，陳宏伯，蔡上鶴，等．中小學數學教材五十年：1950—2000[M]．北京：人民教育出版社，2008．

[5] 中華人民共和國教育部．全日制義務教育數學課程標準：實驗稿[M]．北京：北京師范大學出版，2001．

[6] 孫曉天．“四基”：十年數學課程改革最重要的收獲[J]．基礎教育課程，2011，（Z2）：34-37．

[7] 張奠宙，何文忠．交流與合作——數學教育高級研討班15年[M]．南寧：廣西教育出版社，2009．

[8] 宋乃慶，張奠宙．小學數學教育概論[M]．北京：高等教育出版社，2008．

[9] 中華人民共和國教育部．義務教育數學課程標準（2011年版）解讀[M]．北京：北京師范大學出版社，2012．

[10] 史寧中．數學思想概論（第一輯）：數量與數量關系的抽象[M]．長春：東北師范大學出版社，2008．

[11] 王光明，張楠，周九詩．高中生數學素養的操作定義[J]．課程·教材·教法，2016，（7）：50-55．

[12] 王光明，廖晶．“探索世界”范式及其對數學教育的啟示——ICME12獲獎報告述評[J]．課程·教材·教法，2013，（12）：116-119．

[13] 王光明，宋金錦，佘文娟，等．建立中學數學英才教育的數學課程系統——2014年中學英才教育數學課程研討會議綜述[J]．課程·教材·教法，2014，（5）：122-125．

[14] 王光明，佘文娟，宋金錦．基于NVivo10質性分析的高效數學學習心理結構模型[J]．心理與行為研究，2014，（1）：74-79．

[15] 王光明，張曉敏，王兆云．高中生高效率數學學習的智力特征研究[J]．教育科學研究，2016，（3）：48-55．

[16] 蘇明強．數學“四基”的內涵、關系與應用[A]．北京師范大學．首屆華人數學教育會議論文集[C]．北京師范大學，2014．

[17] 史寧中，柳海民．素質教育的根本目的與實施路徑[J]．教育研究，2007，（8）：10-14，57．

[18] 張奠宙，竺仕芬，林永偉．“基本數學經驗”的界定與分類[J]．數學通報，2008，（5）：4-7

[19] 單肖天，景敏．數學活動經驗及其對教學的影響[J]．課程·教材·教法，2008，（5）：41-44．

[20] 徐斌艷．面向基本數學活動經驗的教學設計[J]．中學數學月刊，2011，（2）：1-4．

[21] 朱黎生，沈南山，宋乃慶．數學課程標準“雙基”內涵延拓的教育思考[J]．課程·教材·教法，2012，（5）：41-45．

[22] 王新民．論數學活動經驗的基本內涵及其形成條件[J]．課程·教材·教法，2013，（11）：55-60．

[23] 張奠宙．數學“雙基”教學的理論與實踐[M]．南寧：廣西教育出版社，2008．

[24] 張丹．數學課程目標：從“雙基”到“四基”從“兩能”到“四能”[J]．中小學管理，2012，（4）：10-12．

[25] 崔英梅，孔凡哲．“四基”理論實踐探索中問題分析與改進對策[J]．中國教育學刊，2014，（3）：53-57．

[26] 張奠宙，鄭振初．“四基”數學模塊教學的構建——兼談數學思想方法的教學[J]．數學教育學報，2011，20（5）：16-19．

[27] 于佳．面向基本數學活動經驗的教學設計的若干問題研究[D]．陜西師范大學，2013．

[28] 蔡文美．經歷認知過程積累數學經驗——“面積單位”的教學探索[J]．教學與管理，2012，（29）：51-53．

[29] 孫春戀．例談學生基本數學經驗積累的課堂指導[J]．教學與管理，2012，（26）：41-43．

[30] 陳賽．讓學生的“數學活動經驗”生根發芽[J]．教學與管理，2012，（29）：45-46．

[31] 呂程，蔡慶有．思維經驗：數學活動經驗的內在精髓[J]．教學與管理，2013，（29）：37-39．

[32] 盧杰夫．教學有形思想無形——例談小學數學教學中數學思想的滲透[J]．山西教育（教學），2014，（12）：51-52．

[33] 康克．思想就在身邊——例談數學思想的教學演繹[J]．廣西教育，2015，（1）：61．

[34] 顧沛．小學數學教學也要注重滲透數學思想[J]．小學教學（數學版），2012，（Z1）：14-18．

[35] 胡曉敏．談小學計算教學中數學基本思想的理解與落實[J]．數學學習與研究，2014，（6）：60-61．

[36] 章勤瓊，徐文彬．試論義務教育數學教師專業素養及其結構——基于教師專業標準與數學課程標準的思考[J]．數學教育學報，2016，25（4）：69-73．

[37] 黃友初．教師課堂教學行為的四個要素[J]．數學教育學報，2016，25（1）：72-74．

[38] 吳立寶．初中數學教材代數內容的國際比較研究[J]．數學教育學報，2016，25（4）：33-36．

[39] 顧繼玲．聚焦“基本數學活動經驗”[J]．數學教育學報，2016，25（1）：34-37．

[40] 呂寶珠．中學數學教師對數學和科學課程整合態度的調查——以優質中學為例[J]．數學教育學報，2016，25（3）：61-65．

[41] 李大永，章紅．基于整體把握的運算主線下的“分數指數冪”教學[J]．數學教育學報，2016，25（1）：61-63．

[42] 方均斌，梁凱，朱玲．數學問題教學的五個探索點[J]．數學教育學報，2016，25（1）：47-50．

[43] 曹一鳴，王萬松．高中概率統計內容設置的國際比較——基于15個國家數學課程標準的研究[J]．數學教育學報，2016，25（1）：1-4．

[44] 葉志強，張輝蓉．數學文化與職前小學教師教育[J]．數學教育學報，2016，25（3）：56-60．

[45] 吳駿，汪曉勤．初中數學教師HPM教學的個案研究[J]．數學教育學報，2016，25（1）：67-71．

[46] 韓繼偉，黃毅英，林智中．初中數學教師的學科知識研究[J]．數學教育學報，2016，25（2）：49-54．

[責任編校：周學智]

Current Situation and Prospect of Mathematics “Four Basics”

ZENG Zheng1, YANG Yu-hui2, WU Jin-yan3

(1. Foshan University, Guangdong Foshan 528000, China;2. Hainan Normal University, Hainan Haikou 571158, China;3. The Third Primary School of QiongShan, Haikou City, Hainan Haikou 571100, China)

Mathematics “Four Basics” had been an important and hot point for Chinese mathematics education in current years, especially after the issue of “mathematics curricular standards for full compulsory education (2011)”, and related researches had become more abundant. 194 papers could be found in CNKI if we used mathematics “Four Basics” as key word. The mathematics “Four Basics” researches could be divided into four parts: the forming and development of mathematics “Four Basics”, the connotation of mathematics “Four Basics”, the relationship of mathematics “Four Basics”, and the teaching of mathematics “Four Basics”. The combing and analysis on those research results could be viewed as a reference for its further research.

mathematics “Four Basics”; combing; relation; teaching practice

G40-034

A

1004–9894（2017）02–0066–05

2017–02–21

天津市哲學社會科學規劃（重點）項目——立德樹人背景下中學生學科核心素養測評——以語數外為例（TJJX16-007）

曾崢（1961—），男，廣東蕉嶺人，教授，碩士研究生導師，主要從事不等式、數學教育研究．楊豫暉為本文通訊作者．