基于SVR的股票價格預測研究
張柯柯
【摘 要】本文采用支持向量回歸(SVR)對股票價格進行預測分析,以中國人壽(601628)為對象進行建模和預測研究。選取中國人壽2015-2016Q1的股票技術指標等數據作為訓練樣本對下一交易日的開盤價進行預測,以2016年4月的數據進行檢驗,并通過圖像擬合來驗證SVR用于股票預測的可行性和準確性。
【關鍵詞】股票預測;支持向量機
1.引言
隨著我國證券市場的深化發展,市場參與人數的增加,如何預測股票價格走勢受到了廣大投資者的關注。而股票市場的價格波動,一方面受IPO與資金的供求關系、大小非解禁和減持效應的影響;同時受宏觀經濟周期、貨幣供給、物價變化、利率水平等宏觀經濟因素和公司經營管理、治理結構等微觀結構的影響;另一方面股票市場上投資者行為和政策性因素也會對股票市場波動產生重要影響。
為了保證投資收益降低風險,股票價格預測成為投資者關注的熱點,同時股票市場的波動與貨幣政策、財政政策的變化密不可分,股票市場作為資本市場的重要組成部分,對推動經濟的發展發揮重要作用,因而政策制定者也迫切需要了解宏觀調控對股票市場的影響,預測股票價格波動。國內外學者們從不同角度,采用各種方法對股票價格做仿真實踐與理論研究,如時間序列模型模型與神經網絡模型。在時間序列預測模型方面,史書真(2013)[1]介紹了ARMA模型在股票預測中的應用,對中國石油等股票進行仿真,得出ARMA模型能較好的預測股價;徐楓(2006)[2]則用GARCH模型對我國航空業代表性股票進行仿真。在神經網絡應用于股票預測方面:張健(1997)[3]研究了BP神經網絡在股票價格預測中的應用,對“陸家嘴”等股票的樣本數據進行學習和檢驗,得出BP神經網絡在股票分析與預測中有一定的應用前景。陳政等人(2010)[4]利用RBF社交網絡對生政綜合指數進行仿真,得到了較好的預測效果。然而這些模型有其局限性,如存在局部極小值、欠學習、過學習等問題,SVM模型則較好的解決了上述問題,被廣泛的應用于證券領域,并取得了很好的效果。
2.SVR
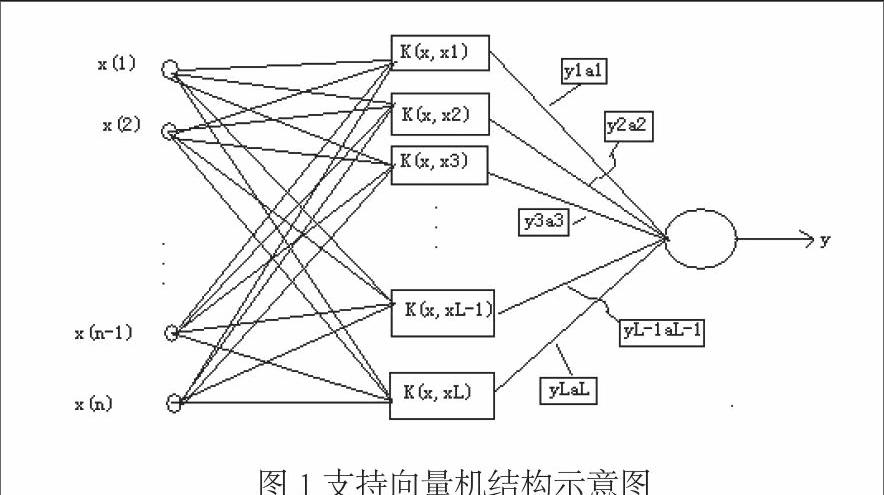
支持向量機(support vector machine, SVM)是美國Vapnik教授于1990年代提出的一種機器學習方法。SVM的基本思想是將原始非線性訓練數據集通過非線性途徑映射到一個高維特征空間,使其變得線性可分,然后在該特征空間中找到一個具有最大分離距離的超平面[5]。支持向量機的結構示意圖可以表示如下:
支持向量機的網絡結構類似于神經網絡,其中輸入層是為了存貯輸入數據;中間層是通過對樣本集的學習和選擇;其輸出則是若干中間層節點的線性組合。
支持向量回歸(SVR)是支持向量在函數回歸領域的應用。對于非線性SVR,其基本思想是通過將輸入向量映射到高維特征空間中,然后在此高維空間中再進行線性回歸,從而取得在原空間非線性回歸的效果。使用支持向量回歸(SVR)解決回歸問題,首先應選擇合適的核函數.常見的核函數包括線性核函數、多項式形式核函數、RBF(徑向基)核函數、Sigmoid核函數等。本文選擇式(1)所示的RBF(徑向基函數)作為核函數.其次要選取合適的 RBF核參數、懲罰因子C和損失函數。 (1)
3.實驗仿真
3.1 模型指標體系的構建
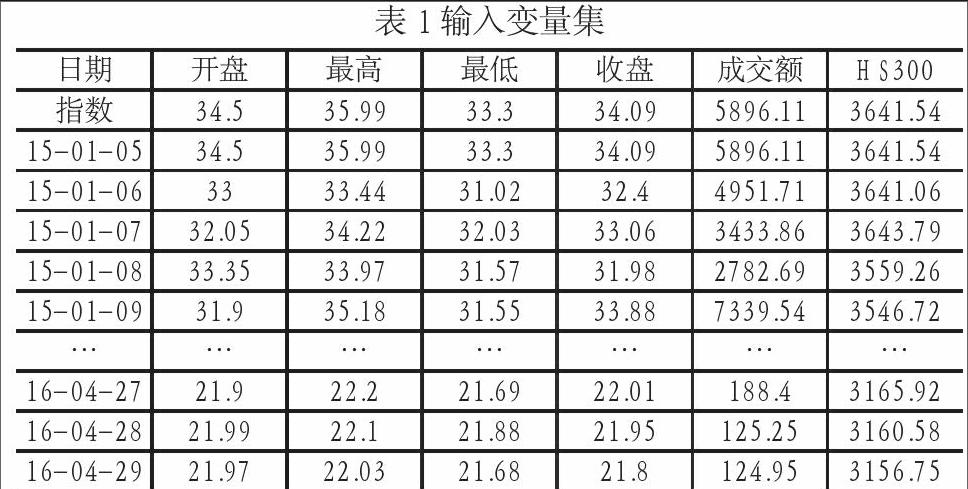
本文以上海證券交易所上市的中國人壽(601628)的股票數據進行預測,數據來源于WIND金融數據庫。選取中國人壽(601628)2015年1月5日至2016年4月29日期間323個交易日的數據作為樣本集,其中2016年4月份(后19個交易日)的數據作為預測樣本,其余數據作為訓練樣本。以開盤價(元),最高價(元,最低價(元),收盤價(元),成交額(百萬),滬深300指數作為股票價格預測的輸入變量集,數據見表1所示;以下一日開盤價作為輸出變量。
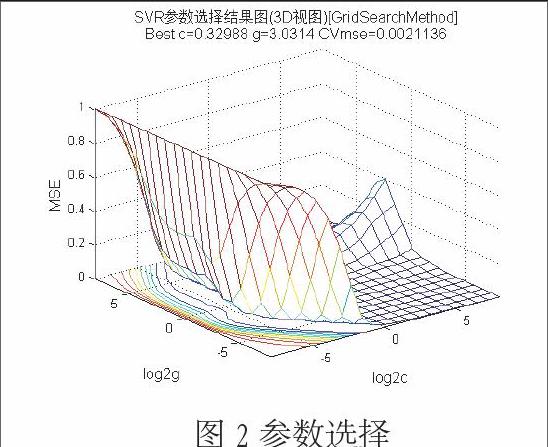
3.2 SVR參數選擇
SVM的性能很大程度上依賴于核函數的選擇,但沒有很好的方法指導針對具體問題的核函數選擇。SVMcgForRegress函數的目標是為SVM算法尋求一對最佳的參數c和g。
3.3實驗結果分析
本文用SVR對中國人壽(601628)股票價格的預測結果如圖3所示,從圖中可見預測值與實際值的整體趨勢基本符合實際數值的趨勢。
從仿真的結果來看,可以看出SVR是可以對股票價格進行預測的,為投資者提供更好的投資依據,但在SVR核函數的選擇及參數選定方面需進一步 研究。
參考文獻:
[1]史書真.股價時間序列的分析與預測研究[D].大連:大連理工大學,2013.
[2]徐楓. 股票價格預測的GARCH模型[J].統計與決策, 2006(18):107-109.
[3]張健,陳勇,夏罡,何永保.人工神經網絡之股票預測[J].計算機工程, 1997(2):52-55.
[4]陳政,楊天奇. 基于RBF神經網絡的股票市場預測[J]. 計算機應用與軟件, 2010, 27(06):108-110.
[5]鐘用祿,李海山,劉發圣,譚鵬,張尚志,張成.基于PCA-SVR的燃煤鍋爐NO_x排放預測[J]. 熱力發電,2015(1):87-90.
[6]Vladimir Vapnik. The Nature of Statistical Learning Theory(Second Edition)[M]. Springer Verlag, 2000.

