趣味生動化的全概率公式教學設計研究

周游

（湖南財政經濟學院 數學與統計學院，湖南 長沙 410205）

趣味生動化的全概率公式教學設計研究

周游

（湖南財政經濟學院 數學與統計學院，湖南 長沙 410205）

本文對全概率公式的新型教學模式進行研究，讓授課更為趣味化、生動化.通過設置游戲、播放影片、設計調查問卷等新穎方式引入、闡述以及探究問題.選取學生感興趣的實際問題，啟發引導學生參與解決，使學生深化對全概率公式理解，掌握全概率公式應用技巧.

全概率公式；趣味生動；應用技巧

全概率公式是概率論與數理統計課程中一個非常重要的內容，在教學中要做到“法理相融”，即全概率的“算法”和“算理”的滲透理解.按照傳統的教學模式，學生對該公式難以深入理解和掌握[1].因此，本次教學通過一個游戲的設置以及相關影片的放映，極大地激起學生的興趣，與學生高度互動，讓學生在玩樂中理解全概率公式的思想.典型問題教學啟發、步步推導、與學生產生共鳴，增強學生的感知認識；選取學生感興趣的彩票購買中獎、敏感性問題調查方式等問題，積極實施提問誘導，引導學生參與解決實際問題中，進一步深化對全概率公式理解，掌握全概率公式應用技巧[2-3].

1 問題引入：游戲和電影

1.1 情境創設，游戲引入

教師準備三個不透明的箱子和一張百元鈔票.把錢放入某一個箱子中（只有教師知道錢在哪），現在請大家猜測.假如有同學猜測是1號箱，先不著急打開它，而從剩下的兩個箱子當中，挑選一個沒有錢的箱子，比如說2號箱，打開.這時候，給同學一個改選的機會，是堅持1號箱還是改選成3號箱？

思考：當教師首次打開一個沒有錢的箱子時，同學是否應該改變初次選擇？

1.2 師生互動，進行游戲

選擇幾位同學來進行游戲.并鼓勵大家在課后進行這樣的游戲，經過多次實驗，把實驗結果記錄下來——總的試驗次數是多少，堅持選擇贏錢的次數和改變選擇贏錢的次數分別是多少，嘗試找到統計規律性.

1.3 播放影片，啟發誘導

這看似是一個簡單的游戲，實際上是一個嚴格的概率統計問題.這個問題興起于上個世紀90年代，曾經在美國引起了非常廣泛的興趣和討論，甚至還引起了美國中央情報局的關注，他們認為這個問題的分析解答可以應用到情報分析當中.播放《決勝21點》里面關于三門問題的一個片段.說明之前做的游戲實質上就是一個三門問題，即三個箱子表示三扇門，有錢代表門后有車，否則表示門后是羊[4].

電影給出了正確答案，但是大部分學生還沒有完全理解，接下來教師給出數學推導.

1.4 問題求解，闡述思想

這個問題要解決的是是否改變初次選擇，而是否改選取決于哪種情況下選中汽車的概率更大.

把改選“選中汽車”看作目標事件A，把初次選擇的結果分別記為B1和B2，A受B1和B2的影響，即A=AB1∪AB2，由于這兩個事件不可能同時發生，也就是說兩者互不相容，根據互不相容事件并集的概率等于概率之和，A的概率就是這兩部分的和.

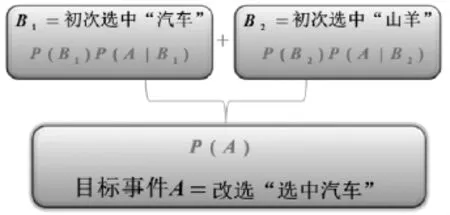
A=AB1∪AB2

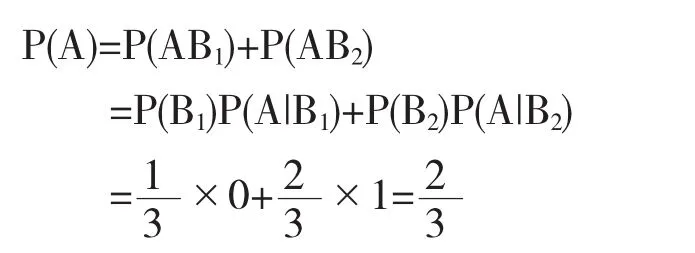
結論：當初次打開一扇有山羊的門時，是否應該改變初次選擇？盡管不能保證一定能獲得汽車，但是至少可以將獲得汽車的概率從提高到.

內容小結：實際上，如果遇到一個復雜事件，直接去求概率可能比較困難，不妨將這個復雜事件分解為若干個簡單事件來進行求解.這個問題的求解過程就是將一個復雜事件A分解為較為簡單的兩個事件AB1和AB2，然后將概率的加法公式和乘法公式結合起來，從而求得A事件的概率.全概率公式就是基于這樣一種分解的思想.

2 全概率公式

2.1 闡述分解過程（PPT動畫展示分解圖示）

一般地，對于一個復雜事件A，要對其進行分解，首先要把整個樣本空間分解為n個事件B1,B2, LBn，要求這n個事件之間是互斥的，并集是整個樣本空間，也就是說B1,B2,LBn是樣本空間S的一個完備事件組（劃分）.由于樣本空間的分解，事件A也被分解成了n個互斥的事件ABi(i=1,2,L,n)，因此，A可以表示這n個事件的并

2.2 推導公式（黑板演示推導過程）

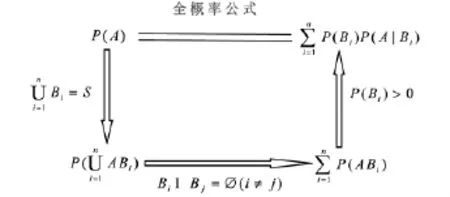
2.3 全概率公式

定理 設事件組B1,B2,L,Bn是一個完備事件組，P(Bi)＞0，i=1,2,L,n,則對于任一事件A，

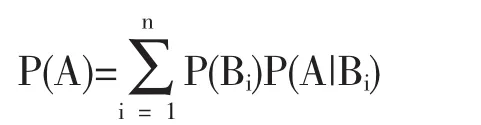
稱為全概率公式[5].

說明：若把事件A看作結果，B1,B2,L,Bn就是導致該結果發生的原因，故全概率公式也稱由因導果公式.其實質是結果在各原因下的條件概率的加權平均.

注意：全概率公式的思想是復雜問題的分解；關鍵是找到合適的劃分.

3 解題步驟

3.1 實例引出

通過具體的實例來引導學生概括應用全概率公式解題的步驟.

引例 一位同學趕來上課，他可能乘坐地鐵、公交或是出租車，乘坐這三種交通工具的概率分別為50%，30%和20%.已知乘坐這三種交通工具遲到的概率分別為0.05,0.2,0.1，求該同學遲到的概率.

分析：顯然，乘坐這三種交通工具都有可能導致上課遲到，我們可以將遲到這一事件看作結果，記為事件A，它產生的原因有這三個，分別記為B1, B2,B3，而且，題目已知B1,B2,B3發生的概率，以及在B1,B2,B3發生的條件下A事件發生的概率，這是一個典型的已知原因求結果的問題，用全概率公式.

3.2 總結步驟

一、找到合適的完備事件組Bi(i=1,2,…,n)；二、求P(Bi)；三、求P(A|Bi)；四、利用全概率公式求目標事件A發生的概率.

4 例題精講

4.1 彩票問題

生活中，同學們對彩票并不陌生.大家是否思考過這樣一個問題：購買彩票的先后次序不同是否影響購買者的中獎概率？針對這個問題，引入下面簡化的摸獎模型：

例1（摸獎模型） 設在10張彩票中有兩張獎券，求第一個人和第二個人摸到獎券的概率分別是多少？

擴展：第三個人中獎的概率是多少？（復合實驗）

注意：在這個問題的解答當中可以看出，除了典型的已知原因求結果的問題，在這樣的復合試驗中也可以利用全概率公式，我們可以將最后一次的實驗結果看作目標事件，前幾次試驗結果的交叉為樣本空間的一個劃分，根據全概率公式的思想，利用加法公式和乘法公式進行推導,得到全概率公式的拓展形式.

說明：中獎概率與購買次序無關.同樣地，對于抽簽問題，這個結論也是成立的.因此，無論是摸獎還是抽簽，由于每個人獲獎的機會都是相同的，大家無需爭先恐后，安靜地排好隊依次抽取就好.

4.2 射擊問題

學生練習：甲、乙、丙三人同時獨立地對飛機進行射擊，飛機被一人、兩人、三人擊中的概率分別為0.36,0.4和0.14，根據經驗，飛機被一人擊中而被擊落的概率為0.2，被兩人擊中而被擊落的概率為0.6，若三人都擊中，飛機必定被擊落.求飛機被擊落的概率.

分析：飛機被擊落是結果，原因分別是有一人、兩人、三人擊中飛機，直接用全概率公式計算.

將原題改為：

例2 甲、乙、丙三人同時獨立地對飛機進行射擊，三人中的概率分別為0.4，0.5，0.7.飛機被一人擊中而被擊落的概率為0.2，被兩人擊中而被擊落的概率為0.6，若三人都擊中，飛機必定被擊落.求飛機被擊落的概率[6].

分析：在該問題中，顯然飛機被擊落是結果，原因是有一人、兩人、三人擊中飛機，但是這三個原因的概率未知，還要先求解出來.

內容小結:在解決這一類問題的時候，一定要區分原因和結果.這里的原因就是樣本空間的劃分.

5 思考探究

要調查期末考試當中學生的作弊情況，直接利用是否作弊這種簡單的調查問卷調查，其結果差強人意.對于敏感性問題，涉及到個人隱私，大家都不愿意說真話.現在請同學幫忙設計一種調查的方式，盡可能地保護大家的隱私.

教師提供一種方案：被測試者進入一個無人的房間，房中有一個箱子，箱子里有裝有若干紅球和白球，他從這個箱子隨機抽出一個球，看過顏色后放回.如果取得白球，就回答：你的生日是在7月1日前嗎？如果取得紅球，就回答：你在期末考試中作弊了嗎？將結果勾在一張只有“是”和“否”的答卷上.

請同學思考：為什么用這種方式大家愿意說真話？又怎樣通過調查結果得到期末考試作弊率？

6 總結

這節課講授了全概率公式這一重要公式.全概率公式是由加法公式和乘法公式結合起來的，公式應用的思想是復雜事件的分解，分解的關鍵是找到合適的劃分.全概率公式也叫做由因導果公式，如果要由結果來探究產生的原因，那就要用到下一節內容——貝葉斯公式.

7 結束語

本次教學設計本著“讓生活走進數學課堂、讓數學回歸生活”的理念，落實“以教師為主導，以學生為主體”的理念，在教學中盡可能突破傳統模式，讓授課更為趣味化、生動化.讓學生在發現問題、分析問題、解決問題的過程中，建立了“用數學”的意識，培養了“用數學”的能力，體驗了“用數學”的樂趣，教學效果良好.

〔1〕趙云平.關于全概率公式的教學探析[J].農村經濟與科技,2016,27(22):239-241.

〔2〕馮衛東.情境教學操作全手冊[M].南京：江蘇教育出版社,2010.

〔3〕秦玉芳,丁艷鳳,鄭小琪.淺談情境教學法在概率統計中的應用[J].高教學刊,2016（15）:113-114.

〔4〕張慧.關于“概率論與數理統計”課程中案例教學的研究[J].求知導刊,2015,24:136.

〔5〕劉宏超.概率論與數理統計[M].北京：清華大學出版社,2011.

〔6〕吉家鋒.在課堂上巧妙嵌入有趣教學實例,提高學生學習全概率公式的興趣和質量[J].高等教育研究,2014,31(3):32-34.

G642.4

A

1673-260X（2017）04-0219-03

2017-02-03

湖南省教育廳科學研究項目(14C0192);湖南財政經濟學院教學改革項目(2016xjjg006)