如何解決小學數學中的疑難問題

文/李天均

如何解決小學數學中的疑難問題

文/李天均

當孩子向我們請教學習中的問題時，問題本身對家長或老師而言并不難，但是當我們給孩子講解如何解決問題時發現孩子們卻聽不懂。其原因是家長在用孩子們未來的知識在解釋現在的問題，而作為老師卻明知不能這樣做，可不知應該如何應用學生現有的知識去分析解決問題。如：小學五年級上學期學習小數除法時，有這樣一道數學動腦筋的題。

一輛汽車共載客50人。一部分買A種票，每張0.8元；另一部分買B種票，每張0.3元。A種票比B種票多收入18元，買A種票的有多少人？

這道題如果用列方程解決問題的方法并不難做，設買A種票的有x人，那么買B種票的有（50-x）人。列方程為：0.8x-0.3×（50-x）=18，解方程得x=30；如果設買B種票有y人，則買A種票的有（50-y）人，列議程為（50-y）×0.8-0.3y=18，解方程得y=20，買A種票的50-y=50-20=30（人），由于學生沒有學過列方程解決問題的方法，我們可從方程里推導出求買A種票人數的算術方法。

由0.8x-0.3x（50-x）=18 可推出：（0.3×50+18）÷（0.8+0.3）又從第二種方法中推導出：50-（50×0.8-18）÷（0.8+0.3）來求出買A種票的人數。

可是現在問題又出現了（50×0.3+18）和（50×0.8-18）求得什么？（0.8+0.3）是否是一張A種票與一張B種票的總價？（0.8+0.3）與（50×0.3+18）和（50×0.8-18）是一種什么樣的關系，家長和許多老師都沒有辦法說清楚，而學生又沒有學過列方程解決問題的方法，有些小學數學教師想到了用解決“雞兔同籠”中的假設法來解釋又好象說不清。

說到“雞兔同籠”，學生是在四年級下學期學習的，教材中先用了“列表法”解決問題，再推導出“假設法”來解決問題，而列表法中有一種有趣的現象；先假定全部是一種動物，然后在逐一不斷地互換到全部是另一種動物為止，它們的腳的總數也隨著不斷在增加或（減少）相同的數量。在這樣的過程中就會出現題中所需的答案，而以上的兩種方法與這種有趣的現象正好是用算術方法解決上面車票問題的最佳方法。

現在我們先回顧一下四年級里是如何解決“雞兔同籠”的問題的。

“籠子里有若干只雞和兔。從上面數有8個頭，從下面數有26只腳。雞和兔各有幾只？

方法一，列表法，先填寫下來，填完后找出正確答案。

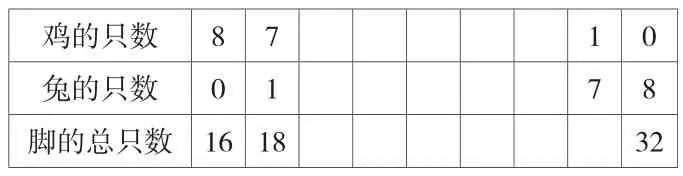
雞的只數8 7 1 0兔的只數0 1 7 8腳的總只數16 18 32

觀察這張表很快可得出雞有3只，兔有5只時，它們的腳的總數正好是26只。

方法二：假設法

再次觀察列表法中的表，從左往右看，先假設全部是雞，再把雞逐一換成兔，每換一次腳的總數就增加2，（兩種動物的腳的差），8只雞有16只腳，而現在腳有26只，相差（26-16）只，所以雞換成兔的只數應該是（26-2×8）÷（4-2）=5只，雞有8-5=3只。

而從右往左面容，則先假設全部是兔，求出雞的只數（即兔換成雞的只數）為：（4×8-26）÷（4-2）=3只，兔有8-3=5只。

由上可看出，應用列表法解決學生思維難度較大的題時不僅是較直觀，簡單的一種方法，同時又能誘導出其他方法的好方法。是非常值得我們老師提倡，家長使用的好方法。那么有人會提出數據較小時是很方便，但數據較大時不是會很麻煩嗎？確實存在這個問題，不過結合學生熟悉的估算思想就解決了。在列表前先估計一下腳的總只數與“全部設為雞”和“全部設為兔”時，哪個更接近或是在兩種之間，如果有較接近的就從接近的一邊列表解決，如果在兩種之間我們可以兩種動物數量相等開始列表來解決。

現在我們就用以上觀點，方法來解決兩種車票的問題。

方法：用列表法。

1張A種票（0.8元）比1張B種票（0.3元）貴所以兩種車票張數相同時A種票的總收入一定比B種票多。因此我們先假定各買25張票來列表：

A種票的總收入比B種票多（元）25 25 12.5 A種票的張數B種票的張數

從表中可以看出，各買25張時，A種票比B種票多收入12.5元，但比多收入18元還有一定的差距，不過從中我們不難看出買A種票的人一定比25人多，所以需要把買B種票的25人中要轉換一部分為買A種票。

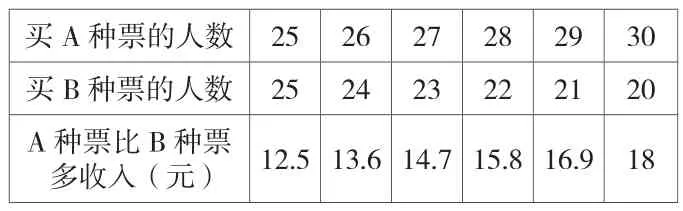
買A種票的人數25 26 27 28 29 30買B種票的人數25 24 23 22 21 20 A種票比B種票多收入（元）12.5 13.6 14.7 15.8 16.9 18

通過上面的列表法學生很好理解“買A種票30張比B種票20張多收入18元”。

再通過假設，列表、分析的方法我們又可以得出學生基本能理解的三種方法。

方法二，先假設兩種車票張數相等，再列表分析解答。

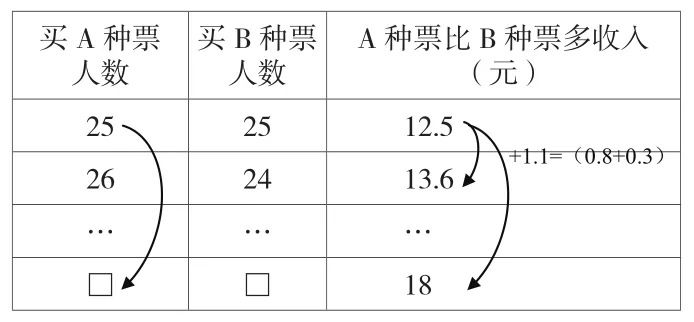
買A種票人數A種票比B種票多收入（元）252512.5 262413.6………□□18買B種票人數+1.1=（0.8+0.3）

分析，解答，①各賣25張時A種票比B種票多收入：25×0.8-25×0.3=12.5（元），②比多收入18元還少：18-12.5=5.5（元）。③把買B種票的1人轉換成買A種票時，A種票的總收入比B種票又多出1.1元（0.8+0.3）。④買B種票的人中轉換幾人買A種票才能多收入5.5元？5.5÷1.1=5（人）。⑤買A種票的共有多少人？25+5=30（人）。

答：買A種票的有30人。

方法三：先假設50人都買A種票，再列表分析并解答。

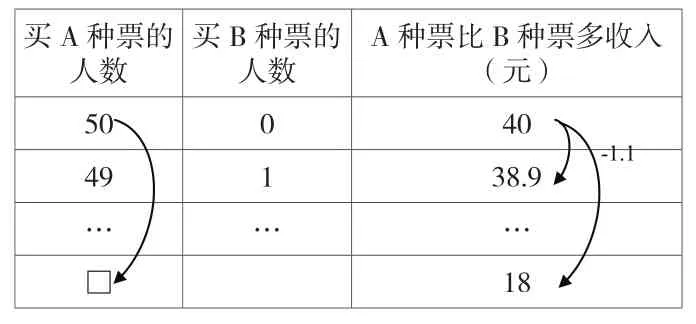
買A種票的人數A種票比B種票多收入（元）50040 49138.9………□18買B種票的人數-1.1

設全部買A種票，則A種票比B種票多收入40元，而中信息告訴我們只能多收入18元，那么我們需要把多收40元中轉化掉40-18=22元，由買A種票的1張轉化成買B種票時總收入只減少了0.8+0.3=1.1元，那么22元中有幾個1.1元，就需要把買A種票的幾個人轉換成買B種票，即22÷1.1=20（人）買B種票，所以買A種票的有50-20=30（人），列成綜合算式為：50-（50×0.8-18）÷（0.8+0.3）=30（人）。

方法四：先假設50人都買B種票，再列表，分析并解答。

買A種票的人數買B種票的人數0 50 A種票比B種票少收入15元1 49 A種票比B種票少收入13.9元1.1……□A種票比B種票多收入18元

由A種票比B種票少收入15元轉化到A種票比B種票反而多收入18元。就在總收入中需要一共轉化掉15+18=33（元），而每次由買B種票的人轉換成買A種票時，A種票比B種票多收入1.1元，所以由50人買B種票里要轉換33÷1.1=30人買A種票才能達到“A種票比B種票多收入18元”的要求。列成綜合算式為：（0.3×50+18）÷（0.8+0.1）=30（人）。

當我用以上方法給學生講解完時，有一個學生拿著作業來問我：“李老師，1張A種票比1張B種票貴0.5元（0.8-0.3=0.5），而題中不是說A種票比B種票多收入18元，我用18÷0.5求出買A種票36人，50-36求出買B種票14人怎么就錯了呢？”我說：“你先用36張A種票和14張B種票及單價檢驗一下總收入相差多少？”結果這個學生很快算出來了，0.8×36-0.3×14=28.5-4.2=24.6（元），這時我又問她：“你從這個結果想到了什么？”她說：“24.6元﹥18元，看來買A種票的36人多了，而買B種票的14人少了。”我接著說：“你能不能從36人買A種票，14人買B種票中用逐一轉換的方法得到正確結果呢？試試！”結果她經過6人次的轉換后得到了當30人買A種票，20人買B種票時A種票比B種票多收入18元。這個學生從她開始錯誤的理解中，經過檢驗、思考又找到了解決問題的另一途徑。

以上是我對這一問題的理解和給學生講解的思路和過程，如果對較用心的家長和老師能有所借鑒與啟迪我就很欣慰了，如若發現哪些地方有問題和不足請批評指正。同時，我正在思考這樣一問題，如果學生學會了列方程解決問題的方法后，再次讓學生做一做這道題，并與自述方法的分析解答過程比一比，不知學生的心里會感悟到些什么？

（作者單位：云南省麗江市實驗學校）