數學思想方法在有理數中的體現與應用

羅正剛

中圖分類號：G632 文獻標識碼：C 文章編號：1672-1578（2017）05-0107-01

數學思想方法是人們對數學科學研究的本質及規律的深刻認識，它是指導學習數學，解決數學問題的思維方式、觀點、策略和指導原則。它具有導向性、統攝性、遷移性的特點，它直接支配著數學的實踐活動。有理數是整個代數的基礎，有理數的運算是中學數學的基本運算，它所蘊涵的豐富內容深刻地反映了中學階段許多重要基本數學思想方法。

下面，本文就結合《全日制數學課程標準》中“有理數”的有關內容談談數學思想方法在教學的運用。

1 數形結合思想

“數形結合”是把比較抽象的代數問題與適當的圖形結合起來借助形象思維去認識、處理問題的一種思想方法。

“數無形、少直觀，形無數，難入微”，利用數形結合，可以將問題化難為易，化繁為簡，便于學生直觀理解，并提高形象思維能力。

數軸上的點表示有理數就是最簡的數形結合思想的運用，它對于學生理解有理數的相反數概念、經驗值概念，有理數大小的比較，以及有理數的加法，有理數的乘法等都有重要的幫助。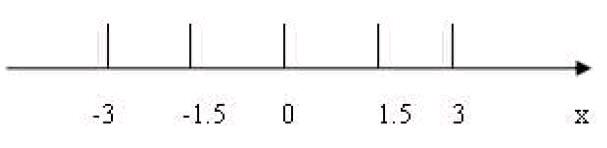

例如：“只有符號不同的兩個數叫做互為相反數”。若學生從形式上強行記憶概念，很難真正理解何為相反數。現在運用數軸（如圖），在數軸上畫出-3與3、-1.5與1.5所有對應的點，然后引導學生觀察這些點所在的位置特征，可以看到，表示為相反數的兩個點，分別位于原點的兩旁，且它們離原點的距離相等，這樣學生就有了形象的認識，且它們離原點的距離相等，這樣學生就有了形象的認識，不難理解了。這種由數想形、以形助數的方法不僅能提高學生的數形轉換能力，還能提高學生的遷移思維能力。

2 化歸思想

所謂“化歸”就是將所要解決的復雜問題轉化歸結為另一個較易解決的簡單問題或已經解決的問題。具體地說，就是把“新知識”轉化為“舊知識”，把“復雜”轉化為“簡單”，這樣學生學習時就容易理解和掌握了。

有理樓的知識上有許多地方都蘊藏著“化歸”的思想。而在有理數運算中體現的最為突出。有理數的運算都是先確定符號，再計算絕對值，在符號確定以后，絕對值的計算實際上就是小學所學過的數的運算問題。

例如：計算：① -10+（-3）， ② -10-（-7）， ③ （-3）÷1/2

解：① -10+（-3）

=-（10+3）（有理數加法轉化小學所學的加法）

② -10-（-7）

=-10+7（有理數減法轉化為有理數加法）

=-（10-7）（有理數加法轉化為小學所學的運算）

③ （-3）÷1/2

=（-3）×2（有理數除法轉化為有理數乘法）

=-（3×2）（有理數乘法轉化小學所學乘法）

可見，數學中利用化歸思想方法，可以另辟蹊徑，解決新問題，獲得新知識。教師若能在此章教學中，不失時機地對學生加以啟迪強化其化歸思維意識，那么在今后學習代數式的運算、解方程、函數變形等知識時，運用化歸思想會更加意識化。

3 分類思想

分類思想是一種邏輯劃分，它把數學對象劃分為不同的情形，分別進行研究，它是數學發現的重要手段。由于很多數學問題存在一些“不確定因素”，很難用“統一的標準”去解決，因此，必須把數學問題劃分成“塊”，然后針對不同的“塊”采取相應的解決辦法。可以說，分類討論的策略是“化整為零”，各個擊破。

在文章中對相反數、絕對值的概念都是運用了。分類討論的思想方法研究的。

例如，有理數的絕對值概念是從正數、負數、零三個方面討論。

（1）一個正數的絕對值是它本身。

（2）一個負數的絕對值是它的相反數。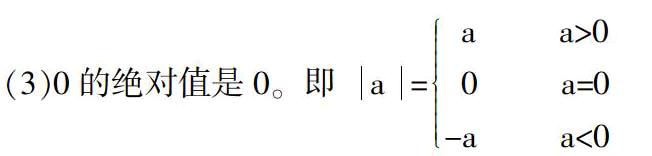

（3）0的絕對值是0。即 a= a a>0 0 a=0-a a<0

分類討論思想不僅運用在本章的概念中，而且還多次運用在有理數的運算中。

例如，有理數的加法法則就是通過四種情形的討論而概括出來的。

①同號兩數相加，結果取相同的符號，并把絕對值相加（這里的同號又分為兩加數同為正數或同為負數的情形）。

②絕對值不等的異號兩數相加，結果取絕對值較大的加數的符號，并用較大的絕對值減去較小的絕對值。

③絕對值相等的異號兩數相加（即互為相反數的兩數相加）結果為0。

④任何一個有理數與0相加結果仍得這個數。

另外，有理數的乘法、除法及乘方法則都是運用分類討論思想概括的。

由以上可以看到，數學思想方法在有理數中有了一些體現，這就要求我們以此為效載體加強數學思想方法教學。在教學中筆者體會到：在數學教學中有目的滲透教學思想方法并讓學生逐步領悟、掌握和學會運用數學思想方法，學生便可本質地學數學、做數學、用數學。