對筆算除法教學(xué)難點(diǎn)的思考
孫濱
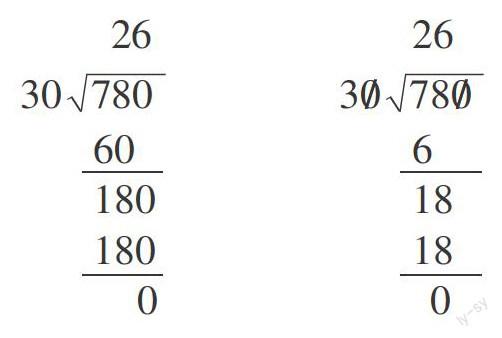
筆算除法在小學(xué)階段是一個(gè)重要的學(xué)習(xí)板塊。筆者在教學(xué)過程中發(fā)現(xiàn),當(dāng)過了一個(gè)學(xué)期或者一段時(shí)間后,大部分學(xué)生對筆算除法便又停留在模糊記憶的層次。這讓筆者不禁產(chǎn)生了疑問,為什么學(xué)生這么容易忘記筆算除法?筆算除法到底難在哪里?學(xué)生的思維斷點(diǎn)到底在哪里?
一、筆算除法難在哪里?
1.書寫格式
除法豎式為什么要寫成這樣的分層形式?為何不寫成跟加減乘一樣三行的形式?事實(shí)上,除法豎式的分層書寫是表示除法的過程和結(jié)果的需要,它的優(yōu)勢是既能表示出商與除數(shù)的積,又讓余數(shù)有了位置。這兩個(gè)數(shù)即是運(yùn)算過程的表達(dá),也是理解算理的過程,更是理解有余數(shù)除法的關(guān)鍵點(diǎn)。特別是運(yùn)算多位數(shù)除法時(shí),這種優(yōu)勢更是顯而易見。
2.負(fù)遷移
除法豎式是個(gè)全新的知識,容易受加減豎式的負(fù)遷移。從學(xué)生的學(xué)習(xí)來看,學(xué)生先學(xué)表內(nèi)除法豎式,容易將“商×除數(shù)”這一步虛化成抄寫被除數(shù)。即使教師在教學(xué)過程中刻意強(qiáng)調(diào)了筆算除法的運(yùn)算法則,學(xué)生依然是一頭霧水,只好“照搬硬套”。有人認(rèn)為,用“有余數(shù)除法”引入,可以避免這個(gè)非本質(zhì)的定勢和干擾。然而,筆者認(rèn)為這不符合知識的內(nèi)在邏輯順序。
3.方法多變
除法豎式相對其他三種運(yùn)算來說,變化多端。有時(shí)商在最高位上,有時(shí)首位不夠除,要看前兩位;有些“0”要移下來參加計(jì)算,有些可以省略計(jì)算;有些余數(shù)要添0,有些商要添0;試商又是除法運(yùn)算特有的難點(diǎn),等等。方法的多變,使學(xué)生理解、掌握也變得更難。
二、筆算除法教學(xué)策略的探討
1.科學(xué)呈現(xiàn)算理與算法
觀摩了俞正強(qiáng)老師的《筆算除法》(三年級)對我有了啟發(fā)。首先,通過加法、減法、乘法豎式與除法豎式的對比,引發(fā)學(xué)生強(qiáng)烈的認(rèn)知沖突,引導(dǎo)學(xué)生發(fā)現(xiàn)并提出問題:為什么除法豎式長得這么“怪”?從而討論出除法豎式如果像加法、減法、乘法豎式這么寫,余數(shù)便沒有位置寫。繼續(xù)討論,三行的豎式形式余數(shù)也可以有位置寫(直接寫在商的后面,中間用省略號隔開),再次引發(fā)學(xué)生的認(rèn)知沖突。當(dāng)學(xué)生“山窮水盡”之時(shí),通過簡單的分圓片,理解“我的15與你的15有什么不同”“哪個(gè)算式更像把45平均分成3份的意思”,使學(xué)生直觀地感悟豎式代表了除法的意義和過程的記錄,從而使學(xué)生理解45÷3=15的筆算過程便順理成章了。通過孩子自己的苦苦思辨,教師的巧妙引導(dǎo),此時(shí)此刻的學(xué)生一定有撥云見日、豁然開朗的感覺!
這也讓筆者回憶起二年級下冊開始教學(xué)《筆算除法》時(shí),學(xué)生存在這樣的疑惑,為什么除法豎式這樣寫,教師是否正面地回答?是否有采取通俗易懂的形式讓學(xué)生感悟?俞老師便做到了正視學(xué)生學(xué)習(xí)之惑,引發(fā)學(xué)生不斷地提出質(zhì)疑,發(fā)現(xiàn)問題,尋找緣由,引導(dǎo)孩子回到除法的意義,感悟數(shù)學(xué)的形式意義。
那么,除法豎式的第一次亮相又該以什么形式出現(xiàn)?怎樣教書寫的順序?這是每一位教過本節(jié)課教師的困惑。很多教師讓學(xué)生探究除法豎式怎么寫,學(xué)生絞盡腦汁創(chuàng)造出了許多寫法,最終還是聽教師“從頭道來”。如此探究,只是課堂上多了一種形式化的探究教學(xué)而已。而除法豎式的書寫形式是經(jīng)過了多年的多次完善的結(jié)果,讓學(xué)生去創(chuàng)造顯然是不切實(shí)際的。所以,筆者認(rèn)為用有意義的接受性學(xué)習(xí)方式是比較可取而高效的。
計(jì)算教學(xué)中算理與算法是一個(gè)不可分割的整體,算理是通過算法來表現(xiàn),算法又能體現(xiàn)出算理,算法的掌握應(yīng)該和算理的理解統(tǒng)一起來。當(dāng)學(xué)生積累了豐富的感性知識之后,通過對算理與算法的有效聯(lián)結(jié),充分體驗(yàn)到算理到算法的演變過程,對算理的理解就會更深刻,對算法的掌握更扎實(shí)。教師要尋求好算理與算法的平衡點(diǎn),使教學(xué)扎實(shí)又不失靈活。
2.準(zhǔn)確把握生長點(diǎn)與思考點(diǎn)
筆算除法教學(xué)中要注意在學(xué)生的各種算法中關(guān)注新知識的生長點(diǎn),在關(guān)鍵處及時(shí)追問,促進(jìn)學(xué)生知識的遷移。如教學(xué)《除數(shù)是整十?dāng)?shù)的筆算除法》一課。
師:商為什么寫在個(gè)位上?
生:3在十位上,表示30,30×30=900,已經(jīng)超過92了。
師:還有誰想說?
師:這里十位上9可不可以除以30,對嗎?那你們認(rèn)為9除以30夠除嗎?(不夠)所以除數(shù)是整十?dāng)?shù),我們先看被除數(shù)的前幾位?
生:前兩位。
師:這里我們除到了什么位?
生:個(gè)位。
師:那么,就要把商寫在……個(gè)位的上面。
學(xué)生容易從乘法的角度分析討論,此處教師應(yīng)勢利導(dǎo),抓準(zhǔn)筆算除法的關(guān)鍵點(diǎn),追問“十位上的9可不可以除以30”,為學(xué)生的后續(xù)探究提供了思路。
從而,以此為生長點(diǎn)教學(xué)后面的178÷30,多把講臺交給學(xué)生,引發(fā)學(xué)生暴露試商的過程,并與30×( )<178聯(lián)系起來,容易分析總結(jié)得出:除數(shù)是兩位數(shù)的除法,要看被除數(shù)的前兩位,前兩位不夠除,就要看被除數(shù)的前三位。不僅使全體學(xué)生學(xué)會了試商的技巧,還得出了計(jì)算法則。其次,筆者還發(fā)現(xiàn)部分學(xué)生對算法中“除到被除數(shù)的哪一位,就在那一位的上面寫商”不理解,因此,特別是在起始課中,教師還應(yīng)抓準(zhǔn)知識的生長點(diǎn)多讓學(xué)生說一說以鞏固算法。
教師還可充分利用課堂中的方法多樣化、錯(cuò)例等生成資源,引導(dǎo)學(xué)生思考探究。
出示:一個(gè)三位數(shù)除以兩位數(shù),要使商是一位數(shù),被除數(shù)最高位可以填幾?
師:你能找出所有的填法嗎?
(鼓勵(lì)學(xué)生思考,留給學(xué)生充分的思考時(shí)間。)
生1:被除數(shù)的最高位可以填1、2、3。
師:你是怎么想的?
生1:比如19除以40,十位上不夠商1,填2、3,十位上也不夠商1,所以商都是一位數(shù)。
師:只要怎么做就能保證商是一位數(shù)?
生2:只要被除數(shù)的前兩位比除數(shù)小,就能保證商是一位數(shù)。
生3(迫不及待):老師,我還有方法!
師:哦?說說看!
生3:商的位置上填9。
師(一愣,繼續(xù)追問):你是怎么算的?
生3:因?yàn)?×40=360,被除數(shù)的最高位最大是3,所以可以填1、2、3。
師:你們覺得她的方法怎么樣?
生4:我覺得她的方法挺方便的。
師:是呀,多么巧妙的方法啊!而且還根據(jù)商最大能填6,算出了被除數(shù)的最高位最大只能填3。
學(xué)生通過獨(dú)立思考、推理找到準(zhǔn)確答案,不僅提煉出了三位數(shù)除以兩位數(shù)商位數(shù)的數(shù)字特點(diǎn),還將乘法與除法進(jìn)行聯(lián)系,發(fā)散了學(xué)生的思維。教師在教學(xué)中應(yīng)努力創(chuàng)設(shè)真正適合學(xué)生思考的問題,使學(xué)生在交流中碰撞出思維的火花,引發(fā)學(xué)生創(chuàng)造出有價(jià)值的問題。
3.合理進(jìn)行比較總結(jié)與拓展提高
針對筆算除法方法的多變,在教學(xué)時(shí)應(yīng)該讓學(xué)生多比較,并加強(qiáng)當(dāng)堂練習(xí)。
(1)比較總結(jié)
每學(xué)一個(gè)新知識,就讓學(xué)生對新舊知識進(jìn)行比較,有什么不同點(diǎn)和相同點(diǎn),關(guān)于這些不同點(diǎn)、易混淆點(diǎn)如何區(qū)分、理解,這樣更有利于學(xué)生總結(jié)出新知識的特點(diǎn)和筆算方法。如教學(xué)“應(yīng)用商的變化規(guī)律”使筆算簡便的方法。
師:比較這兩種方法有什么相同點(diǎn)?
生1:商都一樣。
生2:都沒有余數(shù)。
生3:計(jì)算的結(jié)果都是一樣的。
師:有什么不同?
生1:一個(gè)不劃“0”,一個(gè)劃“0”。
生2:左邊的中間的過程和右邊的過程不同。
師:能說得更具體詳細(xì)些嗎?
生2:左邊的是60,右邊的是6,左邊的是180,右邊的是18。
師:為什么會出現(xiàn)這樣的差異?
生3:因?yàn)樽筮叺氖?乘30等于60,6乘30等于180,右邊的是2乘3等于6,6乘3等于18。
師:還有什么不同嗎?
生4:商的位置不同。
師:為什么商的位置會不同?
生5(迫不及待):因?yàn)樽筮叺氖窍人?8除以30,商2,寫在8的上面;右邊的是先算7除以3,商2,應(yīng)寫在7的上面。
師:你的意思是說除到哪一位……(商就寫在哪一位的上面)
生6:我還發(fā)現(xiàn)了最后那個(gè)“0”的位置也不同。
師:哦?這又是怎么回事?
生6:因?yàn)樽筮叺氖?80減180,“0”當(dāng)然寫在“0”的下面,右邊的是算18減18,0自然就寫在8的下面了。
師:關(guān)于這種被除數(shù)和除數(shù)末尾都有零的筆算方法,你想提醒同學(xué)們什么?
生:……
師:那么下面兩種方法又有什么不同?(出示學(xué)生計(jì)算過的840÷50的兩種筆算方法)
生:……
學(xué)生在比較中對算理和算法有了更全面的認(rèn)識。
(2)多進(jìn)行當(dāng)堂練
運(yùn)算能力是在不斷地運(yùn)用數(shù)學(xué)概念、法則、公式,經(jīng)過一定數(shù)量的練習(xí)而逐步形成的。本文所闡述的“練”,不是教師出題讓學(xué)生做的機(jī)械練習(xí),而是在學(xué)生比較總結(jié)出這節(jié)課算式的特點(diǎn)后,讓他們自己照樣子創(chuàng)造同類型的題目,再進(jìn)行練習(xí)。學(xué)生在創(chuàng)造中一次又一次總結(jié)這些算式的特點(diǎn),這樣的教學(xué)更有利于學(xué)生對算理及算法的理解和掌握。
筆算除法教學(xué)中,教師應(yīng)堅(jiān)持“以學(xué)定教”,一切從學(xué)生的角度看問題,充分暴露學(xué)生的原有水平,根據(jù)學(xué)情有針對性地設(shè)計(jì)教學(xué),“從學(xué)生中來,到學(xué)生中去”,呈現(xiàn)給學(xué)生利于建構(gòu)的學(xué)習(xí)材料,讓學(xué)生感覺到其實(shí)筆算除法離自己很“近”,很“真實(shí)”,真正觸動(dòng)學(xué)生的內(nèi)心需求、撥動(dòng)學(xué)生的心弦,這樣才能讓筆算除法教學(xué)做得更加合理、高效。
(作者單位:浙江省樂清市丹霞路小學(xué))

