R軟件在正態總體假設檢驗教學中的應用探討

◎郭朝會

(重慶師范大學數學科學學院，重慶 401331)

R軟件在正態總體假設檢驗教學中的應用探討

◎郭朝會

(重慶師范大學數學科學學院，重慶 401331)

本文介紹了R軟件在正態總體假設檢驗教學中的一些應用.通過教學實例闡述如何利用R軟件進行直觀教學，提高學生對假設檢驗原理的理解，從而培養學生的學習興趣以及提高學生探索問題、解決問題的能力.

數理統計；假設檢驗；R軟件

一、前 言

數理統計[1，2]是理工科高等院校的基礎必修課程，在高等教育課程中占有舉足輕重的地位.假設檢驗作為統計推斷的三大內容之一，貫穿于數理統計學的始終.因此，它在數理統計這門課程中占有非常重要的位置.如何提高假設檢驗的教學，讓學生深刻理解假設檢驗的統計原理是數理統計教學的重點和難點.而傳統的教學方法，很難形象直觀地展現假設檢驗的統計原理，使得學生對假設檢驗原理的理解有一定的難度.隨著現代科技的飛速發展，許多現代教學手段可以運用到學生學習以及教師教學中來.最流行的方法之一就是使用教學軟件來輔助教學，展現統計的思想和方法，提高統計教學的效率.目前應用最廣泛的教學軟件工具無疑是MATLAB、SPSS、SAS等商業軟件.由于在大學教育中我國越來越重視知識產權，因此，教學單位若想將上述商業軟件應用于日常教學，必須有足夠的經費支持.然而，這對于自主學習的學生或教師來說帶來了一定的困難.R軟件是由奧克蘭大學統計學系的Ross Ihaka和Robert Gentleman共同創立，它功能強大、操作簡單，更重要的是它是一款完全免費的統計分析軟件.R軟件提供了有彈性的、互動的環境來分析和展示數據，它一般用于統計建模、統計計算、數據處理等.R軟件還有一項很重要的功能，就是它包含了許多有用的程序包，到目前為止，R軟件官方網站就已經提供了超過七千個程序包，涵蓋數理統計學、金融統計學、生物統計、經濟管理、社會學等.其次，通過加載這些程序包可以讀取源代碼，并可以根據自己的需求改寫其源代碼得到適合新問題的程序.因此，相比于商業軟件，R軟件在數據分析和統計建模等方面毫不遜色.因此，正是由于R軟件的獨特之處使得它特別適合輔助數理統計教學[3，4].

在實際問題中大多數數據都服從或近似服從正態分布，所以，本文重點考慮如何利用R軟件實現單個正態總體均值的假設檢驗直觀教學以及提高學生動手操作的能力.

二、R軟件在單個正態總體均值假設檢驗中的應用

首先，我們回顧一下單個正態總體均值假設檢驗的統計理論.根據假設檢驗思想：若原假設成立導致了不合理的現象發生，則我們就應該拒絕原假設否則接受原假設，即通過限制犯第一類錯誤的概率來求得拒絕域.設X1，…，Xn是來自N(μ，σ2)的一組獨立同分布樣本，現我們考慮如下的雙邊檢驗問題H0：μ=μ0，H1：μ≠μ0.

① 若方差σ2已知，因此，根據假設檢驗的思想，我們有

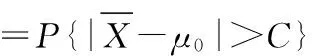
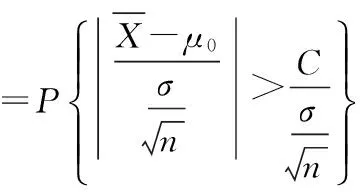
(1)

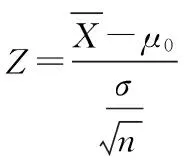
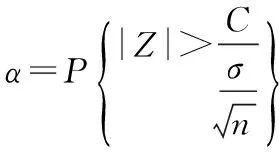
(2)

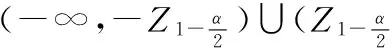
② 若方差σ2未知，統計量Z中包含未知參數σ，因此，需要構造新的統計量.根據抽樣分布定理，我們可知

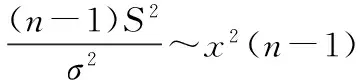
再由t分布的定義知

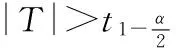
下面我們通過一個例子來闡述單個正態總體均值的假設檢驗問題.

例1[5]正常男子血小板計數均值為225×109/L，今測得20名男性油漆作業工人的血小板計數值(單位：109/L)如下：220，188，162，230，145，160，238，188，247，113，126，245，164，231，256，183，190，158，224，175，問油漆工人的血小板計數與正常成年男子有無差異？

解 根據題意需檢驗

H0：μ=μ0=225，H1：μ≠μ0.

我們首先需要判定此組數據是否來自于正態分布，因此，我們采用Shapiro-Wilk(夏皮羅-威爾克)W統計量做正態性檢驗，相應理論可參考文獻[5].在R軟件中可用shapiro.test命令來做檢測，檢測結果如下：

shapiro.test(x)#x代表此組數據所構成的向量

Shapiro-Wilk normality test

data：x

W=0.95063，p-value=0.3768

根據結果可知p-value=0.3 768>α=0.05，則可判定此組樣本來自于正態總體.又因為此組數據的方差未知，因此，采用t檢驗.針對這個檢驗問題本文編寫了一個程序來實現，相應的代碼和結果如下：

##編寫的單個正態總體均值假設檢驗的代碼

normal.mean.test=function(x，mu0，sigma，alpha){

#x樣本觀測值；mu0均值；sigma標準差；alpha顯著性水平

n=length(x)#待測樣本個數

x.mean=mean(x)#計算樣本的均值

if(sigma=="known"){#判定總體方差是否已知，若已知則做如下命令

Z=(x.mean-mu0)/(sigma/sqrt(n))#計算Z統計量

result=abs(Z)>qnorm(1-alpha)#計算拒絕域

if(pnorm(Z)<0.5){p.value=2*pnorm(Z)}else{

p.value=2*(1-pnorm(Z))}#計算p值

if(result=="TRUE")print("拒絕原假設")

list(Z=Z，p.value=p.value)#輸出結果

}else{#總體方差未知，做如下命令

x.var=sd(x)#計算樣本標準差

T=(x.mean-mu0)/(x.var/sqrt(n))#計算T統計量的值

if(pt(T，n-1)<0.5){p.value=2*pt(T，n-1)}else{

p.value=2*(1-pt(T，n-1))}#計算p值

result=abs(T)>qt(1-alpha，n-1)##計算拒絕域

if(result=="TRUE")print("拒絕原假設")

list(T=T，p.value=p.value)#輸出結果 }}

normal.mean.test(x，mu0=225，sigma="unknown"，alpha=0.05)##調用所編寫的函數結果如下：

[1]"拒絕原假設"

$T

[1]-3.478262

$p.value

[1]0.002516436

一方面，從第一條結果可知我們應該拒絕原假設，即油漆工人的血小板計數與正常成年男子有顯著差異.另一方面，在顯著性水平是α=0.05的情況下，p-value=0.002 516 436<α=0.05，此結果也說明應該拒絕原假設.另外，在R軟件中可以利用命令t.test來檢驗方差未知的正態總體的均值檢驗，針對此例題調用t.test函數結果如下：

t.test(x，alternative="two.sided"，mu=225)

One Sample t-test

data：x

t=-3.4783，df=19，p-value=0.002516

alternative hypothesis：true mean is not equal to 225

95 percent confidence interval：

172.3827 211.9173

sample estimates：

mean of x 192.15

此結果跟我們編寫normal.mean.test函數所得結果一致，即油漆工人的血小板計數與正常成年男子有顯著差異.

三、總 結

目前數理統計教學的理論抽象、公式復雜，因此，很多學生在學習這門課程時存在很多問題，尤其對于假設檢驗這一節的內容.如能將R軟件引入假設檢驗的教學中，不僅可以加深學生對假設檢驗知識的理解，還可以使學生擺脫煩瑣的計算，從而很大程度上提高了學生處理數據的能力.本文結合實例，介紹了R軟件在單個正態總體的均值假設檢驗中的具體應用.首先，R軟件能夠直觀地畫出統計量的密度函數曲線圖，從而高效地解決假設檢驗中很多教與學的問題.其次，R軟件給我們提供了很多經典的統計命令(如本文介紹的shapiro.test、t.test等)，通過直接調用就能獲得相應的統計分析結果.最后，當代教師不僅要會講授教材上的理論知識，還需利用統計軟件將理論知識與實踐相結合，從而促進教師自身的學術造詣和實踐教學能力的提升.

[1]孫榮恒.應用數理統計(第二版)[M].北京：科學出版社，2003.

[2]劉瓊蓀，鐘波，榮騰中，李曼曼.概率論與數理統計[M].北京：高等教育出版社，2014.

[3]趙軍，楊琳.R軟件在大學數學教學中的應用探討[J].高教學刊，2016(7):93-95.

[4]程勝.R統計軟件及其在《時間序列分析》實踐教學中的應用[J].教育教學論壇，2014(41):173-175.

[5]薛毅，陳立萍.統計建模與R軟件[M].北京：清華大學出版社，2007.

重慶師范大學基金項目資助(16XLB019).