柱殼法求解旋轉體體積
2017-06-01 11:29:56董愛君徐大舉
數學學習與研究 2017年9期
關鍵詞:區域
◎董愛君 徐大舉
(山東交通學院,山東 濟南 250357)
柱殼法求解旋轉體體積
◎董愛君 徐大舉
(山東交通學院,山東 濟南 250357)
柱殼法在求解旋轉體體積中具有重要應用,它不僅適用于旋轉軸為坐標軸或與坐標軸平行的直線的情形,對于旋轉軸為任意斜直線時,也同樣適用,本文對于后者進行了討論.
柱殼法;旋轉體;軸型區域
柱殼法是一種重要的求解旋轉體體積的方法,下面,我們來研究旋轉軸為斜直線的情況,為了方便,給出如下定義.
定義1 軸型區域:如果一個平面區域D滿足以下兩個條件:(1)平行于旋轉軸的直線l穿過區域D時,直線l與區域D的邊界至多有兩個交點;(2)區域D的其中一條邊界為垂直于旋轉軸的直線上的線段,則稱它為軸型區域.
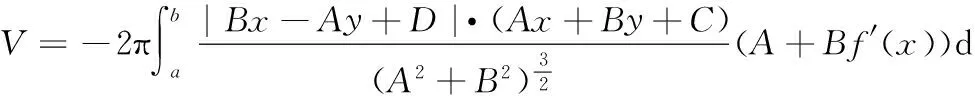
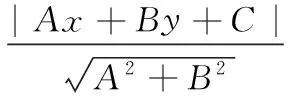
ΔV=πd2h-πd′2h
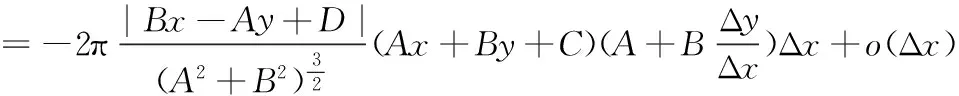

舉例如下:
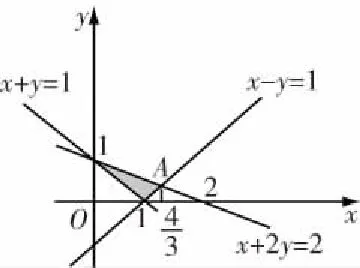
圖2
例1 求由直線L1:x+y=1,直線L2:x-y=1及直線L3:x+2y=2所圍成的區域(圖2陰影部分)繞直線L2:x-y=1旋轉一周得到的旋轉體的體積.
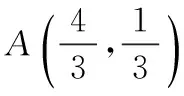

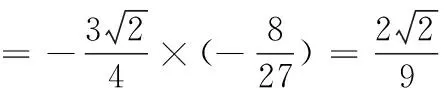

圖3
例2 求由直線L1:x+y=1,直線L2:x-y=1及圓弧L3:x2+y2=1所圍成的區域(圖3陰影部分)繞直線L2:x-y=1旋轉一周得到的旋轉體的體積.
可得A=1,B=-1,C=-1,D=1,且|Bx-Ay+D|=|-x-y+1|=x+y-1.從而,

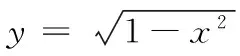

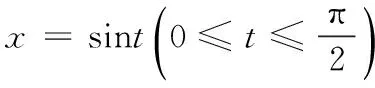
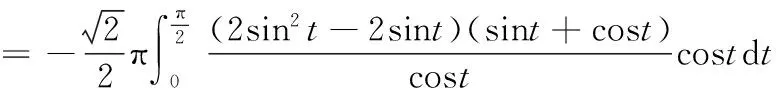

猜你喜歡
發明與創新·小學生(2021年3期)2021-03-25 11:48:49
科學(2020年5期)2020-11-26 08:19:22
軟件(2020年3期)2020-04-20 01:45:18
商周刊(2018年15期)2018-07-27 01:41:20
敦煌學輯刊(2018年1期)2018-07-09 05:46:42
北京教育·普教版(2017年1期)2017-02-05 13:26:23
新疆農墾科技(2016年2期)2016-08-21 13:50:16
中國科技博覽(2016年2期)2016-04-25 20:32:39
小學生導刊(2016年34期)2016-04-11 00:49:44
新疆財經大學學報(2015年3期)2015-12-10 03:49:15

