巧妙變換來解題

陳正亮

巧妙變換來解題

陳正亮

初中圖形變換包含平移、翻折和旋轉，在幾何解題中，要把握變換的本質，在圖形的運動中找到不變量，然后解決問題.變換的本質是使原有圖形的性質得以保持，改變其位置，使其轉化成新的有利于我們論證解答的幾何圖形.下面我們一起來看一下具體問題.

例1 已知：如圖1，在△ABC中，AB=5，AC=3，求中線AD的范圍.

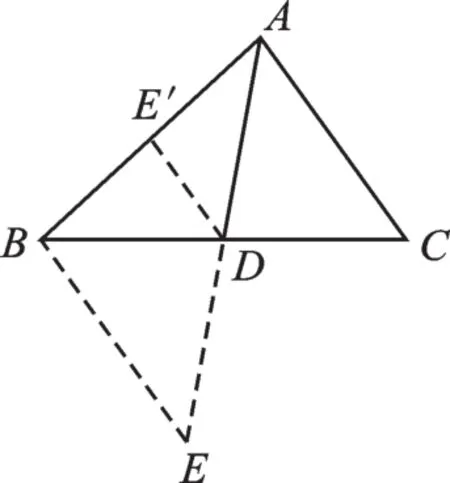
圖1

【分析】采用倍長中線的方法，可以將△ADC繞點D旋轉180°，構造與之全等的三角形，然后利用“三角形兩邊之和大于第三邊”可解.當然也可以考慮在邊AB或AC上取中點，構造中位線，再用三角形三邊的性質解得.（請同學們自行完成，答案：1＜AD＜4）

變式練習1 如圖2，在△ABC中，D為BC的中點，AB=13，AD=6，AC=5.請猜想AD與AC的位置關系，并給出證明.（可以用兩種思路去考慮一下）

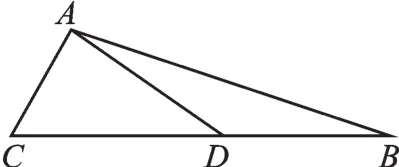
圖2

【小結】條件里面有中線，即可聯想到利用中位線來轉化相應的已知條件，或者倍長中線，將它們集中在一個三角形中，從而找出三條邊長之間的聯系.

例2 已知：如圖3，在正方形ABCD中，E為BC上的一點，F為CD上一點，且BE+DF= EF.求∠EAF的度數.

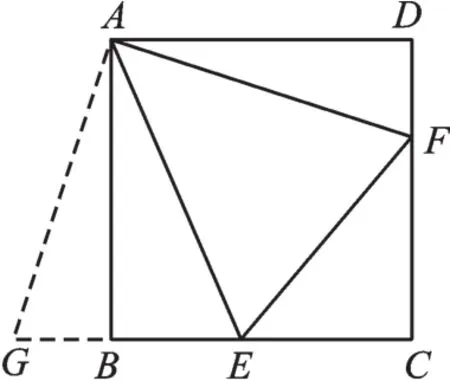
圖3

【分析】將△ADF繞點A順時針旋轉90°得到△ABG，然后再利用“SSS”證明△AEG≌△AEF.

變式練習2 如圖3，在正方形ABCD中，∠EAF=45°，E、F分別在BC與CD上.求證:EF= BE+DF.

【小結】利用正方形的邊長相等，通過旋轉一定的度數，把兩條線段集中到同一條線段上（補短法），再由相應的三角形全等證得結論.變式實際上與例題2屬于互逆命題，請同學們注意認真體會，今后解題往往能事半功倍，舉一反三.

例3 如圖4，△ABC是邊長為3的等邊三角形，△BDC是等腰三角形，且∠BDC=120°，以D為頂點作一個60°角，使其兩邊分別交AB于點M，交AC于點N，連接MN，則△AMN的周長為______.

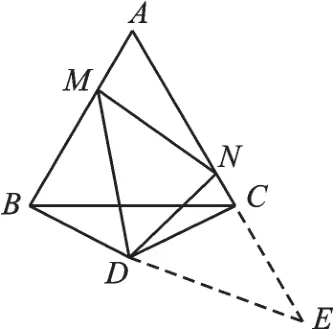
圖4

解：在AC的延長線上截取CE=BM，連接DE.

∵△ABC為等邊三角形，△BCD為等腰三角形，且∠BDC=120°，

∴∠MBD=∠MBC+∠DBC=60°+30°=90°，

∠DCE=180°-∠ACD=180°-∠ABD=90°，

在△CDE和△BDM中，

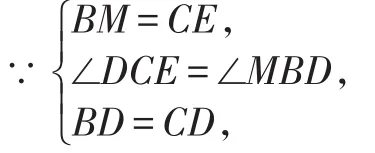
∴△CDE≌△BDM（SAS），

∴∠CDE=∠BDM，DE=DM，

∠NDE=∠NDC+∠CDE=∠NDC+∠BDM=∠BDC-∠MDN=120°-60°=60°，在△DMN和△DEN中，

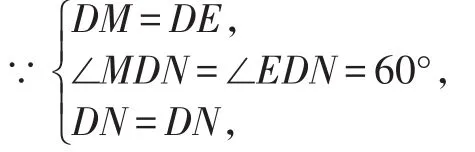
∴△DMN≌△DEN（SAS），

∴MN=NE=NC+CE=NC+BM，

△AMN的周長=AN+MN+AM=AN+NC+ BM+AM=AB+AC=6.

【小結】通過圖形補全構造全等三角形，利用的思維模式是全等的“平移”和“翻轉折疊”.

例題4 如圖5，已知∠BAC=45°，AD⊥BC于點D，且AD=6，CD=3.求BD的長.

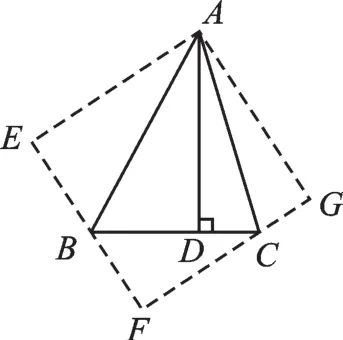
圖5

【分析】本題的已知條件中有個45°的角，我們可以考慮把45°的角轉化到等腰直角三角形或者正方形中去.解題方案中有多種利用相似形或者解直角三角形來處理的方法.在這里介紹一種比較巧妙的方法.通過將Rt△ABD和Rt△ACD分別向外作軸對稱圖形，可以自然構造出正方形AEFG，而正方形的邊長就是高AD=AE=EF=AG=FG=6.設BD=x，則BF=6-x.由對稱變換可以得到BE=BD，CG=CD，在Rt△BCF中，由勾股定理得（6-3）2+（6-x）2=（3+x）2，解得：x=2，即BD=2.（解答過程略）

變式練習3 如圖6，在平面直角坐標系xOy中，已知點A（4，0），B（-6，0），點C是y軸上的一個動點，當∠BCA=45°時，點C的坐標為______.友情提醒：坐標點C有兩個位置（0，12）和（0，-12）.

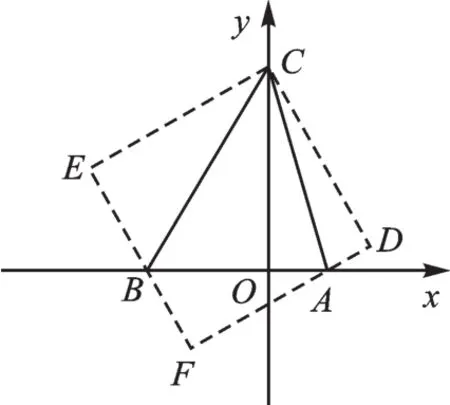
圖6

【小結】重點考查了45°角與90°角之間的關系，利用構造正方形這個特殊的基本圖形來解決，類似的一些問題還有對30°角與60°角的考查，半角或倍角關系等.

總之，幾何學研究圖形的形狀、大小及位置，而在初中階段對圖形位置問題的研究中，常見的變換問題占了很重要的一塊，希望同學們多加體會.

（作者單位：江蘇省常州市金壇區華羅庚實驗學校）