提煉結論創新應用
——圓錐曲線中弦的斜率與中點坐標關系的探究

李紅玲●

提煉結論創新應用
——圓錐曲線中弦的斜率與中點坐標關系的探究

湖北省孝感市湖北航天高級中學(432100)

李紅玲●

圓錐曲線是高考的重要考點之一，盡管教材和教學大綱主要強調的是通性通法，但由于圓錐曲線問題按通性通法處理往往運算量較大，過程繁瑣，不易算對，所以根據圓錐曲線的常見問題總結反思，適當提煉一些實用的結論，可大大簡化過程、減小運算量，特別是解選擇填空題，運用這些結論解題可取得事半功倍的效果.下面根據圓錐曲線的常見問題探究弦的斜率與中點坐標的關系，提煉出幾個結論供大家參考.

結論1 若直線l：y=kx+m(m≠0)與曲線(橢圓或雙曲線)Ax2+By2=1相交于P、Q兩點,弦PQ的中點為M(xm,ym)，則弦的斜率與中點坐標有如下關系：

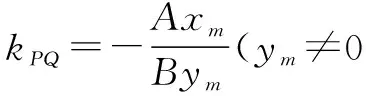
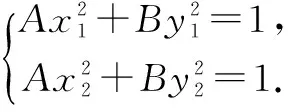
A(x1+x2)(x1-x2)+B(y1+y2)(y1-y2)=0，即2Axm(x1-x2)+2Bym(y1-y2)=0.

當ym=0時，若x1=x2，則PQ⊥x軸，kPQ不存在，與條件不符，故x1≠x2，則xm=0，直線l過原點，m=0，這與條件“m≠0”矛盾，從而ym≠0.所以

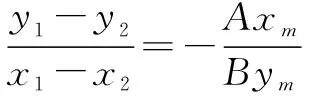
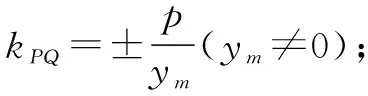
在結論1中，為了使結論簡潔、統一好記，使用了橢圓和雙曲線的統一方程Ax2+By2=1，而不是用a,b表示的標準方程，其中當A>0,B>0，且A≠B時，方程表示橢圓，當AB<0時表示雙曲線，故結論1對中心在原點，以坐標軸為對稱軸的橢圓和雙曲線均可使用，結論2對于拋物線的四種形式的標準方程都可以使用.使用這些結論解決圓錐曲線中與中點弦相關的問題比傳統方法要簡便快捷，下面舉例說明這些結論的應用.

應用1 求圓錐曲線被某點平分的弦所在直線方程

例2 求拋物線y2=4x被點(2,1)平分的弦所在直線的方程.

應用2 求圓錐曲線中平行弦中點的軌跡

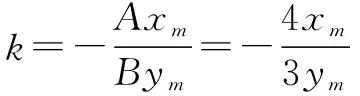
例4 求拋物線x2=4y中斜率為1的平行弦中點的軌跡.

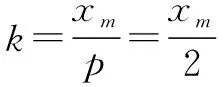
應用3 已知圓錐曲線的弦被某點平分，求圓錐曲線的方程

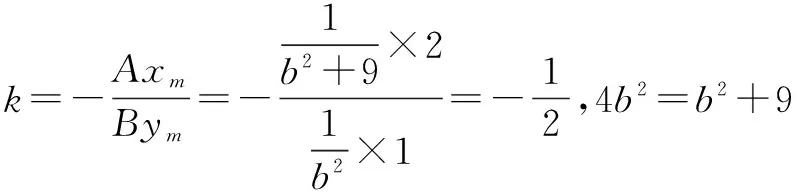
事實上，提煉結論并靈活運用是把常規方法中的很多繁瑣而重復的過程加以省略.從而提高解題效率的一種有效做法，也是培養學生進行研究性學習并品嘗研究成果的一種很好的方式.

G632

B

1008-0333(2017)01-0048-01