考慮定子鐵芯和繞組各向異性的爪極發電機模態分析

鄧文哲， 左曙光， 孫 罕， 吳雙龍， 張國輝

(1.同濟大學 新能源汽車工程中心，上海 201804； 2.上海法雷奧汽車電器系統有限公司，上海 201201)

考慮定子鐵芯和繞組各向異性的爪極發電機模態分析

鄧文哲1， 左曙光1， 孫 罕2， 吳雙龍1， 張國輝1

(1.同濟大學 新能源汽車工程中心，上海 201804； 2.上海法雷奧汽車電器系統有限公司，上海 201201)

為了分析車用爪極發電機的固有特性，對爪極發電機進行了模態試驗和有限元分析。首先對發電機定子鐵芯和定子總成進行模態試驗，獲取了其模態振型和模態頻率；根據定子鐵芯與繞組的有限元等效模型和獲取的模態參數，識別出鐵芯和繞組的等效各向異性材料參數；其次考慮各零部件之間復雜的連接關系，建立了發電機整機的自由模態有限元模型，自由模態試驗表明該模型具有較高的準確性；最后在自由模態模型的基礎上建立了發電機約束模態有限元模型，并進行了振動試驗。自由模態試驗和振動測試結果表明，綜合考慮定子鐵芯和繞組的各向異性材料特性和螺栓預緊力等因素能夠準確預測爪極發電機的模態特性，為爪極發電機振動與噪聲的數值預測和減振降噪研究奠定了基礎。

爪極發電機；模態分析；各向異性；螺栓預緊力；振動

爪極發電機由于其工藝簡單、成本低并且功率密度較大等優點，在汽車上得到了廣泛的應用。隨著發動機的噪聲逐漸得到了抑制，爪極發電機的振動與噪聲逐漸成為了一個突出問題，受到了生產廠家和用戶的密切關注[1-2]。為了實現爪極發電機振動噪聲的數值預測的減振降噪，需要建立能夠準確預測其模態參數的有限元模型。對于發電機整機而言，零部件模型的準確建立和連接關系的準確模擬是影響有限元模型精度的重要因素[3]。

在電機各零部件的建模中，端蓋等實體結構通過有限元軟件一般可以準確計算其模態特性，而對于定子鐵芯和繞組這種非實體部件，由于結構的特殊性，其結構的等效和材料參數的獲取一直是模態分析的難點和熱點。早期的一些研究通常只考慮繞組質量對定子系統固有頻率的影響，在建模時繞組以附加質量的形式施加在模型中[4-5]。但是研究表明與定子鐵芯緊密接觸的繞組對電機模態的影響不僅是附加質量作用，還有剛度效應[6-7]。因此一些學者在建模時同時考慮了繞組質量和剛度，建立了定子鐵芯和繞組的等效模型。文獻[8]對爪極發電機的定子進行了模態分析，在建模時將繞組簡化為直導體，忽略了繞組端部的影響。文獻[9]在對異步電機進行模態分析時，同樣將繞組簡化為直導體。上述文獻在建模時均對鐵芯和繞組賦予了各向同性材料參數，但是對于實際的定子鐵芯和繞組，它們并非實體結構，導致其材料參數表現出明顯的正交各向異性，這就給模型的準確性帶來了一定的誤差。文獻[10]在建模時考慮了繞組的各向異性材料參數，但認為鐵芯的材料參數是各向同性的，同時未給出獲取各向異性材料參數的一般性方法。文獻[11]則通過超聲波脈沖試驗測定了開關磁阻電機定子的材料參數，該方法可以直接獲取材料參數，但是對于試驗條件的要求以及成本都比較高。綜合上述文獻可知，目前綜合考慮定子鐵芯和繞組的各向異性材料參數的相關研究相對較少，同時也缺乏快速有效的方法對其各向異性參數加以識別，這對準確建立定子系統的有限元模型帶來了一定的困難。

實際的爪極發電機是一個復雜的裝配體，周期性變化的電磁力作用在定子齒面，引起定子振動并通過端蓋向外輻射噪聲，因此需要考慮整個裝配體的模態特性，才能對其振動與噪聲特性進行預測分析。電機各零部件之間連接關系的模擬對于準確建立發電機整機的有限元模型具有重要的影響。文獻[12]對車用發電機進行了模態分析，各零部件之間通過部分節點耦合的方式建立剛性連接，模型簡化較多。本文在建模時將重點從螺栓預緊力和零部件之間的接觸設置等幾個方面進行考慮。

綜上所述，本文首先對定子鐵芯和定子總成進行模態試驗，并識別出定子鐵芯和定子總成的模態參數，包括其模態振型和模態頻率。根據建立的定子鐵芯和繞組的有限元等效模型和獲取的模態參數，識別出鐵芯和繞組的等效各向異性材料參數。之后運用獲取的材料參數，建立了考慮復雜連接關系的發電機整機自由模態有限元模型，自由模態試驗表明該模型具有較高的準確性。最后在自由模態模型的基礎上建立了發電機約束模態有限元模型，并通過振動試驗加以驗證。模態分析主要流程，如圖1所示。自由模態試驗和振動測試結果表明，該模型可以準確的反映爪極發電機整機的固有模態，為爪極發電機振動與噪聲的數值預測和減振降噪研究奠定了基礎。

1 爪極發電機結構

爪極發電機主要是由定子、轉子、前后端蓋、散熱風扇以及整流元件等部件組成。定子由定子鐵芯和電樞繞組組成，勵磁繞組通過支架繞制在轉子磁軛上，前后端蓋通過螺栓對定子進行夾緊，轉子通過軸承支撐在前后端蓋上，整流元件安裝在后端蓋的外側，發動機通過皮帶輪帶動發電機進行工作。其結構，如圖2所示。

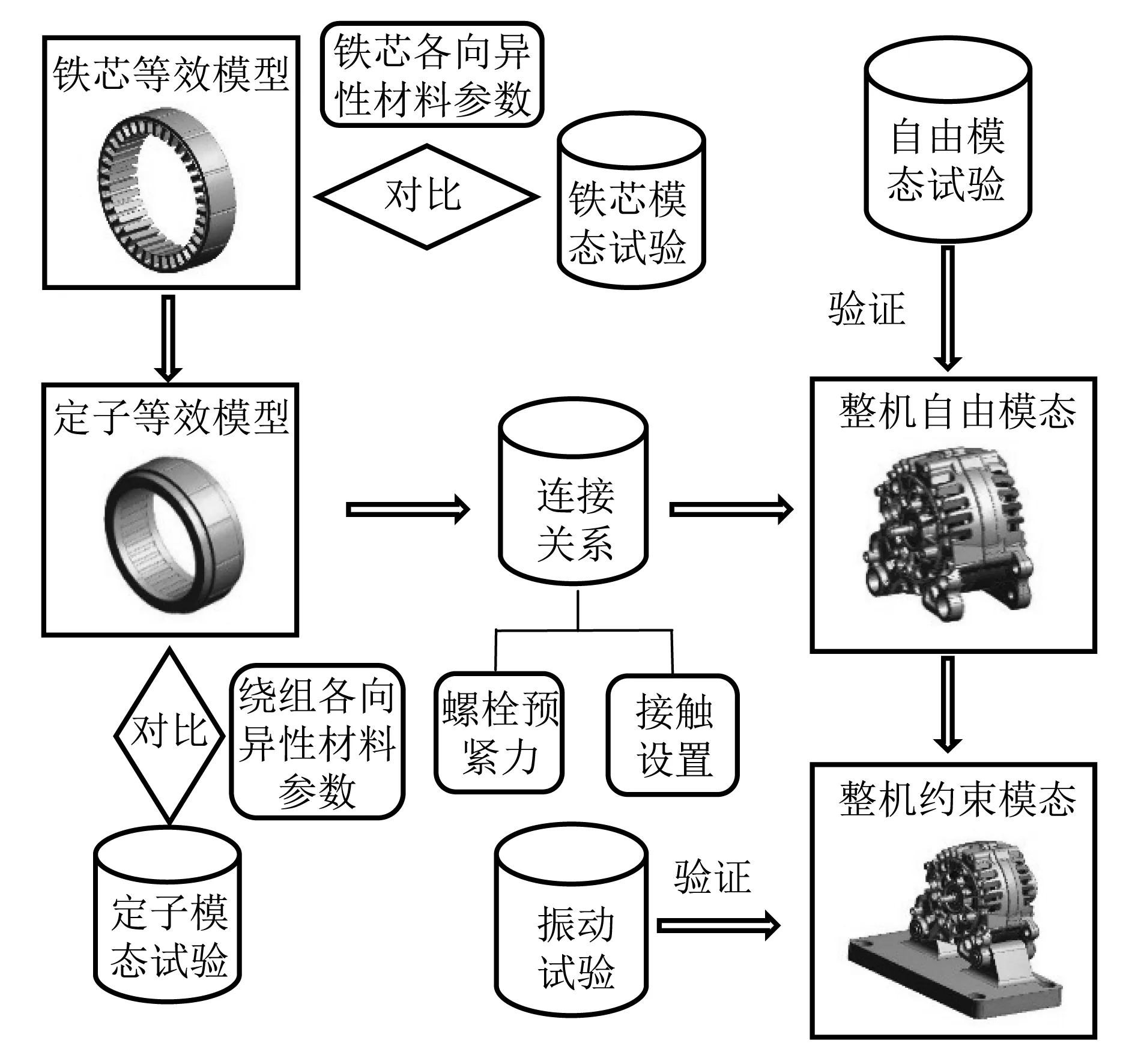
圖1 爪極發電機模態分析流程Fig.1 Modal analysis procedure of claw-pole alternator

圖2 爪極發電機結構圖Fig.2 Exploded view of claw pole alternator

2 定子鐵芯和繞組的各向異性建模

2.1 定子鐵芯和定子總成模態試驗

定子鐵芯和繞組并不是連續的彈性介質，定子鐵芯是由硅鋼片沿著軸向進行堆疊得到，繞組是由導線繞制在定子齒上，這就導致其材料參數并不等于實際的硅鋼和銅的材料參數，表現出較為明顯的正交各向異性，而這種各向異性的材料參數的獲取也一直是電機定子系統準確建模的難點。為了獲取定子鐵芯和繞組的各向異性材料參數，建立準確的有限元模型，本文首先對定子鐵芯和定子總成進行了模態試驗。

目前電機模態試驗的分析方法主要有錘擊法和激振器法。錘擊法采用多點激振單點拾振的方法，操作比較簡單，但是該方法對敲擊技術要求較高，很難保證每次敲擊的位置和力度，并且激勵力的頻率范圍難以控制，導致其高頻模態難以被激發。而激振器法由于采用單點激振多點拾振的方法，可以保證激振位置，并且激勵可控。因此本文采用激振器法進行模態試驗。

定子鐵芯和定子總成模態測試現場，如圖3所示。定子沿徑向發生變形，因此激振器沿徑向進行激勵。試驗時沿圓周每圈布置了16個徑向振動測點，同時為了識別其軸向模態沿軸向共布置2圈，共計32個測點。由于定子軸向階數等于1的模態振型的節點在軸向中間位置，在選擇激振位置時應避開此位置，如圖4所示。其余測點為拾振位置。

圖3 定子鐵芯和定子總成模態測試現場圖Fig.3 Modal test of stator core and stator assembly

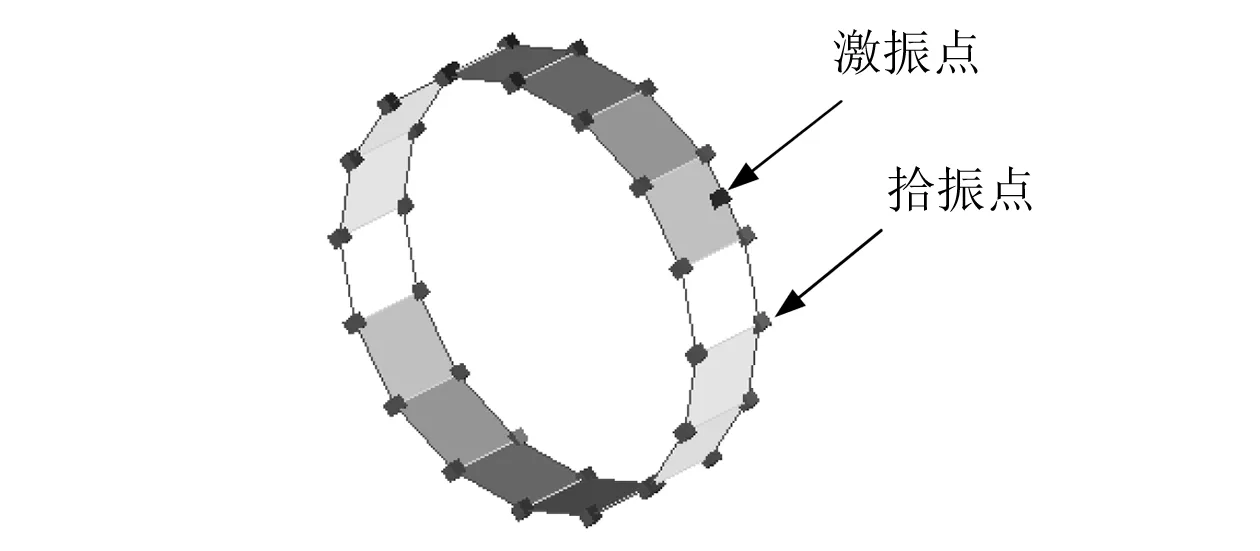
圖4 激振點和拾振點Fig.4 Exciting and detecting point

根據試驗獲取了定子鐵芯和定子總成5 000Hz以內的模態頻率和模態振型，如表3、圖6和圖7所示。其中m表示軸向節點數，n表示徑向節點數。當m=0時，定子沿軸向振動相位一致，當m=1時，定子軸向兩端振動相位相反。由于該定子的長徑比比較小，只識別出部分軸向節點為1的模態參數。

2.2 定子鐵芯和繞組模型等效

電機定子由定子鐵芯和繞組兩部分組成。為了建立較為準確的定子有限元模型，在建模時對定子鐵芯和繞組采用了如下方式進行等效：

(1)定子鐵芯采用實體結構進行建模，其層疊特性通過各向異性材料參數加以考慮。鐵芯的密度等于其實際的質量與其體積的比值。

(2)由于該電機采用分布繞組，端部較長，在建模時不能忽略繞組端部對定子模態的影響。實際的繞組形式過于復雜，在建模時對槽內和端部的繞組加以簡化，將繞組端部簡化為空心圓柱體，槽內繞組簡化為直導體。繞組的密度同樣取其實際的質量與體積之比，層疊特性通過各向異性材料參數加以考慮。

建立的定子鐵芯和繞組等效模型，如圖5所示。

2.3 定子鐵芯和繞組各向異性材料參數獲取

定子鐵芯和繞組均非實體結構，由于在有限元等效模型中采用了實體模型，因此必須將實體賦予各向異性材料參數來體現層疊結構的影響。材料的正交各向異性材料參數一般包括x，y，z方向的楊氏模量(Ex，Ey，Ez)和xy，yz，xz平面內的剪切模量(Gxz，Gyz，Gxy)。鐵芯是由硅鋼片沿著軸向(z向)進行堆疊，繞組由導線沿著徑向和切向(x和y向)進行堆疊，這就導致鐵芯和繞組軸向(z向)的材料特性明顯不同于x和y方向的材料特性，而由于結構的對稱性一般認為x和y方向的材料特性是相同的。因此鐵芯和繞組在x和y方向具有相同的楊氏模量，在xz和yz平面具有相同的剪切模量，即Ex=Ey，Gxz=Gyz，則鐵芯和繞組在x，y，z方向的楊氏模量和xy，yz，xz平面內的剪切模量只有四個參數是獨立的。通過有限元軟件對材料參數進行參數化分析可以發現，Ex(Ey)，Gxy的變化對m=0的模態參數影響較大，Gxz(Gyz)對m=1的模態參數影響較大，而Ez對于模態頻率幾乎沒有影響。

圖5 定子有限元模型Fig.5 FE model of stator

首先對定子鐵芯的各向異性材料參數進行了獲取。根據上述規律，通過修正定子鐵芯等效模型的Ex(Ey)，Gxy值，使m=0的模態仿真與試驗結果相一致，接著修正Gxz(Gyz)，使m=1的模態仿真結果逼近試驗結果。最終獲取了定子鐵芯的各向異性材料參數，如表1所示。其中，ρ為密度；v為泊松比；E為楊氏模量；G為剪切模量。

表1 定子鐵芯各向異性材料參數Tab.1 Orthotropic parameters of stator core

其次獲取了繞組的各向異性材料參數。根據表1獲取的定子鐵芯的材料參數，可以準確建立定子鐵芯的有限元模型。同樣地，通過修正定子總成等效模型中繞組的Ex(Ey)，Gxy值，使定子總成m=0的模態仿真與試驗結果相一致，接著修正Gxz(Gyz)，使m=1的模態仿真結果逼近試驗結果。最終獲取了繞組的各向異性材料參數，如表2所示。

表2 繞組各向異性材料參數Tab.2 Orthotropic parameters of winding

根據表1和表2獲取的定子鐵芯和繞組的各向異性材料參數建立的定子有限元模型的計算結果與試驗對比，如表3所示。定子徑向模態振型，如圖6所示。從左至右依次為試驗、定子鐵芯和定子總成有限元計算獲取的振型。圖7為試驗獲取的m=1時的模態振型和相對應的有限元結果。

由表3可知，繞組的存在使得定子總成的二階和三階模態頻率相對于定子鐵芯有所增加，四階和五階模態頻率出現一定的下降。這說明繞組在低階模態主要表現出剛度效應，使定子系統的剛度有所增加，隨著模態頻率的增加，質量效應逐漸占據主導地位，定子系統的模態頻率反而出現下降，因此在定子系統建模時需要同時考慮繞組質量和剛度的影響。同時定子鐵芯和定子總成的仿真與試驗結果的誤差均在3%以內，說明通過考慮定子鐵芯和繞組各向異性材料參數可以準確建立定子系統的等效模型，該模型可以用于整機的有限元建模。

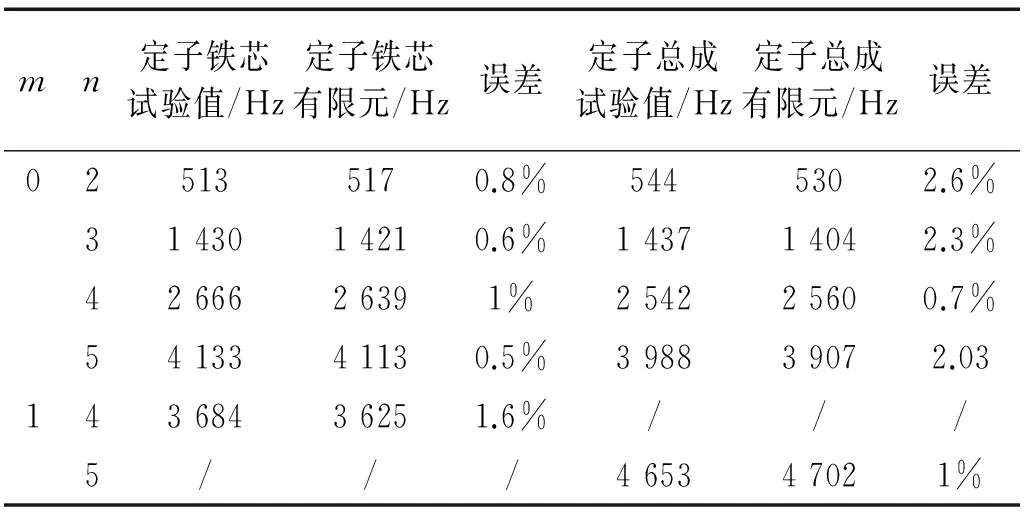
表3 定子模態頻率試驗與有限元結果對比Tab.3 Comparison between tested results and calculated results of stator

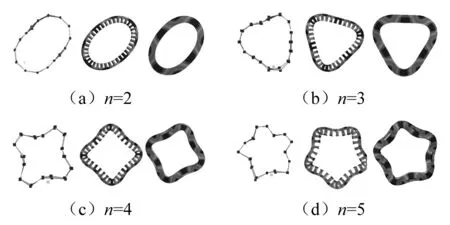
圖6 定子徑向模態振型Fig.6 Radial modal shapes of stator(m=0)

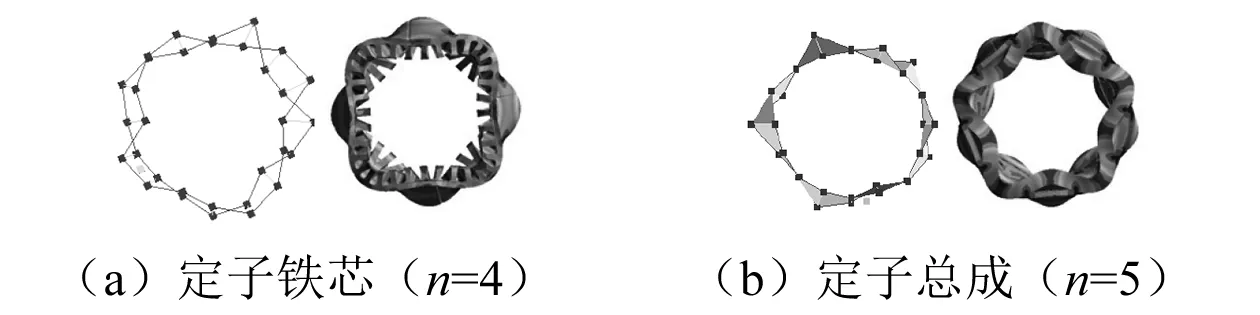
圖7 定子軸向模態振型(m=1)Fig.7 Axial modal shapes of stator(m=1)

3 爪極發電機自由模態有限元建模和試驗分析

3.1 爪極發電機自由模態有限元建模

發電機整機的有限元模型的精確性取決于零部件模型的準確建立和邊界條件的準確模擬。在第二節中已經獲取了定子鐵芯和繞組的各向異性材料參數，建立了每個部件準確的有限元模型，本節將重點考慮各零部件之間連接關系的模擬。爪極發電機的端蓋與定子之間并不是完全的過盈配合，前后端蓋通過螺栓對定子進行夾緊，這就導致實際定子與前后端蓋之間的連接關系比較復雜，同時轉子通過軸承支撐在端蓋上。因此本文在爪極發電機整機自由模態有限元建模過程中考慮的主要因素是前后端蓋螺釘預緊力的影響以及零部件之間的接觸設置。

(1) 螺栓預緊力。前后端蓋通過螺栓連接對定子進行夾緊，文獻[12]將定子與端蓋直接剛性節點耦合，忽略了螺栓預緊力對發電機模態的影響。為了驗證螺栓預緊力對發電機模態頻率的影響，在有限元軟件中對不同預緊力下發電機端蓋和定子裝配體的模態特性進行了計算，結果如圖8所示。

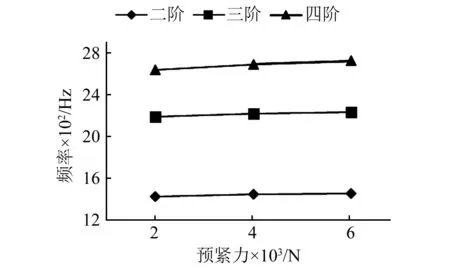
圖8 螺栓預緊力對模態頻率的影響Fig.8 Effects of bolt pretension on modal frequency

從圖8可知，當螺栓預緊力從2 000 N增加到6 000 N時，各階模態頻率都有所增加，特別是四階模態頻率增加了3%左右，說明螺栓預緊力會顯著影響裝配體的接觸剛度，對于發電機模態頻率特別是高頻模態的影響較大，因此在發電機整機的建模中需要考慮螺栓預緊力的影響。

(2)零部件接觸設置。定子與端蓋之間在冷態下屬于間隙配合，但是由于螺栓的夾緊作用，定子與端蓋之間存在著一定的接觸。因此在建模時為了模擬這種狀態，在四個螺栓夾緊位置設置了端蓋與定子的局部接觸。同時將轉子系統與軸承以MPC184單元連接，模擬兩者的相對轉動。

綜合考慮定子鐵芯和繞組的各向異性材料參數和各零部件之間的連接關系等影響因素，建立了爪極發電機自由模態有限元模型，如圖9所示。該模型共具有約60萬個單元。

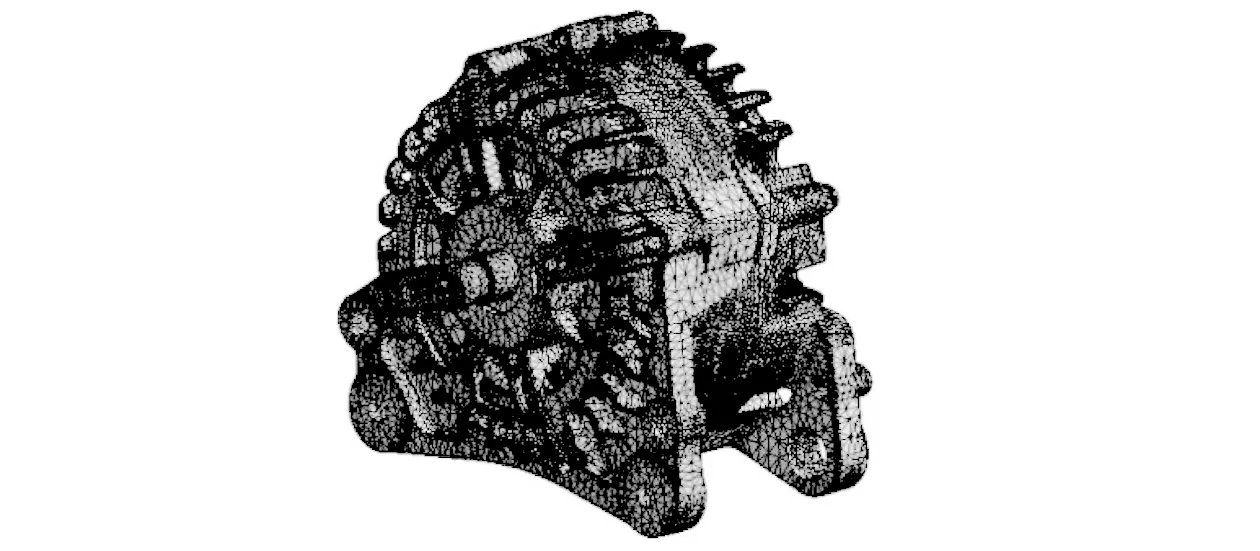
圖9 發電機整機有限元模型Fig.9 Finite element model of alternator

3.2 爪極發電機自由模態試驗分析

為了驗證上述發電機自由模態有限元模型的準確性，對該發電機的自由模態進行了試驗研究。同樣地，為了避免錘擊法的缺陷，采用和定子模態試驗相同的激振器法進行模態試驗。由于爪極發電機同時具有軸向和徑向模態，因此為了激發出發電機所有方向的模態，在進行整機的自由模態試驗時采用了兩個激振器在徑向和軸向進行激勵，如圖10所示。同時為了準確測定其振型，在發電機整機上布置了五圈測點，其中前后端蓋上各布置兩圈，在軸向中間位置布置了一圈測點，共47個測點，每個測點均采用三向傳感器來測量其軸向、徑向和切向振動。

圖10 發電機整機自由模態試驗Fig.10 Free modal test of alternator

根據試驗獲取了發電機整機在5 000 Hz以內的自由模態振型和模態頻率。試驗與有限元結果對比，如表4所示。

由表4可知，除了發電機整機的一階自由模態表現為轉子軸的前后移動，二階、三階、四階、五階的模態均表現為定子的變形，這也從側面解釋了中低頻下爪極發電機的振動與噪聲產生的原因：由于周期性變化的電磁力作用在電子齒面上，使定子發生變形，從而引起與之相連的端蓋振動,進而向外輻射噪聲。試驗結果和有限元模型結果的誤差在3%以內，符合工程實際要求，說明了本文在發電機自由模態模型建模過程中獲取的定子鐵芯和繞組各向異性材料參數以及對于邊界條件的模擬是準確的。

表4 發電機整機試驗與仿真結果對比Tab.4 Comparison of test results with simulation results of alternator

4 爪極發電機約束模態分析及振動測試

為了實現對爪極發電機整機振動與噪聲的數值預測，需要建立該發電機實際振動與噪聲測試條件下的約束模態有限元模型。實際振動與噪聲測試工況下發電機通過工裝夾具安裝在試驗臺上，拖動電機通過皮帶帶動發電機進行發電，如圖11所示。

在自由模態模型的基礎上，通過在工裝的四個地腳螺栓處施加固定約束，同時在皮帶輪處施加一豎直向下的拉力來考慮皮帶的預緊作用，建立了爪極發電機約束模態的有限元模型，如圖12所示。根據約束模態模型計算出的發電機模態振型和頻率，如圖13所示。各分圖的左圖為發電機振型的整體視圖，右圖為定子鐵芯局部視圖。

圖11 發電機整機安裝圖Fig.11 Installation of alternator

圖12 發電機約束模態有限元模型Fig.12 Constrained FE model of alternator

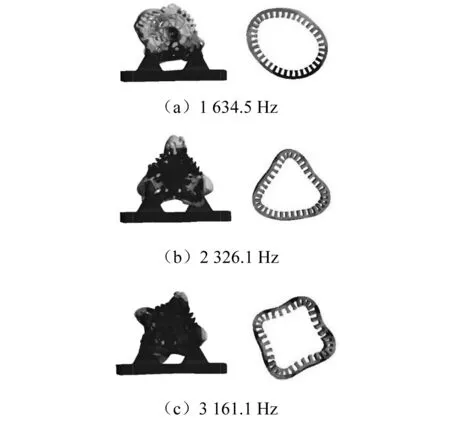
圖13 發電機整機約束模態振型Fig.13 Constraint modal shapes of alternator

由于發電機安裝在試驗臺上，激振器無法進行布置，而錘擊法又難以測量高頻模態，因此不易進行約束模態試驗。而實際工作過程中爪極發電機轉速范圍較寬，最高轉速可達10 000 r/min以上，因此電磁力頻率的分布范圍也相對較廣，易于發生結構共振。因此可以通過振動測試結果來間接驗證模態結果的準確性。

爪極發電機的振動主要是由機械因素、電磁因素和冷卻風扇引起的。當爪極發電機工作在中低轉速(6 000 r/min)以下時，電磁振動占主導地位，超過6 000 r/min時，扇葉表面壓力的周期性脈動以及渦的脫落、產生和破裂引起的振動占據主導地位[13]。本文主要研究電磁力引起的結構共振，因此關注發電機在6 000 r/min以下的振動。圖14為加速條件下爪極發電機端蓋上某點的徑向振動瀑布圖。

由圖14可知，該爪極發電機在1 600～1 700 Hz、2 200～2 400 Hz和3 100～3 300 Hz區間內發生明顯的共振現象，這與有限元模型計算的約束模態結果相一致，從而間接證明了本文所建立的約束模態模型的準確性。該模型可以進一步用于爪極發電機振動與噪聲的數值預測和減振降噪研究。

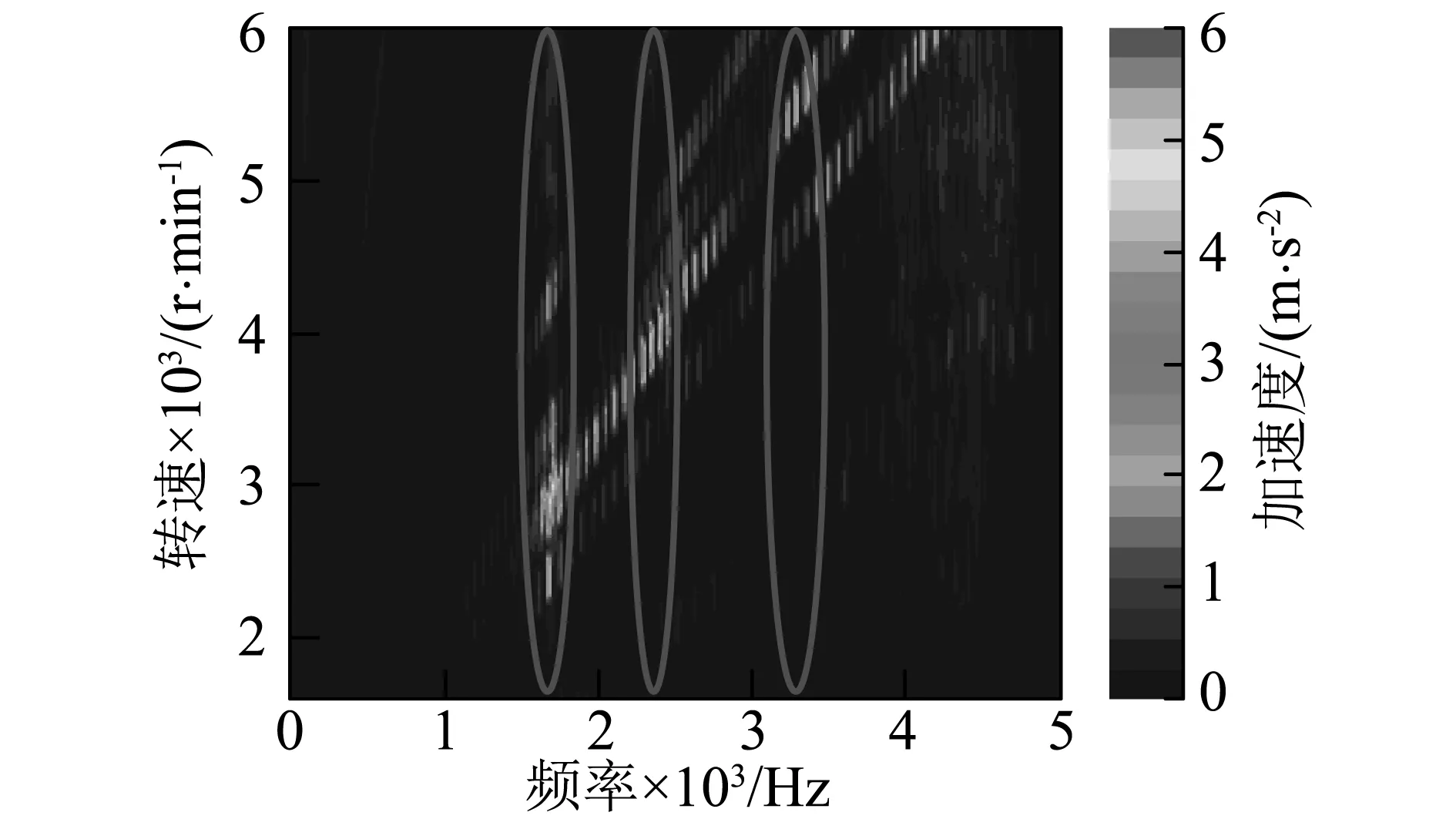
圖14 徑向振動加速度瀑布圖Fig.14 Waterfall plot of radial vibration acceleration

5 結 論

本文以車用爪極發電機為研究對象，提出了一種獲取定子鐵芯和繞組的各向異性材料參數的方法，根據獲取的參數建立了爪極發電機整機的自由模態和約束模態有限元模型。模態試驗和振動測試結果證實了所建立的整機有限元模型的有效性，為爪極發電機振動與噪聲的數值預測和減振降噪研究奠定了基礎。獲取的主要結論如下：

(1)由于層疊效應的影響，鐵芯和繞組軸向(z向)的材料特性明顯不同于徑向和切向(x和y方向)的材料特性，采用各向同性材料建模會帶來較大誤差。

(2)定子鐵芯和繞組的各向異性材料參數是準確預測定子系統固有頻率的關鍵，利用本文方法獲取的材料參數建立的定子系統的等效模型以及整機自由模態模型的仿真結果與試驗結果誤差均在3%以內。

(3)前后端蓋之間的螺栓預緊力會顯著影響裝配體的接觸剛度，使發電機模態頻率特別是高階模態的頻率顯著增加，在建模時應加以考慮。

[1]EVERSMANW,BURNSS,PEKAREKS,etal.Noisegenerationmechanismsinclawpolealternators[J].JournalofSound&Vibration, 2005, 283(1/2):369-400.

[2] LI J, WEI Q, YANG F, et al. Reduction of radial magnetic force waves based on eccentric magnetic pole for claw pole alternator[C]∥ Instrumentation and Measurement, Computer, Communication and Control (IMCCC), 2014 Fourth International Conference on. Harbin, China: IEEE, 2014:55-60.

[3] HATTORI T, NARITA K, YAMADA T, et al. Modeling method of vibration analysis model for permanent magnet motor using finite element analysis[C]// Electrical Machines and Systems, International Conference on. Tokyo, Japan: IEEE, 2009:1-6.

[4] 陳永校, 諸自強, 應善成．電機噪聲的分析與控制[M]. 杭州: 浙江大學出版社, 1987.

[5] 韓偉, 賈啟芬, 邱家俊. 異步電機定子的振動與模態分析[J]. 振動與沖擊, 2012, 31(17):91-94. HAN Wei, JIA Qifen, QIU Jiajun. Vibration and modal analysis for stator of an induction motor[J]. Journal of Vibration and Shock, 2012, 31(17):91-94.

[6] ISHIBASHI F, MATSUSHITA M, NODA S, et al. Change of mechanical natural frequencies of induction motor[J]. Industry Applications, IEEE Transactions on, 2010, 46(3):922-927.

[7] ISHIBASHI F, KAMIMOTO K, NODA S, et al. Natural frequency of stator core of small induction motor[J]. IEE Proceedings—Electric Power Applications, 2003, 150(2):210-214.

[8] 鮑曉華, 劉健, 倪有源,等. 汽車爪極發電機定子模態分析和固有頻率計算[J]. 汽車工程, 2011, 33(12):1088- 1091. BAO Xiaohua, LIU Jian, NI Youyuan,et al. Modal analysis and natural frequency calculation of the stator in automotive claw-pole alternator [J]. Automotive Engineering, 2011, 33(12):1088-1091.

[9] 謝穎, 王嚴, 呂森,等. 小型異步電機模態計算與試驗分析[J]. 電工技術學報, 2015, 30(16):1-9. XIE Ying, WANG Yan, Lü Sen,et al. Modal calculation and test of small asynchronous motor[J]. Translations of China Electrotechnical Society, 2015, 30(16):1-9.

[10] 代穎, 崔淑梅, 宋立偉. 車用電機的有限元模態分析[J]. 中國電機工程學報, 2011, 31(9):100-104. DAI Ying, CUI Shumei, SONG Liwei. Finite element method modal analysis of driving motor for electric vehicle[J]. Proceedings of the CSEE, 2011, 31(9):100-104.

[11] TANG Z, PILLAY P, OMEKANDA A M, et al. Young’s modulus for laminated machine structures with particular reference to switched reluctance motor vibrations[J]. Industry Applications IEEE Transactions on, 2004, 40(3):748 - 754.

[12] 尚修敏, 閆兵, 董大偉,等. 車用發電機的模態分析[J]. 噪聲與振動控制, 2014, 33(6):110-114. SHANG Xiumin, YAN Bing, DONG Dawei,et al. Modal Analysis of Vehicle Alternator[J]. Noise and Vibration Control, 2014, 33(6):110-114.

[13] 張亞東, 董大偉, 閆兵,等. 車用交流發電機氣動噪聲數值分析[J]. 振動與沖擊, 2015, 35(1): 174-182. ZHANG Yadong, DONG Dawei, YAN Bing,et al. Numerical simulation analysis for aerodynamic noise of a vehicle alternator[J]. Journal of Vibration and Shock, 2015, 35(1): 174-182.

Modal analysis of a claw-pole alternator considering orthotropy of the stator core and windings

DENG Wenzhe1, ZUO Shuguang1, SUN Han2, WU Shuanglong1, ZHANG Guohui1

(1. Clean Energy Automotive Engineering Centre, Tongji University, Shanghai 201804, China；2. Shanghai Valeo Automotive Electrical Systems Co. Ltd., Shanghai 201201, China)

Finite element (FE) and experimental modal analysis were conducted to analyze the inherent characteristics of a claw-pole alternator. Firstly, modal shapes and frequency were obtained through modal test for the stator, and orthotropic material parameters of the stator core and windings were then identified according to the finite element equivalent model and test results. Secondly, the FE model of free modal was built considering the complex connection between different components. The accuracy was validated through a free modal test. Finally, a constrained FE model was built on the basis of free modal and a vibration test was conducted. The results of the free modal test and the vibration test reveal that the modal characteristics can be precisely predicted through proposed model synthesizing orthotropic material parameters and bolt pretension. This work serves a foundation for prediction and reduction of vibration and noise.

claw-pole alternator; modal analysis; orthotropic; bolt pretension; vibration

國家自然科學基金資助項目(51375343)；重大科研儀器設備專項(2012YQ150256)

2016-01-05 修改稿收到日期： 2016-04-25

鄧文哲 男，博士生，1993年生

左曙光 男，博士，教授，博士生導師，1968年生

TM346

A

10.13465/j.cnki.jvs.2017.12.008