基于馬田系統的滾動軸承初始故障檢測和狀態監測

剡昌鋒, 朱 濤, 吳黎曉, 貝 克, 郭劍鋒

(1.蘭州理工大學 機電工程學院，蘭州 730050； 2.中核蘭鈾公司，蘭州 730060)

基于馬田系統的滾動軸承初始故障檢測和狀態監測

剡昌鋒1, 朱 濤1, 吳黎曉1, 貝 克1, 郭劍鋒2

(1.蘭州理工大學 機電工程學院，蘭州 730050； 2.中核蘭鈾公司，蘭州 730060)

針對軸承壽命的四個階段中振動信號特征參數的變化靈敏度不同，分析了特征參數對初始故障的敏感性和退化狀態的相關性，提出了一種采用馬田系統檢測軸承初始故障和區分性能退化狀態的方法。以對初始故障敏感和對退化狀態相關的特征參數建立了馬田系統的基準空間，并在馬田系統中將兩組特征參數融合為單一的特征參數馬氏距離； MD1對滾動軸承初始故障的敏感性，檢測軸承壽命在第一和第二階段時出現初始故障的時間點； MD2隨著滾動軸承性能退化狀態而不斷增大，依據其變化趨勢判斷軸承的退化狀態；該方法避免了單一特征參數在不同運行環境中的不確定性和不穩定性，可以準確的檢測出軸承的初始故障和判斷軸承的退化狀態。通過兩組滾動軸承加速壽命試驗，驗證了該方法的有效性和準確性。

馬田系統；滾動軸承；初始故障；狀態監測；相關性；

旋轉機械被廣泛應用于電力、石油、化工、冶金、機械、航空航天等重要工程領域，滾動軸承作為旋轉機械的關鍵部件，其性能退化或者失效將影響整機性能甚至導致設備非計劃停機，造成經濟損失甚至人員傷亡。據統計，約30%的旋轉機械故障是由于滾動軸承的損傷所造成的[1]。由于滾動軸承壽命分散性比較大，傳統的定時維修往往造成“維修不足”或者“維修過剩”，因此，滾動軸承初始故障的檢測和性能退化狀態的監測，對于保障設備長期安全、穩定運行和預知維修具有重要意義[2]。

近年來，許多學者在滾動軸承故障診斷方面做了大量的研究工作[3]，但是對軸承初始故障的識別和狀態監測分析方面還需要進一步的研究。軸承從出現故障到失效還有一段時間，如果采用初始故障檢測和狀態監測，盡早發現軸承故障，在失效前合理安排維修時間，就可以避免非計劃停機，減少維修成本，提高產品生產率。滾動軸承從出現故障到失效，建立一個合適的評價指標非常重要。由于單一的特征參數受抗干擾性差、敏感度低和包含信息少等缺點的制約，不能全面有效的評估軸承的性能退化狀態，因此，多參數評估滾動軸承的性能退化狀態得到了廣泛的應用。Zhao等[4]采用主成分分析進行多參數融合，應用互信息監測軸承的健康狀況。Shakya等[5]一方面應用馬田系統對軸承的健康狀況進行在線監測，通過切比雪夫不等式判斷軸承的狀態變化；另一方面應用正交化的馬田系統(Mahalanobis Taguchi Systen, MTS)識別滾動軸承故障類型并提出了缺陷發生指數[6]。Yu[7]通過動態主成分分析提取特征參數，采用基于馬氏距離(Mahalanobis Distance, MD)的隱馬爾卡夫模型對軸承的性能退化狀態進行在線監測。Wang等[8]應用基于EMD-SVD的馬田系統，對軸承故障和退化狀態進行監測。余發軍等[9]應用改進型的K-SVD字典學習算法和峭度最大化原則的稀疏分解算法提取滾動軸承早期故障特征參數。Lim等[10]分別應用滾動軸承振動信號低頻和高頻特征參數對軸承狀態的第二、第三階段進行跟蹤監測。Hu等[11]應用MTS-SOM系統對軸承初始故障和退化狀態進行跟蹤監測。Soylemezoglu等[12]應用馬田系統對滾動軸承進行故障檢測和壽命預測。Shen等[13]應用基于支持向量機的方法提取特征參數，該特征的發展趨勢與軸承的故障發展趨勢和運行時間相符合。Zhu等[14]采用基于SVDD的IRSVDD方法構建軸承的性能退化指標，克服了SVDD的缺點。Yan等[15]采用EMD和峭度相結合的方法，對軸承初始故障的時間進行估計。Kang等[16]通過二進制算法對軸承早期故障進行診斷和分類。Bhende等[17]采用聲發射技術對滾動軸承早期故障進行檢測和分類。目前多參數評估軸承退化狀態主要集中于多參數融合技術、各階段監測技術以及模型預測技術等方面。但是，多參數評估軸承退化狀態中存在兩個重要的問題：首先是要選擇合適的特征參數，該參數對軸承的退化狀態比較敏感并且其變化規律符合軸承的性能退化狀態；其次，需要選擇合適的方法，使得新的特征參數能夠正確反映軸承的性能退化狀態。

針對以上問題，本文提出了應用敏感性和相關性分析分別優化滾動軸承初始故障檢測和狀態監測時馬田系統的基準空間，選擇對初始故障敏感和退化狀態相關的特征參數構建馬田系統的基準空間，根據優化后馬氏距離的變化趨勢，判斷軸承的初始故障和退化狀態。馬氏距離MD1在軸承出現故障時其幅值快速增大，隨著故障的發展又回落到正常水平，根據其變化規律，檢測軸承的初始故障。馬氏距離MD2隨著故障的發展而不斷增大，當軸承狀態發生改變時，其變化更加明顯，根據其變化規律，判斷軸承的退化狀態。該方法確定的特征參數降低了馬田系統原始基準空間的維度，其特征參數的變化趨勢更加符合軸承初始故障和性能退化狀態的特點，根據馬氏距離的變化趨勢可以準確的判斷軸承的初始故障和退化狀態。

1 馬田系統基本原理

馬氏距離MD是由印度統計學家Mahalanobis P C于1936年提出的，表示數據的協方差距離[18]。與歐式距離相比，馬氏距離不受量綱的影響，兩點之間的馬氏距離與原始數據的測量單位無關；由標準化數據和中心化數據(即原始數據與均值之差)計算出兩點之間的馬氏距離。

馬田系統MTS是田口玄一博士提出的一種研究多維系統的方法，該方法將馬氏距離與田口方法進行了有效集成，被廣泛應用于疾病診斷、數據分類、模式識別以及樣本的診斷、預測分析[19]。

本文通過分析滾動軸承振動信號特征參數對初始故障的敏感性和退化狀態的相關性優化馬田系統的基準空間，根據優化后馬氏距離的變化趨勢檢測軸承的初始故障和退化狀況，主要包括以下步驟[20]：①基準空間的確定；②基準空間的有效性驗證；③基準空間的優化；④計算樣本空間的馬氏距離。

1.1 基準空間的確定

為了區分滾動軸承存在故障時馬氏距離的變化特征，在構建馬田系統基準空間時采用滾動軸承無故障時樣本的特征參數作為馬田系統的基準空間，根據馬氏距離的變化趨勢，判斷軸承的性能退化狀態。

步驟1 構建基準空間特征參數

假定有m個特征參數，n個樣本，則第i次采集數據的第j個特征參數可以表示為Xij，第i個樣本的特征參數可以表示為Xi=(Xi1,Xi2, …,Xij,Xim)，則n個正常樣本特征參數的基準空間可以表示為：

(1)

步驟2 基準空間標準化

(2)

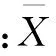
步驟3 計算標準化后基準空間的馬氏距離

(3)

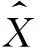
1.2 基準空間的有效性驗證

為了驗證基準空間的有效性，采集滾動軸承無故障階段和故障階段時的振動信號樣本，利用基準空間的均值、方差、相關矩陣對兩組樣本的基準空間進行標準化并計算其馬氏距離。如果故障樣本的馬氏距離明顯大于正常樣本的馬氏距離，則證明所建立的基準空間是有效的；否則，需要重新選擇特征參數定義基準空間。

1.3 基準空間優化

滾動軸承初始故障檢測和狀態監測過程中并非所有的特征參數都有助于提高計算精度，有些特征參數甚至存在干擾，因此，為了簡化馬氏距離的計算、縮短計算時間、提高診斷精度，需要對原始馬田系統的基準空間進行特征優化，選擇有效的特征參數構建馬田系統的基準空間。在滾動軸承初始故障檢測過程中，選擇對初始故障比較敏感的特征參數構建馬田系統基準空間；狀態監測過程中選擇與軸承退化狀態相關的特征參數構建馬田系統的基準空間。優化后的特征參數其變化趨勢更加符合軸承初始故障和退化狀態的特點，基準空間特征參數數目更少，計算更加簡單、高效，結果更加可靠。

1.4 樣本空間的馬氏距離

(4)

(5)

2 滾動軸承初始故障和狀態監測特征參數選擇

2.1 特征參數

滾動軸承初始故障檢測和狀態監測能否成功，在很大程度上取決于特征參數的選擇。滾動軸承振動信號分析中，常用的特征參數有時域特征、頻域特征和時頻特征。本文所選用的特征有時域特征：平均值、均方根、峰值、偏度、峭度、波峰因子、裕度因子、形狀系數、脈沖系數；頻域特征有：軸承內圈、外圈、滾動體、保持架的特征頻率幅值。各個特征計算方法如下[21]：

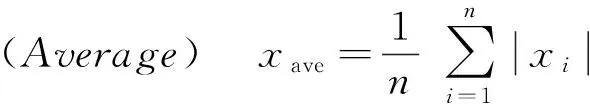
(6)

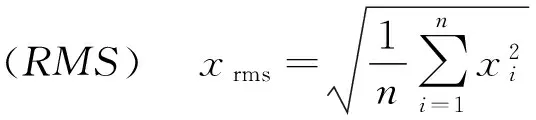
(7)

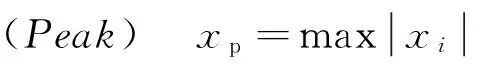
(8)

(9)

5)峭度(Kurtosis)

(10)

(11)

7)裕度因子(Clearance factor)

(12)

(13)

(14)

10)外圈特征頻率幅值：xbpfo

11)內圈特征頻率幅值：xbpfi

12)滾動體特征頻率幅值：xbsf

13)保持架特征頻率幅值：xftf

式中：xm為樣本數據的均值，xstd為樣本數據的標準差。xm計算公式如下：

(15)

滾動軸承特征頻率根據軸承幾何參數中的滾子數目z、滾動體直徑d、節圓直徑D、接觸角α以及軸承轉速n可以計算得到軸承的特征頻率[22]。滾動軸承特征頻率的幅值根據樣本時域信號的快速傅里葉變換計算得到。

2.2 滾動軸承初始故障特征參數選擇

2.2.1 初始故障特征參數敏感性分析

滾動軸承特征參數在初始故障時的敏感性主要指在初始故障期間特征參數達到峰值時的時間和幅值，也就是其特征參數達到峰值時的上升率，時間越短、幅值越大，其敏感性越高。為了準確描述各個特征參數在初始故障時的敏感性，采用滾動軸承第二階段時特征參數的峰值yp和時間xp的比值作為衡量敏感性s大小的標準。為了比較每個樣本特征參數敏感性的大小，消除幅值y在不同特征之間幅值差異的影響，計算敏感性s在不改變特征參數變化趨勢的情況下，對每個特征參數進行歸一化處理。

步驟1 特征參數歸一化

假定有n個樣本，則該樣本的某一個特征參數可以表示為X=(x1,x2, …,xi, …,xn)，其歸一化如下：

(16)

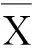
步驟2 敏感性計算

(17)

根據式(16)和式(17)可以對滾動軸承每一個特征參數進行歸一化和敏感性計算。特征參數的歸一化處理，避免了計算敏感性時不同特征參數幅值差異的影響，使每個特征參數的敏感性具有可比性。

2.2.2 初始故障特征參數選擇

滾動軸承的初始故障能否準確檢測，與初始故障特征參數選擇有很大的關系。滾動軸承初始故障檢測中選擇對初始故障敏感性較高的特征參數作為馬田系統的基準空間，根據馬氏距離的變化趨勢檢測軸承的初始故障。

為了分析滾動軸承初始故障時的敏感性，本論文所用實驗數據來源于IEEE PHM 2012，試驗采用的PRONOSTIA

平臺，如圖1所示[23]。數據采集中，采樣頻率為25.6 kHz，每次采集數據的時間間隔為10 s，采樣時間為0.1 s，每個樣本包含2 560個數據點。實驗的第1組數據共有1 416個樣本，其樣本的13個特征參數變化趨勢，如圖2～圖14所示。該實驗采集了滾動軸承加速壽命實驗中軸承從完好到自然失效時全壽命周期的數據。

圖1 PRONOSTIA試驗平臺Fig.1 Test rig of PRONOSTIA

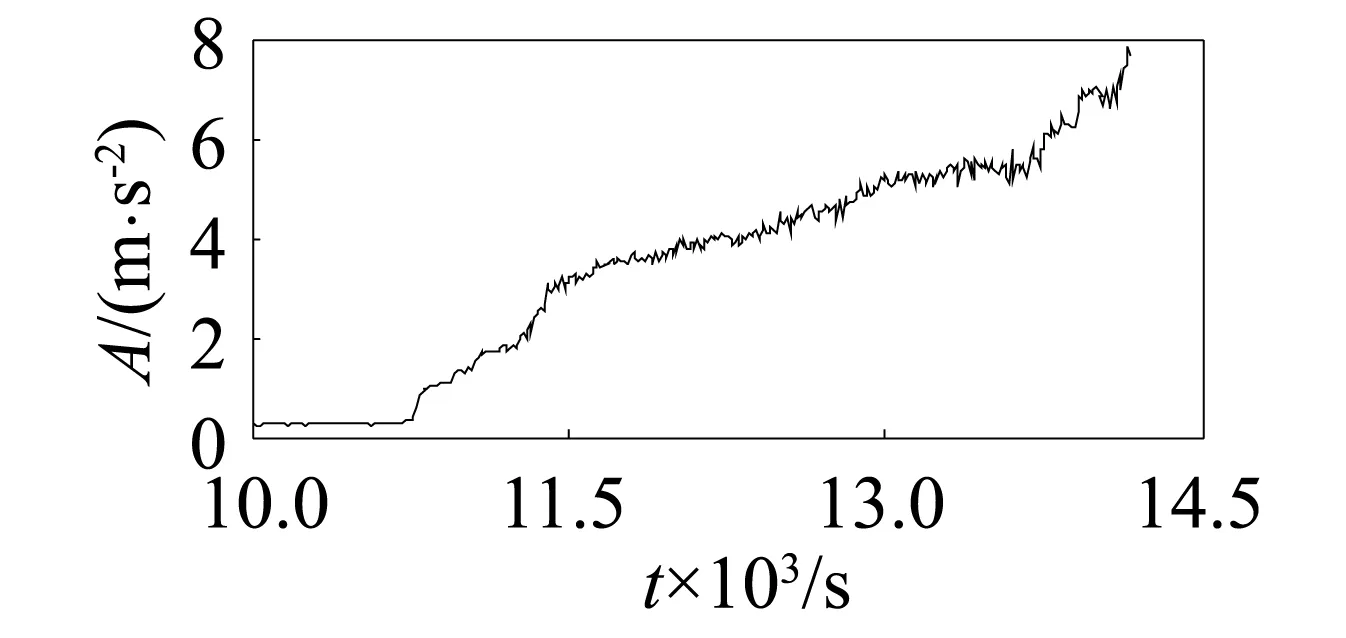
圖2 平均值Fig.2 Average

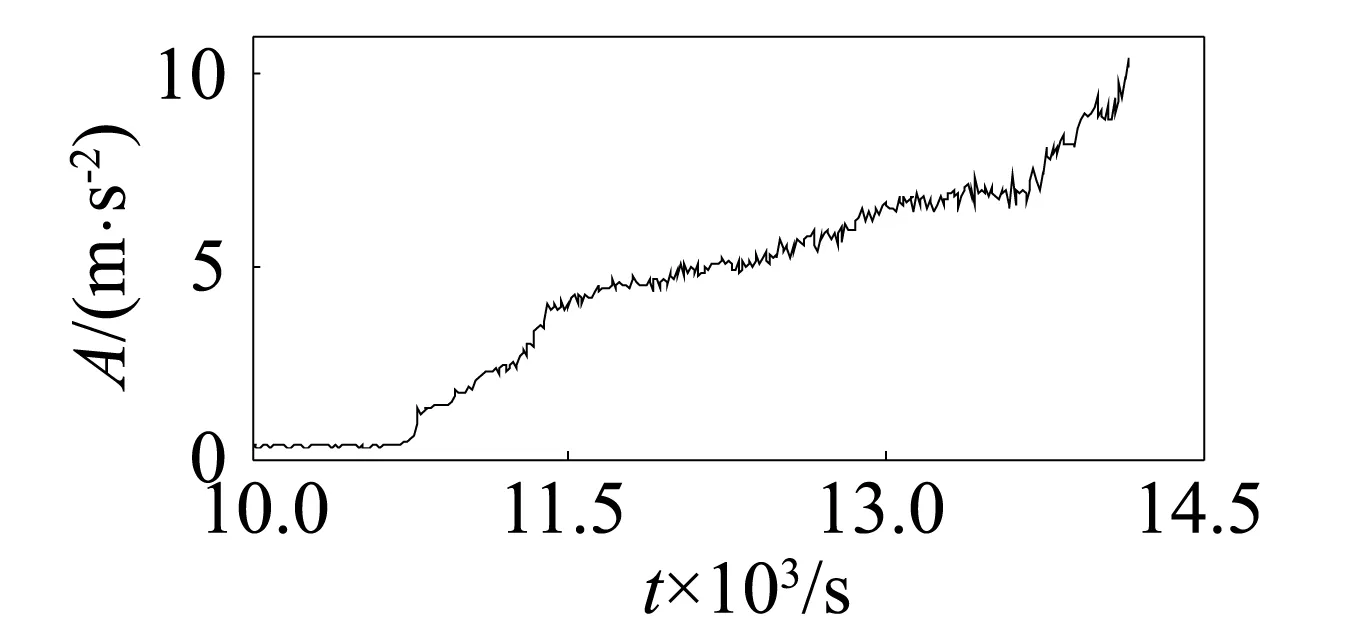
圖3 均方根Fig.3 RMS

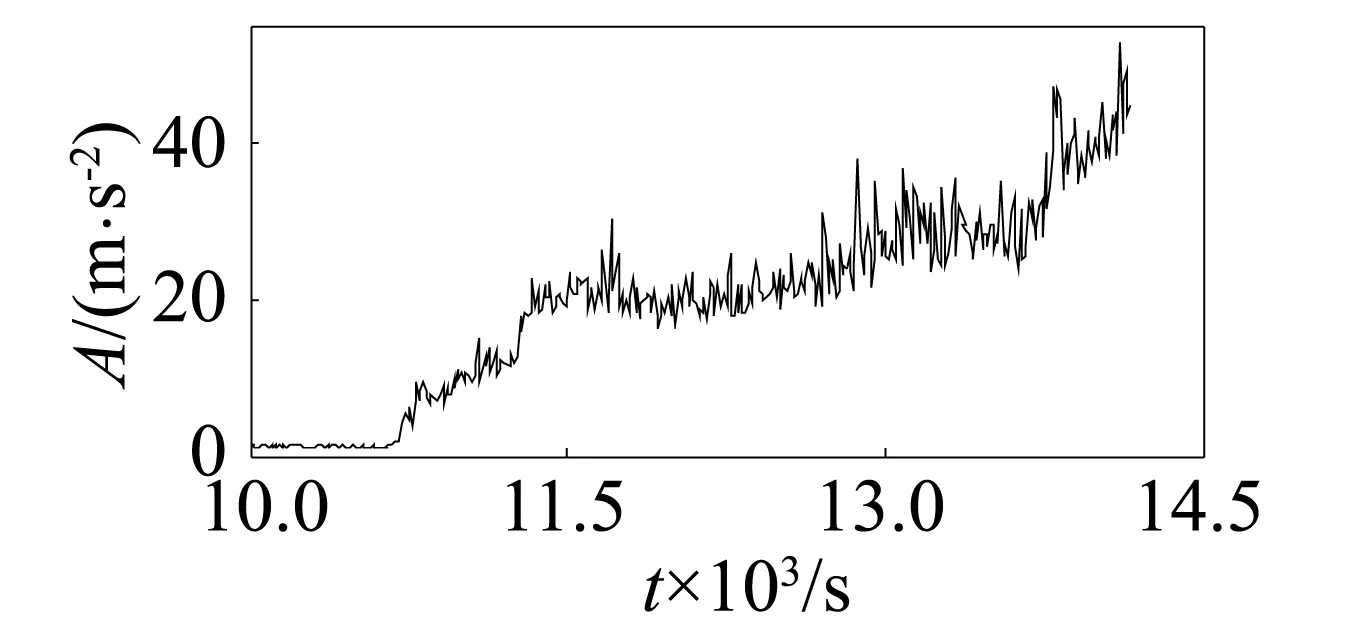
圖4 峰值Fig.4 Peak

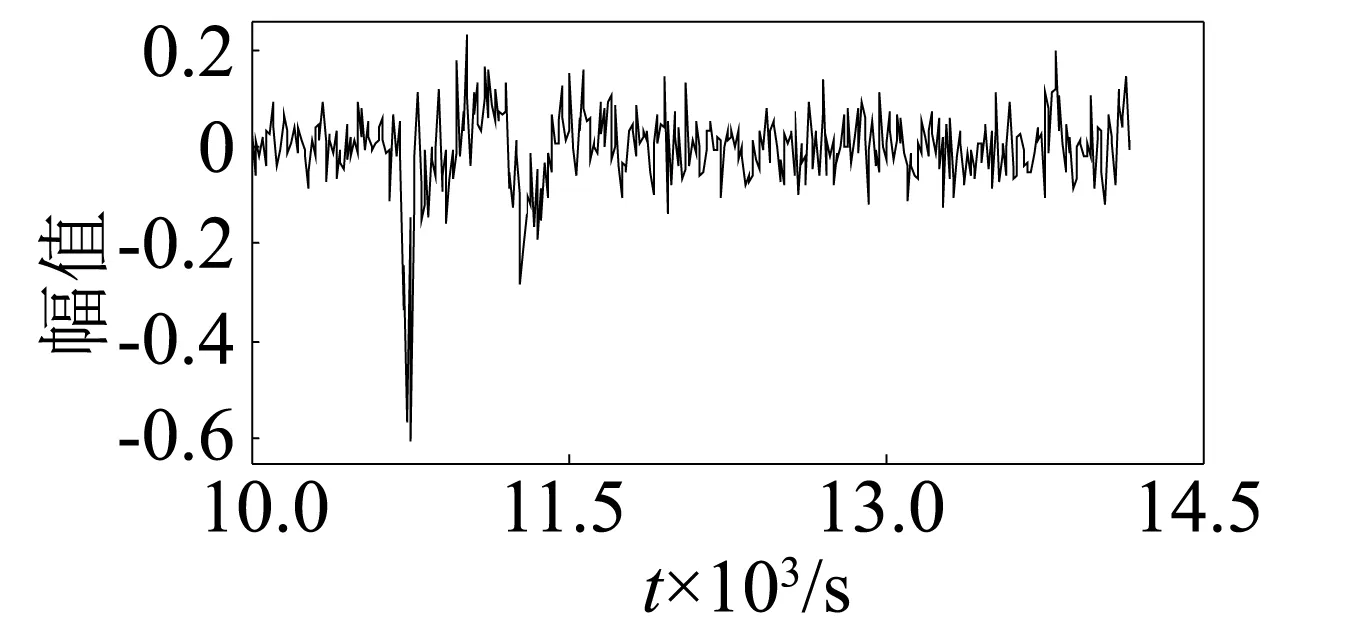
圖5 偏度Fig.5 Skewness

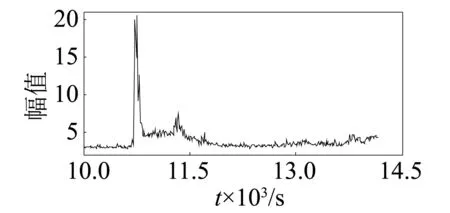
圖6 峭度Fig.6 Kurtosis

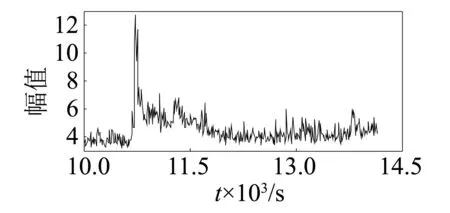
圖7 波峰因子Fig.7 Crest factor

圖8 裕度因子Fig.8 Clearance factor

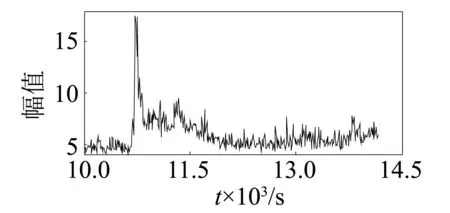
圖10 脈沖系數Fig.10 Impulse factor

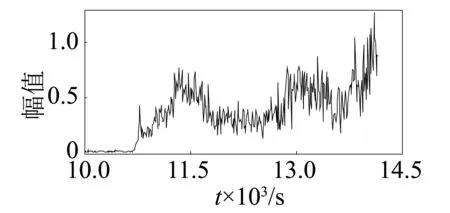
圖11 外圈特征頻率Fig.11 Feature frequency of outer race

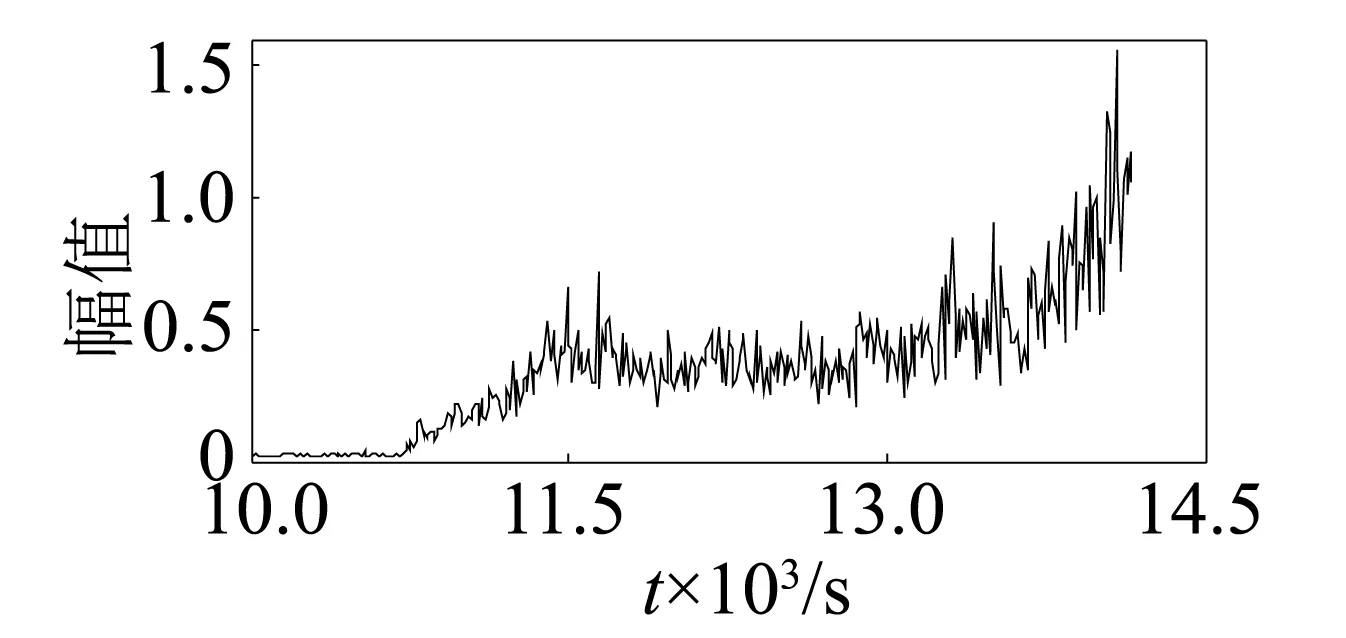
圖12 內圈特征頻率Fig.12 Feature frequency of inner race

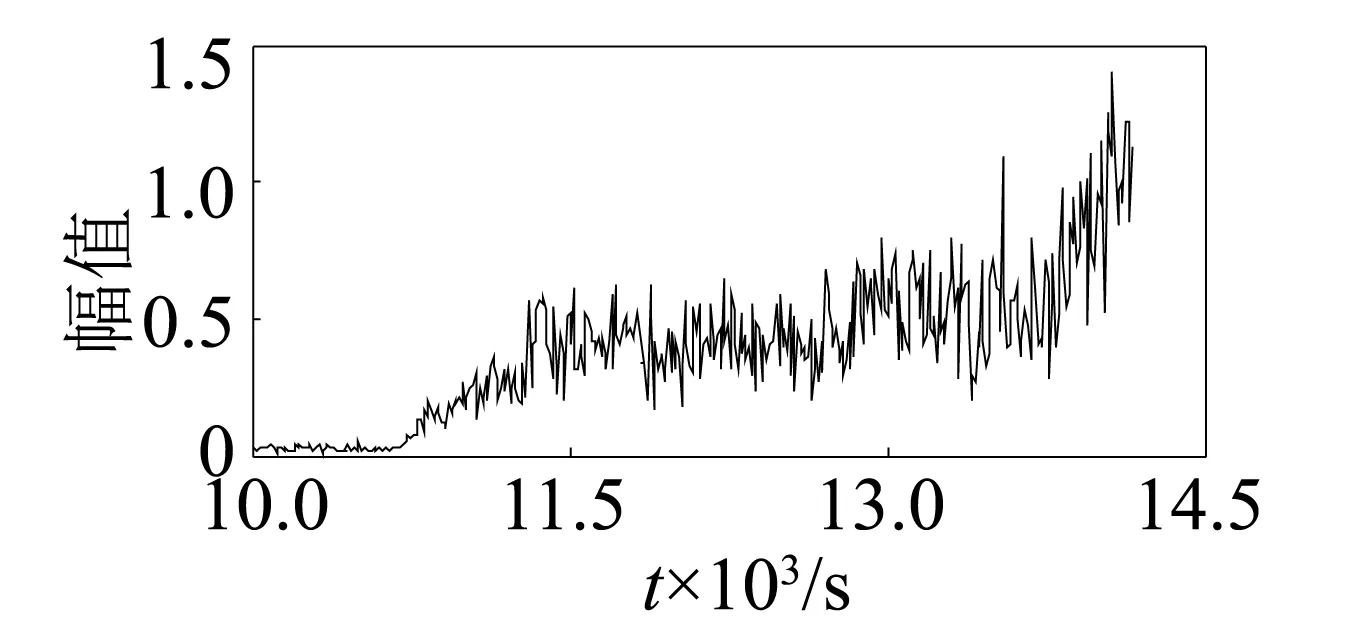
圖13 滾動體特征頻率Fig.13 Feature frequency of ball

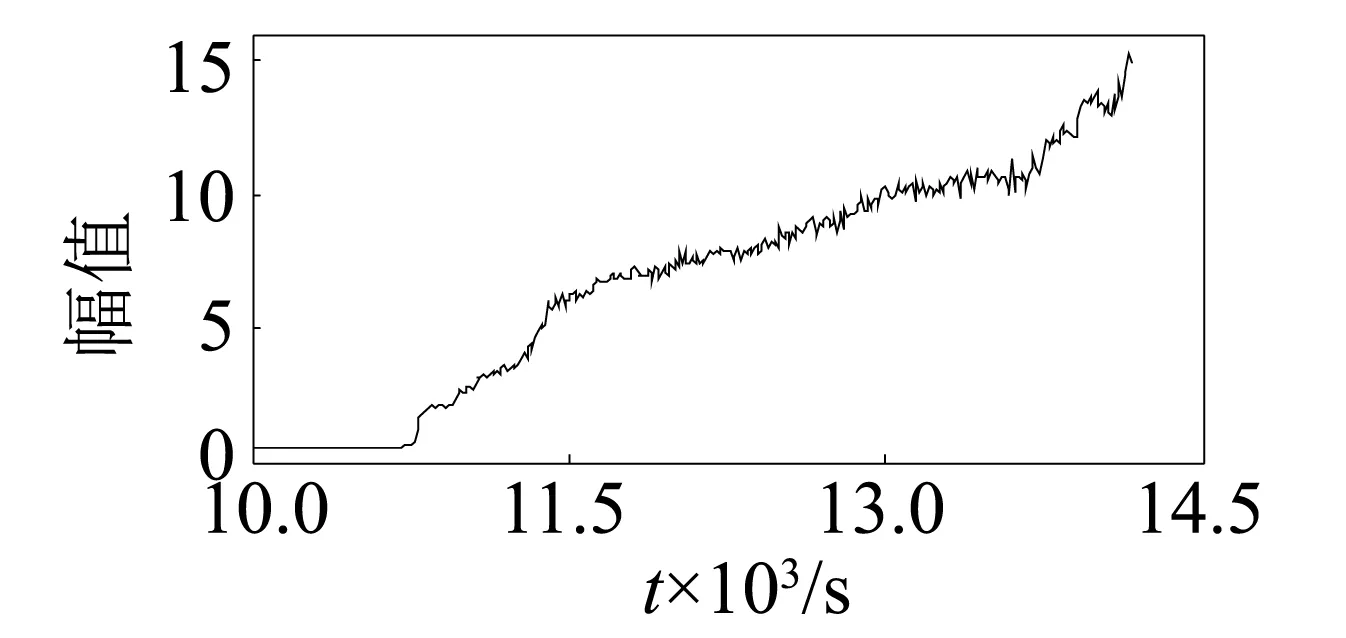
圖14 保持架特征頻率Fig.14 Feature frequency of cage

應用式(16)和式(17)對以上13個特征參數以及IEEE PHM 2012中的其它3組實驗數據進行早期故障敏感性分析，如表1所示。

通過第1組實驗數據的敏感性可知，13個特征參數敏感性由高到低依次為：峭度、波峰因子、裕度因子、脈沖系數、形狀系數、偏度、峰值、外圈特征頻率、滾動體特征頻率、保持架特征頻率、平均值、均方根。根據第1組實驗數據的敏感性及其變化趨勢可以看出，敏感性較高的峭度、波峰因子、裕度因子、脈沖系數、形狀系數前5個特征參數(圖6～圖10)在軸承出現初始故障時其幅值快速增大，變化非常明顯，其它特征參數在初始故障期間變化比較平穩。

通過表1可知，其它3組實驗中峭度、波峰因子、裕度因子、脈沖系數、形狀系數5個特征參數的敏感性排列在前5名，其敏感性高且穩定性好。在滾動軸承初始故障檢測過程中，如果增加特征參數，其馬氏距離可能在初始故障時變化不明顯；減少特征參數數目，其馬氏距離可能在初始故障時幅值減小。因此，在滾動軸承初始故障預測過程中，使用峭度、波峰因子、裕度因子、形狀系數、脈沖系數5個特征參數構建馬田系統的基準空間，用于檢測滾動軸承的初始故障是合理的。

表1 特征參數早期故障的敏感性Tab.1 Sensitivity of features in incipient fault

2.3 滾動軸承退化狀態特征參數選擇

2.3.1 相關性分析

相關性分析可以判斷兩個特征之間的相互聯系或相互依賴關系。根據特征參數與軸承退化狀態的相關性，選擇與軸承退化狀態相關性較大的特征參數作為檢測軸承退化狀態的特征參數構建馬田系統的基準空間。相關性分析選擇的特征參數更加符合軸承的退化狀態，避免了其它特征參數的影響，對于準確判斷軸承的退化狀態有重要意義。

兩個長度相同的向量A=(A1,A2,…,Am)和B=(B1,B2,…,Bm)之間的相關性可以通過如下公式計算：

(18)

2.3.2 特征參數選擇

滾動軸承從開始到失效經歷了四個階段：滾動軸承無故障階段、滾動軸承輕微故障階段、滾動軸承嚴重故障階段和滾動軸承失效階段。滾動軸承退化狀態評估中，構造一個合適的特征參數最為重要，該參數應該隨著故障的發展而不斷增大且變化規律符合軸承的退化狀態，才能更好的利用其變化規律監測軸承的運行狀態。

滾動軸承狀態監測特征參數選擇過程中，根據13個特征參數為基準空間的馬氏距離MD(圖15)和13個特征參數的變化趨勢(圖2～圖14)可以看出，MD的變化趨勢更加符合軸承的退化狀態，其變化趨勢與軸承的性能退化狀態有很好的相關性。滾動軸承狀態監測特征參數優化過程中，將馬氏距離MD作為軸承退化狀態的基準，分析13個特征參數與馬氏距離MD的相關性，選擇相關性較大的特征參數作為馬田系統的基準空間，根據優化后馬氏距離的變化趨勢，判斷軸承的退化狀態。

為了驗證特征參數在不同實驗中特征參數與退化狀態的相關性，使用IEEEPHM2012中6組試驗數據，分析13個特征參數與其馬氏距離的相關性，其結果如表2所示。

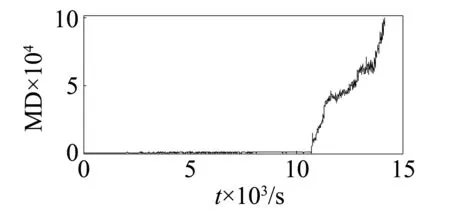
圖15 馬氏距離MDFig.15 Mahalanobis distance MD

通過表2可知：平均值、均方根、峰值和滾動軸承4個特征頻率幅值的7個特征參數與其馬氏距離的相關性高且穩定性好。經過相關性分析降低了馬田系統基準空間的維度，分析得出的7個特征參數比原始13個特征參數數量更少，其特征參數的變化趨勢更加符合軸承的退化狀態。因此，在滾動軸承狀態監測過程中，使用平均值、均方根、峰值和滾動軸承4個特征頻率幅值的7個特征參數構建馬田系統的基準空間，用于檢測滾動軸承初始故障是合理的。

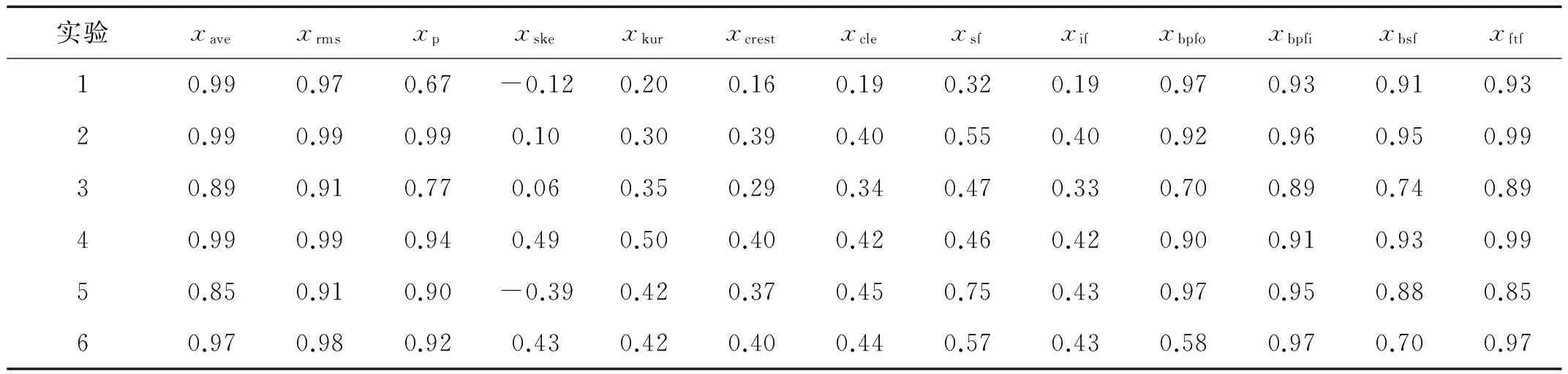
表2 特征參數與馬氏距離的相關性Tab.2 Correlation of feature and MDs

3 實驗驗證和討論

3.1 案例1

3.1.1 滾動軸承初始故障檢測

為了驗證峭度、波峰因子、裕度因子、形狀系數、脈沖系數5個特征參數作為馬田系統基準空間時檢測初始故障的準確性。分別采用實驗中全部13個特征參數和峭度、波峰因子、裕度因子、形狀系數、脈沖系數5個特征參數作為馬田系統的基準空間，其兩組特征參數的馬氏距離MD和MD1的變化趨勢，如圖16所示。

圖16 兩種馬氏距離的比較Fig.16 Comparison of two MDs

通過圖16中馬氏距離MD和MD1變化趨勢可知，馬氏距離MD1在1 072處幅值明顯增大，達到2 784，高于前期最大值940.1，并且在1 079處達到最大值6 236，在1 084處減小到1 074。根據馬氏距離的變化趨勢可以判斷，軸承在該時段出現了早期故障，其馬氏距離在故障初始階段達到了最大值，其變化趨勢比馬氏距離MD的變化趨勢更加明顯，用于檢測軸承的初始故障更加有效。因此，用敏感性分析確定的特征參數比原始特征參數數目更少，降低了馬田系統基準空間的維度，優化后特征參數的馬氏距離其識別初始故障的能力更強。

3.1.2 滾動軸承狀態監測

為了進一步驗證平均值、均方根、峰值和滾動軸承內圈特征頻率、外圈特征頻率、滾動體特征頻率、保持架特征頻率7個特征參數作為馬田系統基準空間時監測軸承狀態的準確性，分別采用實驗中全部13個特征參數和相關性優化后的7個特征參數作為馬田系統的基準空間，其兩組特征參數的馬氏距離MD和MD2的變化趨勢，如圖17所示。為了進一步觀察馬氏距離在狀態改變時的變化趨勢，將軸承第二階段到第三階段時的變化趨勢局部放大，如圖17所示。滾動軸承狀態改變時，其各點幅值及狀態改變量，如表3所示。

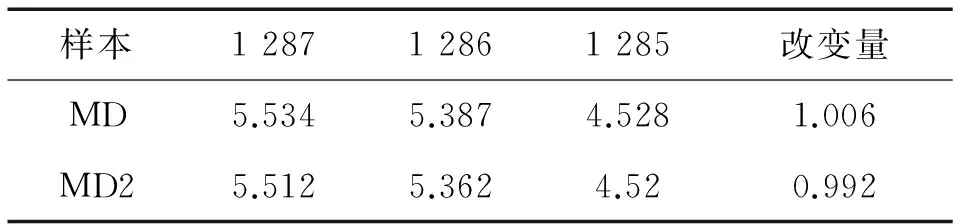
表3 第3階段的狀態改變量Tab.3 Condition changes of stage 3

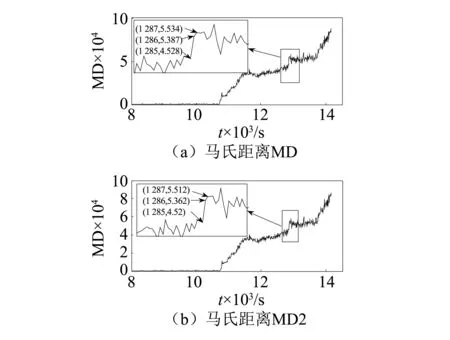
圖17 馬氏距離MD和MD2的比較Fig.17 Comparison of MD and MD2

通過圖17可知，馬氏距離MD和MD2的變化趨勢比較接近，并且其相關性為99.9%。在狀態改變時，用1287樣本的幅值和1285樣本幅值的差值定義為狀態改變量，在狀態改變時MD的改變量為1.006，MD1的改變量為0.992，MD的改變量比MD2的改變量多0.014，占MD改變量的1.4%。

根據相關性分析優化的特征參數和狀態改變量可以看出，優化后的7個特征參數比原始13個特征參數減少了6個，特征空間維度降低了46%，而優化后馬氏距離的狀態改變量與原始馬氏距離的改變量只差1.4%，并且其馬氏距離變化趨勢非常相似，優化后的特征參數構建的馬田系統完全可以代替原始特征參數構建的馬田系統。

通過應用相關性分析優化后的7個特征參數構建馬田系統基準空間，其馬氏距離MD2的變化趨勢能準確的判斷軸承的退化狀態，其壽命的四個階段比較明顯，其各個階段變化趨勢，如圖18所示。

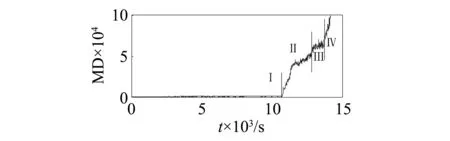
圖18 馬氏距離MD2Fig.18 Mahalanobis distance MD2

根據MD2的變化趨勢和軸承四個階段的特點，滾動軸承的四個階段分別為：第1階段1～1 071；第2階段1 072～1 374；第3階段：1 375～1 285；第4階段：1 286～1 416。

3.2 案例2

為了驗證該方法在其它軸承以及其它環境中的有效性，本文采用了Intelligent Maintenance Systems提供的數據IMS Bearing Data，該實驗所使用試驗平臺，如圖19所示[24]。試驗用的測試軸承為Rexnord ZA-2115 雙列球軸承。試驗中，數據采樣頻率為20 kHz，軸承轉速為2 000 r/min，每次采樣間隔為10 min，采樣時間為1 s，每個樣本含有20 480個數據點，試驗樣本為1 991個。

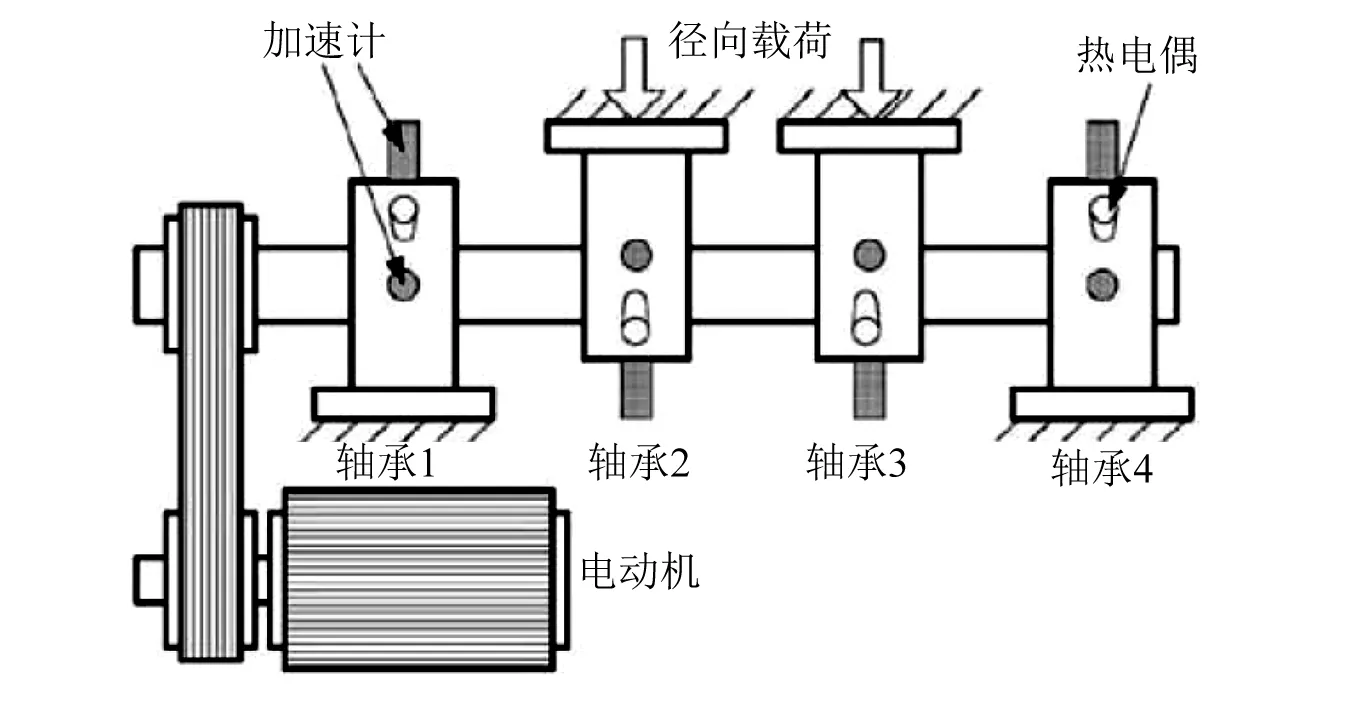
圖19 軸承測試臺Fig.19 Bearing test rig

根據滾動軸承初始故障檢測和狀態監測時的特征參數，分別應用IMS Bearing Data，將滾動軸承初始故障敏感性較高的峭度、波峰因子、裕度因子、形狀系數、脈沖系數5個特征參數和滾動軸承退化狀態相關的平均值、均方根、峰值和滾動軸承4個特征頻率幅值的7個特征參數分別作為馬田系統的基準空間進行滾動軸承初始故障檢測和狀態監測，結果如圖20所示。從圖20(a)可知，由峭度、波峰因子、裕度因子、形狀系數、脈沖系數構成馬田系統基準空間的馬氏距離MD1在1667個樣本中出現了早期故障，其變化趨勢在初始故障階段比較明顯，可以檢測軸承的初始故障。從圖20(b)可知，由平均值、均方根、峰值和滾動軸承4個特征頻率幅值的7個特征參數構成馬田系統基準空間的馬氏距離中，可以明顯的看出滾動軸承壽命發展的四個階段，各階段變化比較明顯，適合用于監測軸承的退化狀態。

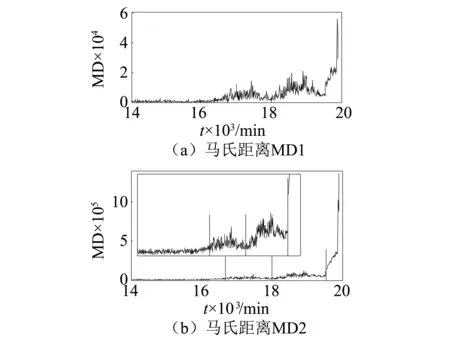
圖20 兩種馬氏距離的性能退化比較 Fig. 20 Performance degradation comparison of two MDs

綜上所述，本文提出的基于馬田系統的初始故障檢測和狀態監測的方法可以準確有效的判斷出軸承的初始故障和退化狀態。運用敏感性分析和相關性分析優化馬田系統基準空間的特征參數，優化后的特征參數其變化趨勢更加符合軸承的初始故障和退化狀態的特點，根據馬氏距離的變化趨勢可以準確判斷出軸承的初始故障和軸承壽命的四個階段。

馬田系統在滾動軸承狀態監測過程中，由于故障具有復雜性和多變性，部分軸承故障畸形發展和演化，其特征參數變化不規則，狀態監測過程中馬田系統還有一定的不足，需要進一步的研究，克服這些缺點。

4 結 論

基于馬田系統的滾動軸承早期故障檢測和狀態監測中，通過特征參數早期故障敏感性分析和退化狀態的相關性分析，得出了軸承早期故障敏感的特征參數和退化狀態相關的特征參數，去除了其它特征參數的影響。運用馬田系統將兩組特征參數融合為單一的特征參數：馬氏距離，根據馬氏距離的變化趨勢，判斷軸承的初始故障和退化狀態。通過兩個實驗，驗證了該方法在早期故障檢測和狀態監測中的有效性和準確性。

[1] LEE J, WU F J, ZHAO W Y, et al. Prognostics and health management design for rotary machinery systems—Reviews, methodology and applications [J]. Mechanical Systems and Signal Processing, 2014, 42(1/2): 314-334.

[2] 佟佩聲. 滾動軸承變工況條件下靜電監測特征提取及故障程度識別方法研究[D]. 南京：南京航空航天大學，2014.

[3] PATIL M S. MATHEW J, RAJENDRAKUMAR P K. Bearing signature analysis as a medium for fault detection a review[J]. Journal of Tribology, 2007，130(1)： 14001-14007.

[4] ZHAO X M, ZUO M J, PATEL T. EMD, ranking mutual information and PCA based condition monitoring [C]∥ Proceedings of the ASME 2010 International Design Engineering Technical Conferences & Computers and Information in Engineering Conference. Montreal, Canada, 2010 .

[5] SHAKYA P, MAKARAND S K, DARPE A K. A novel methodology for online detection of bearing health status for naturally progressing defect [J]. Journal of Sound and Vibration, 2014, 333(21): 5614-5629.

[6] SHAKYA P, MAKARAND S K, DARPE A K. Bearing diagnosis based on Mahalanobis-Taguchi-Gram-Schmidt method[J]. Journal of Sound and Vibration, 2015, 337: 342-362.

[7] YU Jianbo. Health condition monitoring of machines based on hidden markov model and contribution analysis [J]. IEEE Transactions on Instrumentation and Measurement, 2012, 61(8): 2200-2211.

[8] WANG Zhipeng, LU Chen, WANG Zili, et al. Fault diagnosis and health assessment for bearings using the Mahalanobis-Taguchi system based on EMD-SVD [J]. Transactions of the Institute of Measurement and Control, 2013, 35(6): 798-807.

[9] 余發軍，周鳳星，嚴保康. 基于字典學習的軸承早期故障稀疏特征提取[J]. 振動與沖擊，2016，35(6):181-186. YU Fajun, ZHOU Fengxing, YAN Baokang. Bearing initial feature extraction via sparse representation based on dictionary learning[J]. Journal of Vibration and Shock, 2016, 35(6):181-186.

[10] LIM R, KEONG C, MBA D. Bearing time-to-failure estimation using spectral analysis features [J]. Structural Health Monitoring, 2014, 13(2): 219-230.

[11] HU Jinqiu, ZHANG Laibin, LIANG Wei. Dynamic degradation observer for bearing fault by MTS-SOM system[J]. Mechanical Systems and Signal Processing, 2013, 36 (2): 385-400.

[12] SOYLEMEZOGLU，JAGANNATHAN S，SAYGIN C. Mahalnobis Taguchi System (MTS) as a prognostic tool for rolling element bearing failures[J]. Journal of Manufacturing Science & Engineering, 2010, 132(5):635-645.

[13] SHEN Zhongjie, HE Zhengjia, CHEN Xuefeng, et al. A monotonic degradation assessment index of rolling bearings using fuzzy support vector data description and running time [J]. Sensors, 2012, 12(8): 10109-10135.

[14] ZHU Xiaoran, ZHANG Youyun, ZHU Yongsheng. Bearing performance degradation assessment based on the rough support vector data description [J]. Mechanical Systems and Signal Processing, 2013, 34 (1/2): 203-217.

[15] YAN Changfeng, YOU Li, KONG Yuanyuan, et al. A hybrid method to estimate initial faulty time of rolling bearing [J]. International Conference on Control System and Automation, 2013, 8(9): 474-480.

[16] KANG M, KIM J, KIM J M. Reliable fault diagnosis for incipient low-speed bearings using fault feature analysis based on a binary bat algorithm [J]. Information Sciences, 2015, 294: 423-438.

[17] BHENDE A R, AWARI G K, UNTAWALE S P. Comprehensive bearing condition monitoring algorithm for incipient fault detection using acoustic emission [J]. Jurnal Tribologi, 2014(2): 1-30.

[18] WANG Zhipeng, WANG Zili, TAO Laifa, et al. Fault diagnosis for bearing based on Mahalanobis-Taguchi System [C]∥ 2012 Prognostics and System Health Management Conference. Denver, USA, 2012.

[19] ELHAM A. Mahalanobis Taguchi system: a review [J]. Emerald Insight, 2015, 32(3): 291-307.

[20] 任江濤，蔡遠文，史建偉，等. 基于馬田系統的設備健康監測技術研究[J]. 計算機測量與控制，2012，20(3): 634-641. REN Jiangtao, CAI Yuanwen, SHI Jianwei, et al. Research on equipment health monitoring using Mahalanobis-Taguchi system [J]. Computer Measurement and Control, 2012, 20(3): 634-641.

[21] 何正嘉，陳進，王太勇，等. 機械故障診斷理論及其應用[M]. 北京：高等教育出版社，2010.

[22] BRIAN P G, KEN S. Rolling element bearing analysis[J]. Materials Evaluation, 2011, 70(1): 78-85.

[23] NECTOUX P, GOURIVEAU R, MEDJAHER K, et al. PRONOSTIA: An experimental platform for bearings accelerated life test [C]∥ IEEE International Conference on Prognostics and Health Management. Denver, USA, 2012.

[24] LEE J, QIU H, YU G, et al. Rexnord technical services: bearing data set [EB/OL].http:∥ti.arc.nasa.gov/tech/dash/pcoe/prognostic-data-repository/, 2007.

Incipient fault detection and condition monitoring of rolling bearings by using the Mahalanobis-Taguchi System

YAN Changfeng1, ZHU Tao1, WU Lixiao1, AHMED Y Y1, GUO Jianfeng2

(1.School of Mechanical and Electrical Engineering, Lanzhou University of Technology, Lanzhou 730050, China;2. Lanzhou Uranium Enrichment Company of China Nuclear Industry Corporation，Lanzhou 730060，China)

Because the sensitivity of feature parameters of vibration signal are different with the four-stage of bearing life, the sensitivity to incipient fault and the correlation of degradation condition were analyzed in this work. A new method of incipient fault detection and performance degradation was presented by the Mahalanobis-Taguchi System (MTS). The feature parameters which were sensitive to incipient fault and related performance degradation condition were treated as a reference space for the Mahalanobis-Taguchi System (MTS). Two groups of feature parameters were fused with single feature parameters in MTS of Mahalanobis distance. Since MD1 is more sensitive to incipient fault of bearings, it was used to detect the time of incipient fault during the first and second stages of bearing life. According to MD2 increasing with performance degradation, the degradation state of bearings was estimated by variation tendency. By using this method, the uncertainty and instability of single feature parameters could be avoided in different running condition. The incipient fault was also detected accurately and degradation condition of bearings life was distinguished. The validity and accuracy of this method were verified by the service life of rolling bearing in an accelerated life test.

Mahalanobis-Taguchi System (MTS); rolling bearing; incipient fault; condition monitoring; correlation

國家自然科學基金項目(51165018)

2015-12-14 修改稿收到日期： 2016-05-09

剡昌鋒 男，博士，研究員，1974年生

TH133

A

10.13465/j.cnki.jvs.2017.12.026