基于等效次級的直線感應(yīng)電機的電磁分析與參數(shù)辨識

邸 珺 范 瑜 劉亞靜

(北京交通大學(xué)電氣工程學(xué)院 北京 100044)

?

基于等效次級的直線感應(yīng)電機的電磁分析與參數(shù)辨識

邸 珺 范 瑜 劉亞靜

(北京交通大學(xué)電氣工程學(xué)院 北京 100044)

提出一種基于等效次級的直線感應(yīng)電機空載試驗的方法：采用軟磁鐵氧體材料模擬次級背鐵，達到電機次級電流為零、但勵磁電感保持不變的空載試驗要求。建立電磁場二維模型，解析計算次級材料相對磁導(dǎo)率對勵磁電感的影響；在勵磁電感不變的前提下，根據(jù)次級背板相對磁導(dǎo)率和勵磁電感的解析式，設(shè)計等效次級的幾何參數(shù)，通過有限元計算與試驗測量進行驗證。該文在數(shù)學(xué)上對勵磁電感的表達式做了適當(dāng)化簡，使其能夠適用于直線感應(yīng)電機的控制。

直線感應(yīng)電機 參數(shù)辨識 空載試驗 勵磁電感

0 引言

近年來直線感應(yīng)電機(Linear Induction Motor，LIM)的應(yīng)用越來越廣泛，對直線感應(yīng)電機的理論探究也愈發(fā)深入和精細(xì)。其中，越來越多的研究將建立一個精準(zhǔn)且便于控制的直線感應(yīng)電機等效電路作為其目標(biāo)，對直線感應(yīng)電機的電磁參數(shù)進行進一步地分析與探討[1，2]。與此同時，參數(shù)辨識在各類電機的研究中也愈發(fā)重要[3-8]。

空載試驗的目的是測量電機的勵磁參數(shù)。在T型等效電路中，如圖1所示，傳統(tǒng)空載試驗測量電機勵磁電感時，要求電機次級電流為零(理想空載試驗)或近似為零(滑差率接近0)。但由于直線感應(yīng)電機氣隙較大，運行速度難以接近同步速度，無論離線參數(shù)辨識還是在線參數(shù)辨識，要進行傳統(tǒng)空載試驗，就需要通過輔助裝置將電機拖動到同步速度[9，10]。對于磁懸浮列車或輪軌交通車輛的直線牽引電機，由于其安裝在轉(zhuǎn)向架上，還帶有變頻器和控制設(shè)備，既無法實現(xiàn)理想的空載運行，也難以用其他車輛將其拖動到同步速度。即使是機床等所用的直線電機，盡管可能得到接近空載的條件，由于其往復(fù)運動的特點，實際上處于不斷的暫態(tài)過程中，也難以用傳統(tǒng)方法獲得其穩(wěn)態(tài)等效電路參數(shù)。

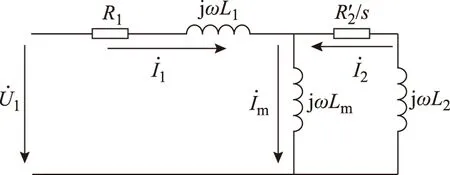
圖1 直線感應(yīng)電機T型等效電路Fig.1 T-type equivalent circuit of LIM

由于傳統(tǒng)空載試驗不易進行，替代傳統(tǒng)空載試驗的參數(shù)辨識方法成為直線感應(yīng)電機理論研究中的熱點問題之一，并有文獻對此問題進行了相應(yīng)探討：文獻[11] 提出了基于PWM變頻器輸出量的離線計算方法，通過最小二乘法間接計算獲得電機初級和次級電阻、初級和次級漏感等參數(shù)；文獻[12]提出的擴充域模型參數(shù)辨識方法同樣采用了最小二乘法進行數(shù)據(jù)處理，通過電機輸入輸出數(shù)據(jù)反代得到電機參數(shù)；文獻[13]提出了基于Park變換的雙邊直線感應(yīng)電機參數(shù)計算方法，顯然雙邊直線感應(yīng)電機不需要考慮次級背鐵的作用；文獻[14]建立了dq坐標(biāo)系下的電機模型，通過有限元計算對直線感應(yīng)電機的等效電路進行了研究；文獻[15-17]采用繞組分析的方法，考慮直線感應(yīng)電機的端部效應(yīng)，進行了參數(shù)計算。

上述文獻中的參數(shù)計算方法主要基于電機的繞組分析，將電機的電磁場簡化為電路。由電機學(xué)理論可知，電路的分析方法適用于氣隙較小、磁場分布均勻的旋轉(zhuǎn)電機，而直線感應(yīng)電機氣隙較大，氣隙磁場沿法向分布不均勻，需要對直線感應(yīng)電機的電磁場進行分析。文獻[18，19]研究了非磁性次級感應(yīng)電機的磁場和特性。文獻[20]詳細(xì)地給出了經(jīng)典的單邊直線感應(yīng)電機電磁場分析。文獻[21]通過一維電磁場建模導(dǎo)出了直線感應(yīng)電機等效電路。文獻[22，23]認(rèn)為次級背板的相對磁導(dǎo)率無窮大且厚度可忽略，這樣就忽略了次級背板對氣隙磁場和勵磁電感的影響。文獻[22-24]主要通過仿真軟件計算并對比不同次級下的電機特性，未給出次級參數(shù)對電機性能影響的完整解析方法。

本文從電磁場出發(fā)，提出了一種基于等效次級的直線感應(yīng)電機參數(shù)測量方法：用導(dǎo)磁性好但電導(dǎo)率低的軟磁鐵氧體模擬直線電機的背鐵，建立直線感應(yīng)電機電磁場的二維模型，解析計算空載試驗時次級材料對氣隙磁場的影響，并得到次級材料與勵磁電感的解析表達式；基于由次級背板相對磁導(dǎo)率表示的勵磁電感的表達式，在保持勵磁電感不變的前提下，根據(jù)替代前后的相對磁導(dǎo)率，折算等效次級的幾何尺寸，進行等效次級參數(shù)測量試驗。試驗結(jié)果表明，該方法簡單有效，有助于對電機電磁場的深入理解與運用，并適用于電機控制系統(tǒng)的設(shè)計。

1 LIM電磁場模型

1.1 電磁場數(shù)學(xué)模型

直線感應(yīng)電機的隨體坐標(biāo)系如圖2所示。本文認(rèn)為電機次級固定，初級沿x軸正向平動，以初級幾何中線為y軸，原點在次級導(dǎo)電板上表面，建立二維電磁場模型。根據(jù)相對磁導(dǎo)率，將直線感應(yīng)電機分成F1、F2、F3區(qū)域，分別表示氣隙和次級導(dǎo)電板、次級背板、外界空氣。

圖2 直線感應(yīng)電機隨體坐標(biāo)系Fig.2 The boby-fixed coordinate system of LIM

對于Fi(i=1，2，3)區(qū)域，標(biāo)其上、下邊界(即對應(yīng)的y軸坐標(biāo))分別為yi-1和yi，則氣隙高度為y0，次級導(dǎo)電板(鋁板)厚度為-y1，次級背板厚度d2a=y1-y2(a=1，2；d21表示背鐵，d22表示鐵氧體背板)；特別地，F(xiàn)3區(qū)域下界為無窮遠點。根據(jù)直線感應(yīng)電機的結(jié)構(gòu)特點，首先做出以下假設(shè)以便化簡：

1)認(rèn)為磁場僅存在于初級對應(yīng)區(qū)域，設(shè)初級長度[-X，X]，初級寬度[-Z，Z]。

2)忽略初級齒槽，用行波電流層替代初級磁動勢，并只考慮基波分量。定義β=π/τ(τ為極距，單位為m)，認(rèn)為三相對稱，行波電流層表示為

ks=ezReKsej(βx-ωt)

3)各層物理參數(shù)均勻，是各向同性的。

由于頻率較低，可認(rèn)為行波電流層形成準(zhǔn)靜態(tài)電場，則麥克斯韋方程組中的位移電流可以忽略。根據(jù)麥克斯韋方程組，對于無電流區(qū)域，有

(1)

其通解表達式為

Hi=exHix+eyHiy

(2)

其中

(3)

式中，參數(shù)Pi、Qi為待定復(fù)數(shù)，需在邊界yi-1和yi上取合適的邊界條件進行求解。

1.2 端部效應(yīng)的修正

由于直線感應(yīng)電機的鐵心開斷，在分析其電磁場時需對電機的端部效應(yīng)進行考慮，特別是第二類縱向端部效應(yīng)。第二類縱向端部效應(yīng)由直線感應(yīng)電機的運動和磁場開斷引起，是直線感應(yīng)電機的本質(zhì)特征，因此，通過數(shù)學(xué)方法對電機運動方向上的電磁場進行解析即可得出其表達式。這里，對理想空載條件下的直線感應(yīng)電機進行一維電磁場分析，從而獲得端部效應(yīng)對電磁場的影響。

理想空載條件下，次級的運行速度與同步速度相等，因此，在電機中取貫穿氣隙-次級的窄小矩形，根據(jù)麥克斯韋方程組，有

(4)

式中，kr為次級的感應(yīng)渦流。邊界條件為

H|x=±X=0

不妨設(shè)磁場強度的通解表達式為

H=eyReHe-jωt將其代入式(4)，并結(jié)合行波電流層的表達式，解二階常微分方程可得H在初級長度[-X，X]范圍內(nèi)的分布為

(5)

式中，參數(shù)A1、A2為復(fù)數(shù)，可表示為

(6)

將式(6)表達的端部效應(yīng)表達式代入式(3)中進行修正，可得理想空載條件下計及端部效應(yīng)的磁場強度表達式為

(7)

1.3 分層區(qū)域傳遞矩陣

空載試驗時，次級不存在感應(yīng)電流，因此除F1區(qū)域的上邊界y0，其余待求區(qū)域均為無電流區(qū)，滿足式(1)。邊界y1、y2是介質(zhì)的分界面，根據(jù)分界面銜接條件有

(8)

不妨設(shè)Fi區(qū)域的參數(shù)矩陣為

(9)

(10)

設(shè)Fi區(qū)域的相對磁導(dǎo)率為μir，則μ1r=μ3r=1。整理式(7)～式(10)，解得相鄰兩區(qū)域傳遞矩陣為

(11)

相應(yīng)地，有

(12)

(13)

顯然，傳遞矩陣為反對稱矩陣。

1.4 邊界條件及求解

在F1區(qū)域的上邊界y0處，依據(jù)全電流定律，有第一類邊界條件，解得

P1sinh (βy0)+Q1cosh(βy0)=Ks

在F3區(qū)域的下邊界處，磁力線為零，滿足第一類邊界條件，即

解得

P3=Q3

由式(10)、式(11)、式(13)，從F3區(qū)域依次向上迭代，解得在F1區(qū)域，參數(shù)P1、Q1分別為

(14)

另經(jīng)反向迭代，可由傳遞矩陣求解F2、F3區(qū)域參數(shù)，為

將式(14)代入式(7)，并考慮到背板材料，無論是鐵還是軟磁鐵氧體，相對磁導(dǎo)率μ2r>>1，則y方向參數(shù)可化簡為

(15)

由上述分析可以看出，在主磁場中，磁場強度在x方向和y方向耦合，并且與背板的相對磁導(dǎo)率和厚度均有關(guān)。若要主磁場的磁場強度嚴(yán)格處處保持不變，則需改變y2使得式(15)中兩個表達式的值恒定，但實質(zhì)上自變量維數(shù)低于待求量維數(shù)，大部分情況下無解。另外待求解的方程組為超越方程組，即使有解析解，但形式復(fù)雜不便應(yīng)用于工程中，因此需要通過其他方式保證勵磁電感不變。

1.5 磁場儲能及電感參數(shù)

在Fi區(qū)域中，磁場儲存的能量可表示為

(16)

根據(jù)空載試驗方法，不難得知，在初級與輸入電壓不變的前提下，要使得勵磁參數(shù)不變，需要保證采用等效次級時電機主磁路的磁場儲能與傳統(tǒng)直線感應(yīng)電機主磁路的磁場儲能相等。

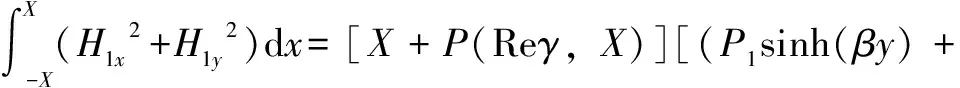
Q1cosh (βy))2+(P1cosh(βy)+

[(P1sinh(βy)+Q1cosh (βy))2-

(P1cosh(βy)+Q1sinh(βy))2]

(17)

式中，函數(shù)P(Reγ，X)表示對端部效應(yīng)諧波中x分量的積分。式(17)中，前一部分不含時間t，為穩(wěn)態(tài)分量，后一部分與時間t有關(guān)，為暫態(tài)分量。然而根據(jù)β的定義，sin(2βX)=0，暫態(tài)分量為零。因此，在本文的電磁場分析模型中，勵磁參數(shù)與時間無關(guān)。定義背板的表征函數(shù)f(μ2r，y2)，表示背板材料與幾何參數(shù)對勵磁電感的影響，由上述分析，勵磁電感可表示為

Lm=2μ0Z[X+P(Reγ,X)]f(μ2r,y2)

(18)

其中，表征函數(shù)f(μ2r，y2)的表達式如式(19)所示。在勵磁電感一定時，要求背板的表征函數(shù)恒定。

f(μ2r,y2)=

(19)

考慮電機的幾何尺寸，由于β(y1-y2)→0，對式(19) 進行二階泰勒展開，并代入到式(18)，可得

Lm= 2μ0Z[X+P(Reγ,X)]·

(20)

記背鐵相對磁導(dǎo)率為μ21，下邊界y軸坐標(biāo)為y21；等效背板的相對磁導(dǎo)率為μ22，下邊界y軸坐標(biāo)為y22。替換前、后次級相對磁導(dǎo)率發(fā)生變化時，要保證電機勵磁電感不變，根據(jù)式(20)，解得y22如式(21)所示。

(21)

式(20)、式(21)表明，雖然直線感應(yīng)電機的勵磁電感受端部效應(yīng)的影響，但等效背板的厚度與端部效應(yīng)無關(guān)。式(21)給出了在次級背板的相對磁導(dǎo)率發(fā)生變化時保持電機勵磁電感不變的等效次級厚度。在等效次級的求解過程中，即使氣隙中主磁場的磁場分布不一定與原分布處處相等，但等效前、后主磁場的磁場儲能維持不變，意味著直線感應(yīng)電機在等效前、后勵磁電感保持不變，表明通過等效次級可以測量直線感應(yīng)電機空載參數(shù)。

2 有限元計算

2.1 計算對象和參數(shù)設(shè)置

本文采用有限元計算，以常見的短初級單邊直線感應(yīng)電機(Single-sided Linear Induction Motor，SLIM)為例，對直線感應(yīng)電機電磁場的理論分析與解析計算表達式進行驗證。這里本文保持替換前、后兩種背板的幾何尺寸不變，而改變材料的相對磁導(dǎo)率和電導(dǎo)率(替換前、后材料分別為背鐵、軟磁鐵氧體)。

有限元計算的兩個對象分別為采用傳統(tǒng)次級和采用等效次級的SLIM，因為仿真過程需考慮電機的運動，故選擇瞬態(tài)磁場對二者分別求解。在幾何結(jié)構(gòu)上，二者參數(shù)設(shè)置相同：氣隙5 mm，次級導(dǎo)電板2 mm，次級背板1 mm，各區(qū)域邊界的y軸坐標(biāo)依次為y0=0，y1=-7 mm，y2=-8 mm。此外，電機初級條件相同：采用矩形槽，繞組匝數(shù)100匝，單層整距繞組，激勵為三相對稱工頻電流源。但二者的次級材料有所差別，其對比見表1，其中σ、μr分別為材料電導(dǎo)率和相對磁導(dǎo)率。

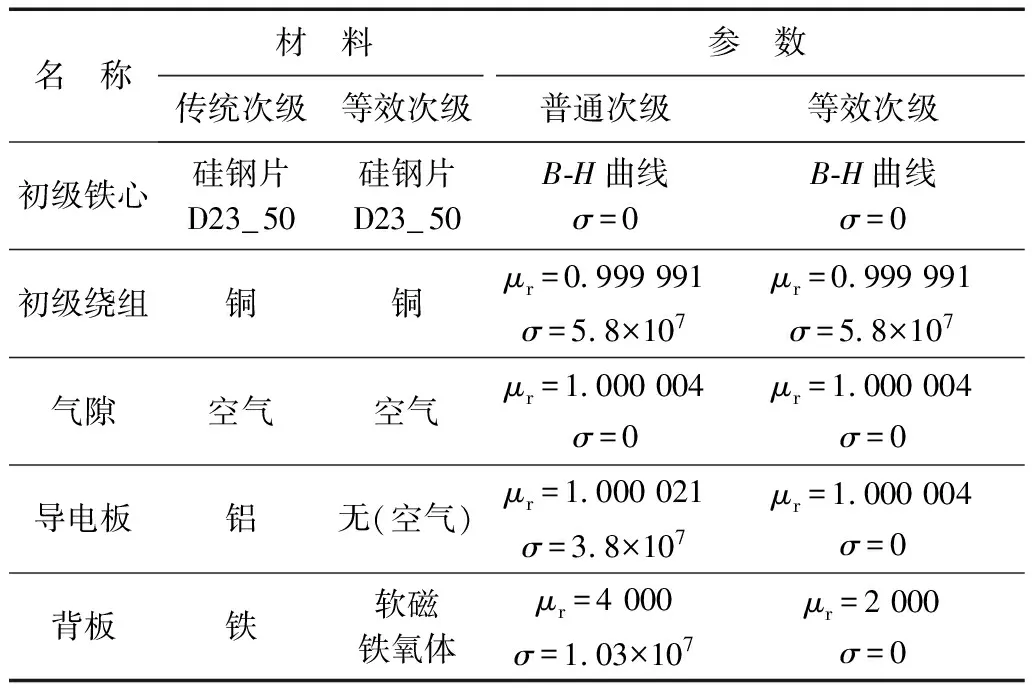
表1 有限元計算SLIM材料參數(shù)

可以看到，除了電機次級(次級導(dǎo)電板、次級背板)材料的參數(shù)，電機的其他參數(shù)均相同。通過仿真對材料相對磁導(dǎo)率與磁場強度分布的表達式進行驗證。

2.2 計算結(jié)果

對傳統(tǒng)次級SLIM進行空載試驗，即：SLIM運行至同步速7.15 m/s；對于等效次級SLIM，由于次級不導(dǎo)電，初級和次級間無相對運動，運動設(shè)置中的速度為0。要注意的是，在軟件計算中，空載試驗容易實現(xiàn)，而在實際測量中，特別是在城市軌道交通車輛領(lǐng)域，由于直線感應(yīng)電機初級安裝在車體上，難以達到真正的空載狀態(tài)。除此之外，直線感應(yīng)電機位置重復(fù)性差、輔助拖動設(shè)備消耗較大，導(dǎo)致實際的空載試驗幾乎不可能進行。

圖3為氣隙中的磁場強度H的場量云圖，可以看出，二者的磁場強度H分布規(guī)律大致相同，但具體數(shù)值有所區(qū)別。

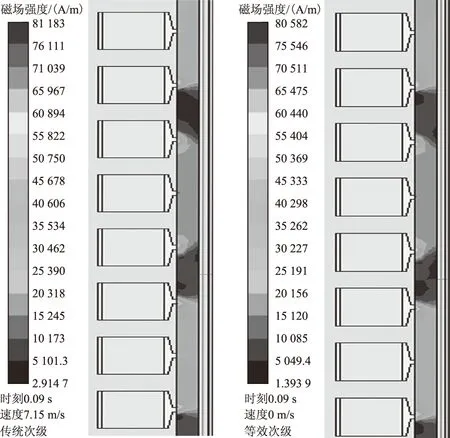
圖3 SLIM傳統(tǒng)空載試驗和等效次級空載試驗中的氣隙磁場強度云圖Fig.3 The field figure of SLIM in traditional no-load test and the one with the equivalent secondary

不失一般性，選擇氣隙中y=-2.5 mm處平行于x軸的一條直線，計算沿這條直線的切向磁場強度Hx和法向磁場強度Hy。替換前、后的磁場強度分量對比曲線如圖4、圖5所示。圖中，Hx和Hy均呈周期性變化，容易看出其變化周期為2τ，這與理論公式中x方向參數(shù)相符。需要注意的是，仿真中初級齒槽的影響在理論分析的前提中不予考慮，因此圖4、圖5中出現(xiàn)了理論中未出現(xiàn)的奇次諧波(顯然曲線未發(fā)生相移，因此認(rèn)為不含有偶次諧波)。

圖4 氣隙中Hx沿x軸分布Fig.4 The distribution of Hx in air gap along x-axis

圖5 氣隙中Hy沿x軸分布Fig.5 The distribution of Hy in air gap along x-axis

圖6中，對Hx和Hy分別進行快速傅里葉變換(Fast Fourier Transformation，F(xiàn)FT)，可以看出，切向分量和法向分量的基波分別為3.235 Hz、3.052 Hz，理論計算出x方向參數(shù)的頻率fx=1/2τ=3.03 Hz，相對誤差分別為6.8%和0.73%，在誤差允許范圍內(nèi)。針對基波分量進行分析，可以看出，在次級替代前、后，Hy的變化較大；同時，在表示y方向參數(shù)的式(14) 中，由于β(y0-y1)→0，因此cosh [β(y0-y1)]>sinh [β(y0-y1)]，與Hx相比，μ2r對Hy的影響相對較大。有限元計算結(jié)果與理論分析公式能夠互相證明，表明直線感應(yīng)電機磁場的二維模型滿足自洽性。

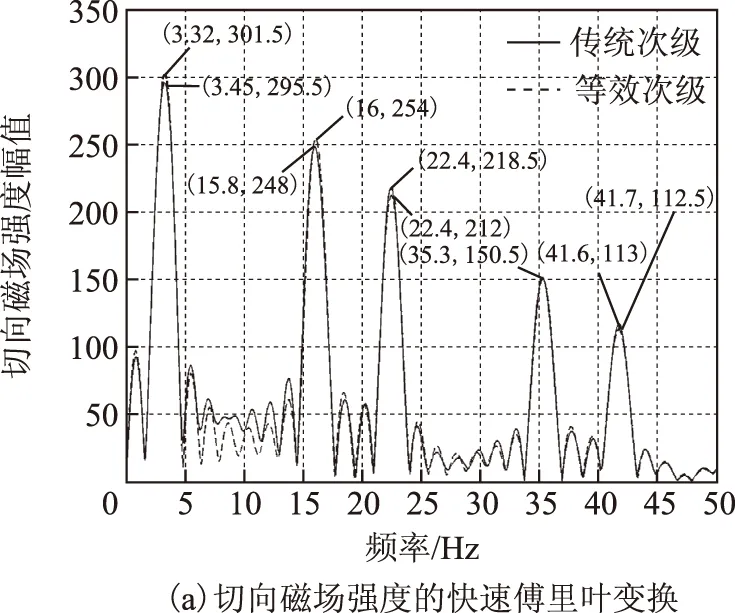
圖6 磁場強度分量快速傅里葉變換結(jié)果Fig.6 The FFT curves of H-components

3 試驗平臺

本文重點針對直線感應(yīng)電機大氣隙的特點，已證明端部效應(yīng)對等效背板的厚度無影響。并且，將直線感應(yīng)電機拖動到空載條件需要額外的原動機以及相當(dāng)大的占地，試驗不易進行；即使采用小型電機(如同步速度4.5 m/s)，受場地和時間限制，實驗精度也難以保證。為此，試驗平臺以異步旋轉(zhuǎn)電機(Rotary Induction Motor，RIM)作為測試對象進行空載試驗測量。待測電機采用YS5614型電機的定子，轉(zhuǎn)子分別為實心鐵轉(zhuǎn)子和軟磁鐵氧體轉(zhuǎn)子，轉(zhuǎn)子直徑均為49 mm，使得電機的氣隙增大2 mm，符合直線感應(yīng)電機大氣隙的特點，具體試驗測量電路如圖7所示。

圖7 空載試驗測量電路Fig.7 The circuit of no-load test

由于電機氣隙遠大于YS5614型電機標(biāo)準(zhǔn)氣隙，空載試驗時初級電流將顯著增加，為避免繞組過熱產(chǎn)生溫升過大甚至燒壞線圈等問題，本文采用曲線擬合的方法進行數(shù)據(jù)處理：輸入電壓最高加至額定電壓 0.8倍左右，并迅速讀數(shù)，數(shù)據(jù)處理采用擬合的方法計算出額定點的電磁參數(shù)。鐵轉(zhuǎn)子和軟磁鐵氧體轉(zhuǎn)子的空載試驗數(shù)據(jù)見表2、表3，其中，U1、IO、PO1、PO2、PO分別為初級電壓、空載電流、第一、二臺功率表的示數(shù)、空載功率。

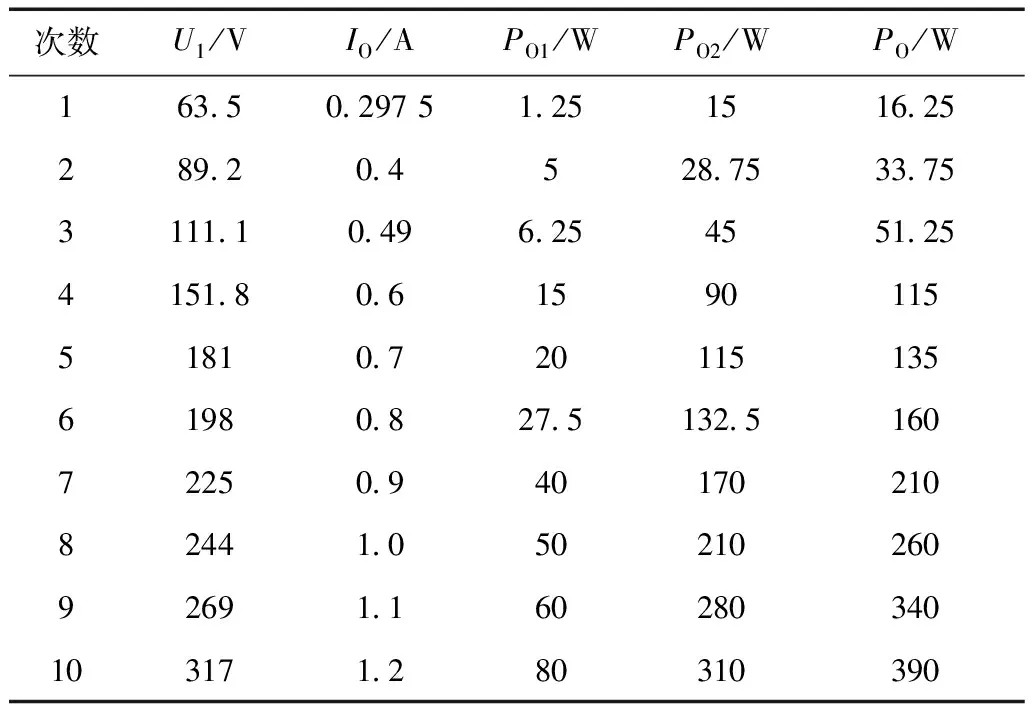
表2 鐵轉(zhuǎn)子空載試驗測量數(shù)據(jù)

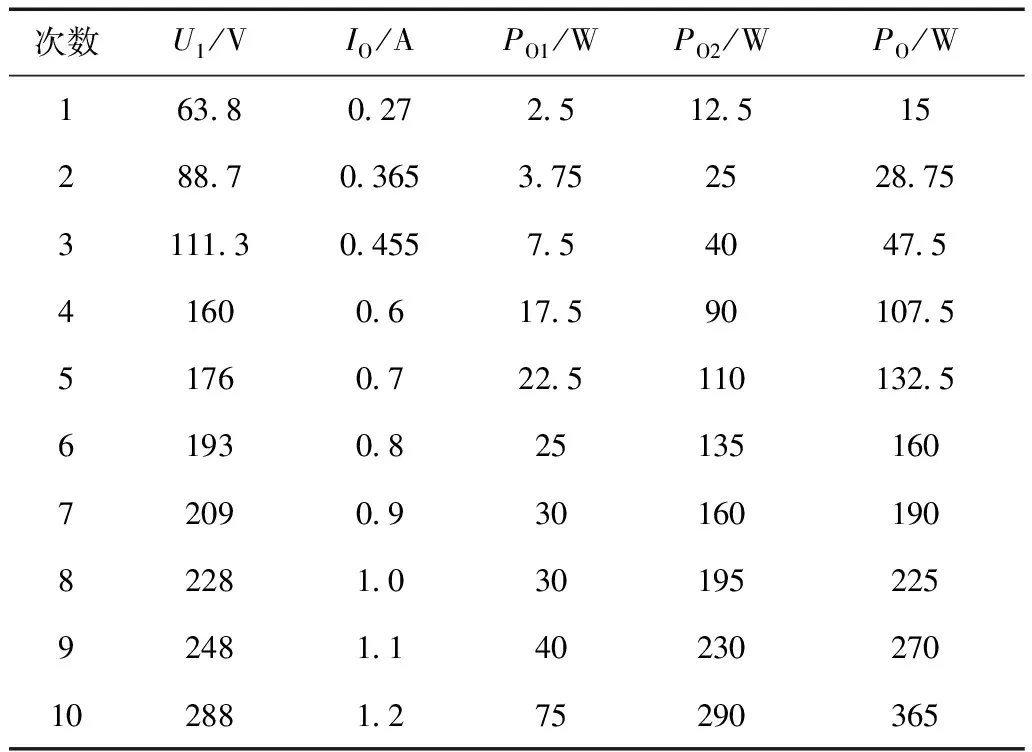
表3 軟磁鐵氧體轉(zhuǎn)子空載試驗測量數(shù)據(jù)

根據(jù)表2、表3，通過Matlab擬合可得圖8曲線。根據(jù)圖8可以推知，額定電壓下，鐵轉(zhuǎn)子電機空載電流為1.47 A，空載功率為589.14 W；軟磁鐵氧體轉(zhuǎn)子空載電流為1.63 A，空載功率為615.73 W。經(jīng)過空載試驗參數(shù)計算，鐵轉(zhuǎn)子電機和軟磁鐵氧體轉(zhuǎn)子電機的勵磁電抗分別為Xm1=63.25 Ω，Xm2=55.12 Ω，因此二者之比Xm1/Xm2=1.147。

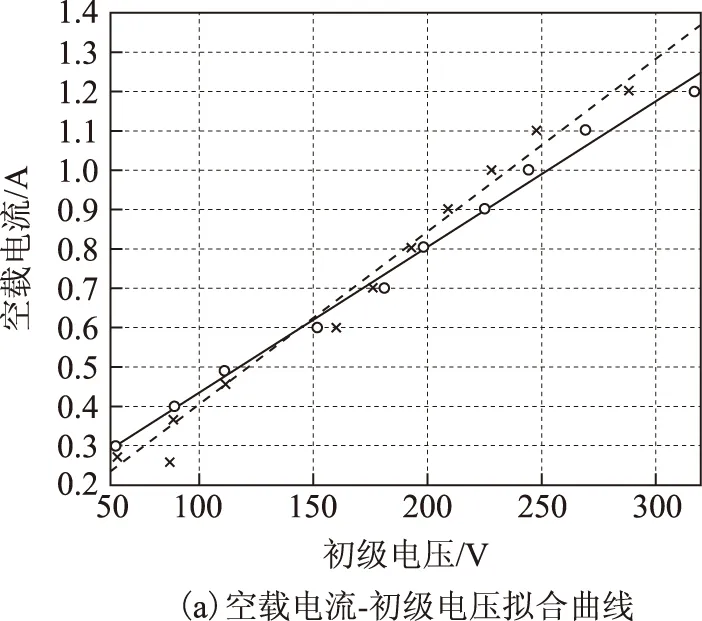
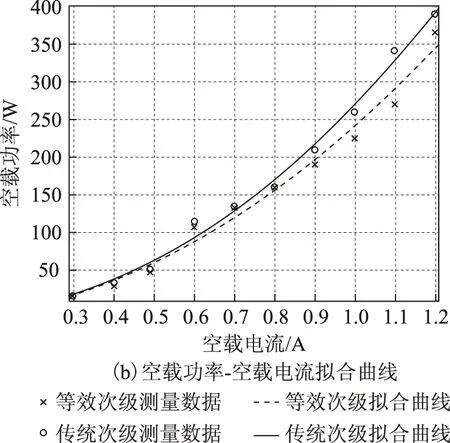
圖8 空載試驗擬合曲線Fig.8 The fitting curves in no-load test

表4為空載試驗勵磁電抗的數(shù)據(jù)對比。為保證數(shù)據(jù)有效性，用于理論計算的直線感應(yīng)電機與YS5614型電機(定子為4極，內(nèi)徑54 mm)具有相同的結(jié)構(gòu)參數(shù)。

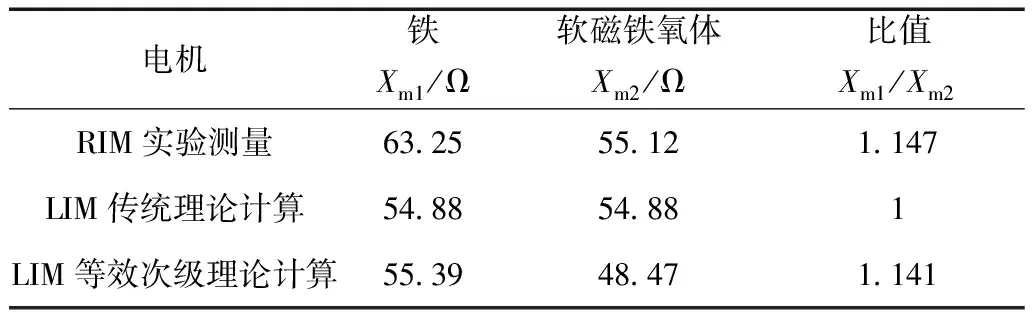
表4 空載試驗勵磁電抗

第二行數(shù)據(jù)采用電機設(shè)計中傳統(tǒng)的磁路計算方法[25]，由于傳統(tǒng)方法認(rèn)為背板材料相對磁導(dǎo)率無窮大，因此其鐵轉(zhuǎn)子電機勵磁電抗Xm1=54.88 Ω準(zhǔn)確有效，而軟磁鐵氧體勵磁電抗Xm2、勵磁電抗比值Xm1/Xm2均不準(zhǔn)確，在數(shù)據(jù)對比中不具有參考價值。

第三行數(shù)據(jù)采用本文提出的等效次級計算方法：根據(jù)前文理論計算，在式(15)中，y0-y1為待測電機的氣隙，y1-y2為將轉(zhuǎn)子沿徑向剖開、拉直后的等效厚度，采用線性化之后的式(20)，求得鐵轉(zhuǎn)子電機勵磁電抗Xm1=55.39 Ω，軟磁鐵氧體轉(zhuǎn)子電機勵磁電抗Xm2=48.47 Ω，二者之比Xm1/Xm2=1.141。

與傳統(tǒng)的磁路計算方法相比，等效次級理論計算的Xm1相對誤差為0.93%，因此可認(rèn)為式(20)真實有效。同時，對于勵磁電抗之比，等效次級理論計算結(jié)果與試驗臺測量結(jié)果相對誤差為0.5%，可以說明，等效次級的折算與端部效應(yīng)的相關(guān)性很小，證明式(21) 真實有效。

由于試驗臺采用的電機在等效到直線電機后，與直線感應(yīng)電機相比，x、y方向上的幾何尺寸差距不明顯，在采用式(20)時條件β(y1-y2)→0、β(y0-y1)→0不夠嚴(yán)格，并且具有端部效應(yīng)帶來的誤差，因此勵磁電抗測量值和傳統(tǒng)磁路計算值有差距，這符合直線感應(yīng)電機的基本理論。由于此項對比與等效次級無關(guān)，因此不會對試驗結(jié)果造成影響。

理論計算與試驗測量相對比，并綜合有限元分析，表明在直線感應(yīng)電機中采用二維電磁場模型進行理論計算是合理的，可以據(jù)此進行直線感應(yīng)電機的等效空載試驗。同時，試驗測量表明，在采用式(20)和式(21)時，要對充分條件β(y1-y2)→0、β(y0-y1)→0進行判定，不過一般地，在直線感應(yīng)電機中，由于其結(jié)構(gòu)特點，這個條件是普遍成立的。

4 結(jié)論

針對直線感應(yīng)電機氣隙大、背鐵中感應(yīng)電流不為零，且電機本體無法與轉(zhuǎn)向架分離的特點，本文提出了一種基于等效次級的直線感應(yīng)電機空載試驗的方法，采用軟磁鐵氧體材料代替背鐵，達到電機次級電流為零的要求，并給出了詳細(xì)的分析過程：

1)建立了直線感應(yīng)電機的電磁場二維模型，對直線感應(yīng)電機大氣隙下的磁場進行了理論分析，根據(jù)此模型得到勵磁電感的解析表達式，計算了次級材料相對磁導(dǎo)率對勵磁電感的影響。

2)依據(jù)直線感應(yīng)電機的幾何結(jié)構(gòu)特點，數(shù)學(xué)上適當(dāng)化簡，使勵磁電感的表達式同時適用于直線感應(yīng)電機的控制。

3)根據(jù)次級材料相對磁導(dǎo)率與勵磁電感的解析表達式，在勵磁電感不變的前提下，計算等效次級的幾何參數(shù)，通過有限元計算與試驗測量驗證，理論計算結(jié)果與測量結(jié)果誤差較小，表明電磁場二維模型真實有效，基于等效次級的空載試驗方法的理論滿足自洽性，為獲得準(zhǔn)確的直線感應(yīng)電機等效電路參數(shù)提供了有效方法。

[1] 宮金林，王秀和.基于多目標(biāo)有效全局優(yōu)化算法的直線感應(yīng)電動機優(yōu)化設(shè)計[J].電工技術(shù)學(xué)報，2015，30(24)：32-37. Gong Jinlin，Wang Xiuhe.Optimal design of a linear induction motor using multi-objective efficient global optimization[J].Transactions of China Electrotechnical Society，2015，30(24)：32-37.

[2] 陳特放，鄧江明，唐建湘，等.磁浮直線感應(yīng)電機的PI自適應(yīng)電流可變轉(zhuǎn)差頻率魯棒控制[J].電工技術(shù)學(xué)報，2014，29(7)：154-162. Chen Tefang，Deng Jiangming，Tang Jianxiang，et al.Variant current variable slip-frequency robust adaptive control for single-sided linear induction motors used in maglev transportation[J].Transactions of China Electrotechnical Society，2014，29(7)：154-162.

[3] 姜杰，王學(xué)斌，殷家敏，等.基于感應(yīng)電動機復(fù)數(shù)簡化模型的參數(shù)辨識研究[J].電力系統(tǒng)保護與控制，2014，42(19)：87-92. Jiang Jie，Wang Xuebin，Yin Jiamin，et al.Research on identification of induction motor based on its simplified complex quantity models[J].Power System Protection and Control，2014，42(19)：87-92.

[4] 孫昊，王茂海，齊霞.基于 PMU 實測數(shù)據(jù)的同步發(fā)電機參數(shù)在線辨識方法[J].電力系統(tǒng)保護與控制，2014，42(3)：31-36. Sun Hao，Wang Maohai，Qi Xia.Synchronous generator parameters identification based on PMU data[J].Power System Protection and Control，2014，42(3)：31-36.

[5] 張宇輝，陳峰，李慧敏，等.基于小波變換和矩陣束算法的同步電機參數(shù)辨識[J].電力系統(tǒng)保護與控制，2012，40(9)：87-92. Zhang Yuhui，Chen Feng，Li Huimin，et al.Parameter identification of synchronous machine based on wavelet transform and matrix pencil algorithm[J].Power System Protection and Control，2012，40(9)：87-92.

[6] 王紅，梁俊霞，胡佳琳.基于αβ坐標(biāo)系模型的雙饋風(fēng)力發(fā)電機參數(shù)辨識[J].電力系統(tǒng)保護與控制，2014，42(20)：81-85. Wang Hong，Liang Junxia，Hu Jialin.Doubly-fed wind power generator parameter identification based on the αβ coordinate model[J].Power System Protection and Control，2014，42(20)：81-85.

[7] 鄧歆，張廣明，王德明，等.基于全階模型的異步電機磁鏈觀測收斂性分析與對策[J].電工技術(shù)學(xué)報，2015，30(1)：61-71. Deng Xin,Zhang Guangming,Wang Deming, et al.Convergence analysis and corresponding strategy of full model based induction motor flux observation[J].Transactions of China Electrotechnical Society，2015，30(1)：61-71.

[8] 黃子果，王善銘，倪守輝.三維分段分層法用于光滑實心轉(zhuǎn)子異步電機參數(shù)計算與性能分析[J].電工技術(shù)學(xué)報，2016，31(23)：15-21. Huang Ziguo, Wang Shanming,Ni Shouhui.Parameter calculation and performance analysis of solid rotor induction machines Using 3D subsectional and multi-layer method[J].Transactions of China Electrotechnical Society，2016，31(23)：15-21.

[9] 徐偉，孫廣生，李耀華，等.一種新型的直線異步電機參數(shù)測量方案[J].電工技術(shù)學(xué)報，2007，22(6)：54-58. Xu Wei，Sun Guangsheng，Li Yaohua，et al.A new parameter measurement scheme for single linear induction motors[J].Transactions of China Electrotechnical Society，2007，22(6)：54-58.

[10]任晉旗，李耀華，徐偉，等.直線感應(yīng)電機在線參數(shù)辨識[J].中國電機工程學(xué)報，2008，28(24)：113-117. Ren Jinqi，Li Yaohua，Xu Wei，et al.Online parameter estimation of linear induction motor[J].Proceedings of the CSEE，2008，28(24)：113-117.

[11]何晉偉，史黎明.一種基于靜態(tài)特性的直線感應(yīng)電機參數(shù)辨識方法[J].電工電能新技術(shù)，2009，28(4)：50-53. He Jinwei，Shi Liming.An identification method for linear induction motor parameter based on static characteristics[J].Advanced Technology of Electrical Engineering and Energy，2009，28(4)：50-53.

[12]Alonge F，Cirrincione M，D′Ippolito F，et al.Parameter identification of linear induction motor model in extended range of operation by means of input-output data[J].IEEE Transactions on Industry Applications，2014，50(2)：959-972.

[13]Sun Zhaolong，Ma Weiming，Liu Dezhi，et al.Modeling and parameter measurement scheme for double primaries coupling linear induction motors[C]//2010 XIX International Conference on Electrical Machines(ICEM)，Rome，2010：1-5.

[14]Kim D K，Kwon B I.A novel equivalent circuit model of linear induction motor based on finite element analysis and its coupling with external circuits[J].IEEE Transactions on Magnetics，2003，42(10)：3407-3409.

[15]Shiri A，Shoulaie A.Design optimization and analysis of single-sided linear induction motor，considering all phenomena[J].IEEE Transactions on Energy Conversion，2012，27(2)：516-525.

[16]Xu Wei，Sun Guangyong，Wen Guilin，et al.Equivalent circuit derivation and performance analysis of a single-sided linear induction motor based on the winding function theory[J].IEEE Transactions on Vehicular Technology，2012，61(4)：1515-1525.

[17]張志華，史黎明，李耀華.柵格次級雙邊直線感應(yīng)電機特性[J].電工技術(shù)學(xué)報，2014，29(3)：103-110. Zhang Zhihua，Shi Liming，Li Yaohua.Characteristics of double sided linear induction motors with ladder-slit type secondary[J].Transactions of China Electrotechnical Society，2014，29(3)：103-110.

[18]秦偉，范瑜，呂剛，等.非磁性次級感應(yīng)懸浮電機磁場和力特性研究[J].電機與控制學(xué)報，2011，15(8)：1-6. Qin Wei，F(xiàn)an Yu，Lü Gang，et al.Characteristic and magnetic field analysis of a non-magnetic secondary induction Maglev motor[J].Electric Machines and Control，2011，15(8)：1-6.

[19]李碩，范瑜，呂剛，等.非磁性次級直線感應(yīng)電機力特性及渦流損耗分析[J].電機與控制學(xué)報，2014，18(4)：1-5. Li Shuo，F(xiàn)an Yu，Lü Gang，et al.Force characteristic and eddy loss analysis of a nonmagnetic secondary linear induction motor[J].Electric Machines and Control，2014，18(4)：1-5.

[20]Ooi B T，White D C.Traction and normal forces in the linear induction motor[J].IEEE Transactions on Power Apparatus and Systems，1970，PAS-89(4)：638-645.

[21]Xu Wei，Zhu Jianguo，Zhang Yongchang，et al.An improved equivalent circuit model of a single-sided linear induction motor[J].IEEE Transactions on Vehicular Technology，2010，59(5)：2277-2289.

[22]劉斌，方進，曹君慈，等.次級結(jié)構(gòu)參數(shù)對高溫超導(dǎo)直線感應(yīng)電機電磁特性的影響[J].低溫與超導(dǎo)，2014，42(5)：46-50. Liu Bin，F(xiàn)ang Jin，Cao Junci，et al.Effect of secondary structural parameters on HTS LIM electromagnetic properties[J].Cryogenics and Superconductivity，2014，42(5)：46-50.

[23]彭威，李偉力，程樹康，等.次級對直線感應(yīng)電動機性能的影響[J].電機與控制學(xué)報，2008，12(1)：47-51. Peng Wei，Li Weili，Cheng Shukang，et al.Influence of secondary on linear induction motor performance[J].Electric Machines and Control，2008，12(1)：47-51.

[24]Li Dong，Li Weili，Cao Junci，et al.Influence of material electromagnetic properties on HTS Linear Induction Motor used in rail transit[C]//2015 International Conference on Electrical Systems for Aircraft，Railway，Ship Propulsion and Road Vehicles(ESARS)，Aachen，Germany，2015：1-7.

[25]上海工業(yè)大學(xué)，上海電機廠.直線異步電動機[M].北京：機械工業(yè)出版社，1979.

(編輯 于玲玲)

Electromagnetic Analysis and Parameter Estimation for the Linear Induction Motor Based on Equivalent Secondary

DiJunFanYuLiuYajing

(School of Electrical Engineering Beijing Jiaotong University Beijing 100044 China)

This paper proposes a method of no-load test for the LIM based on equivalent secondary：back soft ferrite substitutes for back iron to eliminate secondary eddy current while the magnetizing inductance keeps constant.A two-dimensional model of electromagnetic field has been established so as to derive the impact of relative permeability on magnetizing inductance.Keeping the magnetizing inductance constant，the equivalent secondary is designed according to the equation between the relative permeability of the back plate and the magnetizing inductance.The proposed method has been validated via finite element calculation and experimentations.Moreover，the equation of magnetizing inductance has been simplified to some extend in mathematics which can fit the control strategy of the LIM.

Linear induction motor(LIM)，parameter estimation，no-load test，magnetizing inductance

國家自然科學(xué)基金(51077003)和中央高校基本科研業(yè)務(wù)費(2016YJS143)資助項目。

2016-07-21 改稿日期2016-10-20

TM359.4

邸 珺 女，1992年生，博士研究生，研究方向為特種電機及其控制。

E-mail：14117385@bjtu.edu.cn

范 瑜 男，1954年生，教授，博士生導(dǎo)師，研究方向為特種電機及其控制。

E-mail：yfan@bjtu.edu.cn(通信作者)