用層次分析法和模糊評判對整車主觀評價分析

周福庚

ZHOU Fu-geng

安徽江淮汽車集團股份有限公司 安徽合肥230601

用層次分析法和模糊評判對整車主觀評價分析

周福庚

ZHOU Fu-geng

安徽江淮汽車集團股份有限公司 安徽合肥230601

為了對某款新開發重型車的品質進行評價，選定了主觀評價的關鍵指標，應用層次分析法（AHP）確定評價指標的權重。根據駕駛員對整車品質靜態評價和動態測試的結果，對其進行量化處理，通過多級模糊綜合評判，得出了符合實際的評價結論。將主觀評價、層次分析法（AHP）與模糊綜合評判三者有機結合，建立了能夠反映整車品質的評價方法，減少了評價過程中的片面性，評價的結果能夠很好地反映新開發樣車的品質與競品車的對比情況，提高了評價的準確性。

主觀評價 層次分析法（AHP） 模糊綜合評判 指標因素 評判集

1 前言

為了對某新開發的重型車與最新投放市場的同類競品車作對比分析，對整車品質的狀態進行評價，邀請了幾十位有豐富經驗的用戶對其外部造型、內部裝飾等進行靜態主觀評價和通過試乘、試駕對動力性、操縱性、NVH 等進行動態主觀評價，測試者根據自己的經驗與個人感官判斷給出評語。但測試者在評價過程中影響因素較多且具有模糊性，因此需要有進行量化處理的評判方法對整車的品質進行評價。

本文選擇了整車中一些主觀評價的關鍵指標，應用層次分析法（AHP ）確定評價指標的權重[1]，通過模糊綜合評判法[2,3]，將測試者的主觀評價結果進行量化處理，經過多級模糊評判，得出符合實際情況的評價結果。

2 評價指標的權重集建立

在諸多評價指標中，其重要程度各不相同，為了表征各指標對評價目標的影響程度，需要對各指標賦予相應的權重，并組成權重集。確定權重的方法有專家調查法（Delphi 法）、層次分析法（AHP ）、二項系數法、環比評分法、最小平方法等，本文采用層次分析法來確定評價指標的權重。層次分析法(analytic hierachyprocess,AHP)是美國著名運籌學家T.L.Saaty 等人在上個世紀70年代提出的一種定性與定量相結合的多準則決策方法，該方法將定量分析與定性分析結合起來，通過對評價指標相互比較，建立判斷矩陣，給出了矩陣判斷標度（1～9標度法），使矩陣中的各要素的重要性能夠進行定量顯示，進行排序計算等獲得權重集[4]。表1為層次分析法對重要程度的劃分情況。

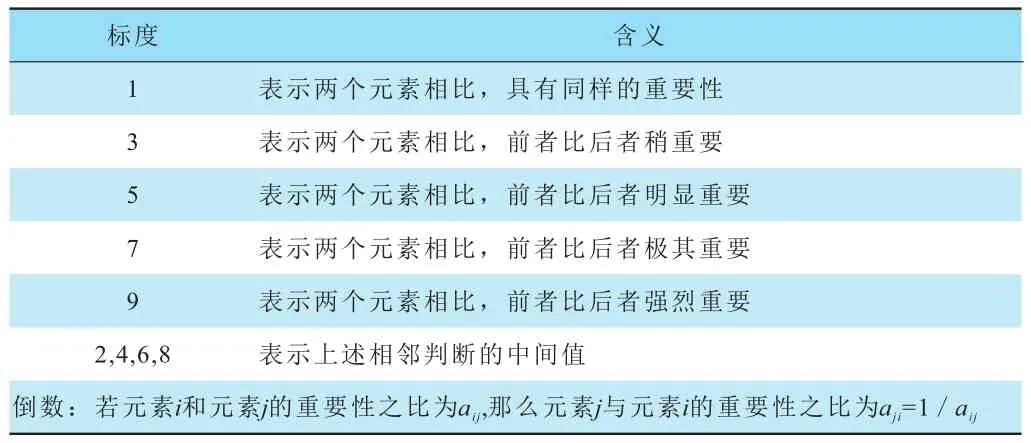
表1 層次分析法的重要程度劃分表

表1反映了兩個評價指標相對重要程度的得分，若評價指標i相對評價指標j的比較分值為aij，則指標j相對i的比較分值為aji= 1/aij。如果認為一樣重要就是1:1，稍重要就是3:1，也可以取中間數值2:1等，兩兩相比較，把數值填入，構造出成對比較判斷矩陣。

汽車的評價指標很多，本文根據評價的需要，列出了能反映整車品質的主要主觀評價指標[4,5]，如表2所示。

對表2的Ⅰ、Ⅱ級指標應用層次分析法確定其權重。

2.1 Ⅱ級指標的權重確定

依據表1中重要程度劃分，對“整車及駕駛室外造型”的Ⅱ級指標構造成對比較判斷矩陣如表3所示。

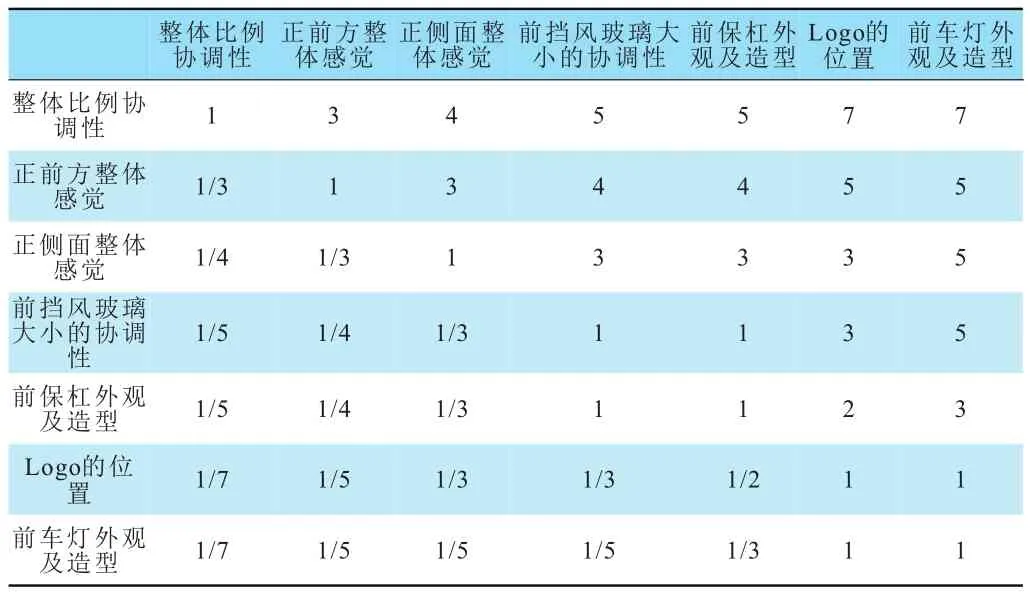
表3 “整車及駕駛室外造型”成對比較判斷矩陣

表2 測評的整車主觀評價指標

由于成對比較矩陣A不是一致矩陣，沒有必要對它作精確的計算，Saaty等人建議用其最大特征根λmax對應的歸一化特征向量作為權向量w。用簡便的近似方法來計算其特征根和特征向量，對于模糊綜合評判完全滿足要求。求最大特征根方法有很多種，本文應用和法來求矩陣A最大特征根λmax。

即得“整車及駕駛室外造型”的Ⅱ級指標權重為：

指標的權重確定是否合理，要對判斷矩陣進行一致性檢驗[2]。

定義一致性指標：

通常計算出值作為最大特征根 λmax的近似值，有：A·w={2.993 1.816 1.098 0.638 0.529 0.290 0.247}T

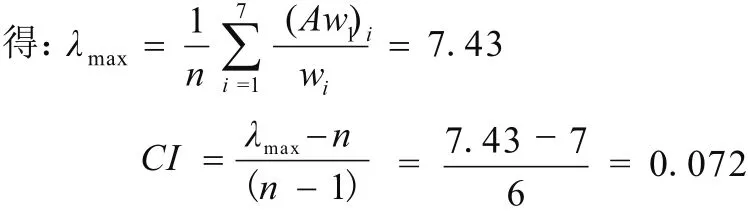
定義：CI=0，有完全的一致性；CI接近于0，有滿意的一致性；CI越大，不一致性越嚴重。由上式知，λ比n大得越多，則矩陣A的不一致性越嚴重，引起的判斷誤差就越大。

再用一致性比率來確定矩陣A的不一致性容許范圍，為了找出衡量矩陣A一致性指標CI的標準，Saaty引入了隨機一致性指標RI，并用樣本計算出了RI的值，如表4所示。

表4 隨機一致性指標RI

定義一致性比率：

查表3得平均隨機一致性指標RI，檢驗矩陣一致性：

一般地，當一致性指標和一致性比率＜0.1時，認為A不一致程度在容許范圍之內，有滿意的一致性，通過一致性檢驗。因此確定的“整車及駕駛室外造型”Ⅱ級指標權重是合理的，滿足模糊綜合評判使用要求。

上述計算中，若一致性指標和一致性比率大于0.1時，要重新構造成對比較矩陣A，對aij加以調整，直到滿足一致性指標和一致性比率＜0.1為止。可見層次分析法（AHP）使定性分析與定量分析有機結合，確定的評價指標權重是合理的。

根據前面的方法，分別構造“駕駛室內部感官”、“整車動態測試”、“駕乘舒適性”、“操縱性能”、“NVH性能”的成對比較判斷矩陣，并求出各Ⅱ級指標的權重如表5～9所示。

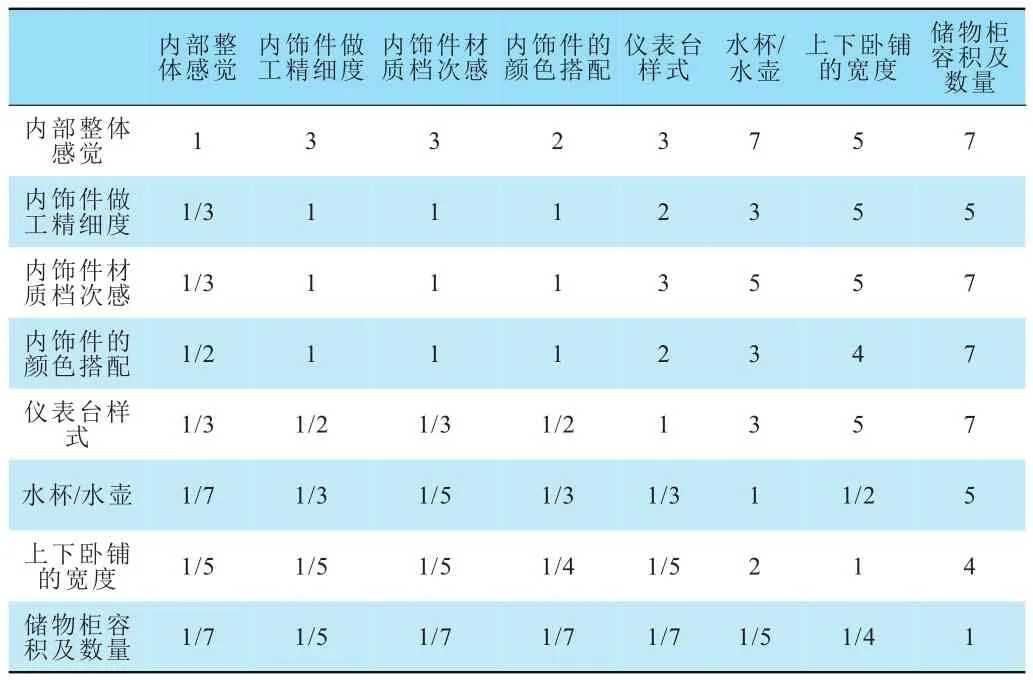
表5 “駕駛室內部感官”成對比較判斷矩陣

計算按上面的步驟，可得權重為：

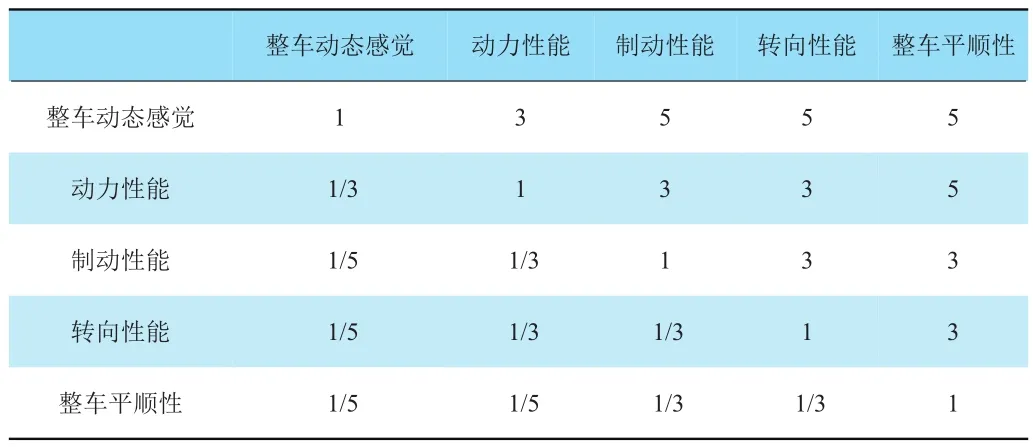
表6 “整車動態測試”成對比較判斷矩陣

得權重為：w={0.543,0.254,0.136,0.076}T

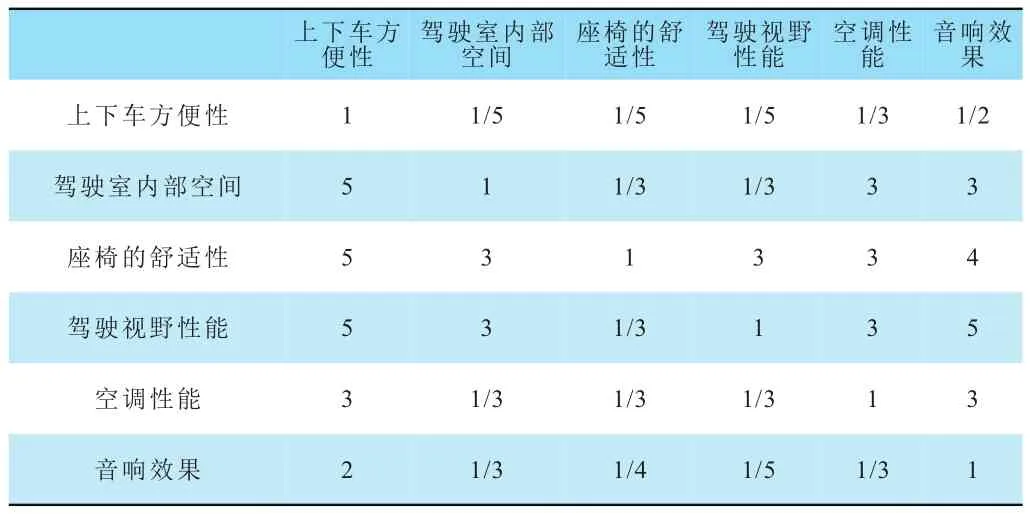
表7 “駕乘舒適性”成對比較判斷矩陣

得權重為：w={0.043,0172,0.357,0.256,0.110,0.062}T

表8 “操縱性能”成對比較判斷矩陣

得權重為：w={0.364,0.256,0.111,0.111,0.111,0.046}T

表9 “NVH性能”的成對比較判斷矩陣

得權重為：w={0.500,0.255,0.125,0.075,0.046}T

2.2 Ⅰ級指標權重確定

整車品質是通過對Ⅰ級指標構造成對比較判斷矩陣如表10所示。

表10 整車的品質成對比較判斷矩陣

得權重為：w={0.377,0.210,0.171,0.139,0.058,0.045}T

對表5～10的判斷矩陣進行一致性檢驗，CI和CR值均小于0.1，判斷矩陣都通過了一致性檢驗。

至此，整車Ⅰ、Ⅱ級評價指標的權重集均確定下來，且得出的結果已作歸一化處理。

3 模糊綜合評判數學模型及評價方法建立

多級模糊綜合評判數學模型及評價方法的建立在文獻[6]中有了詳細的敘述，在此簡要說明。

3.1 模糊綜合評判數學模型建立

3.1.1 評價指標集確定

假設對汽車的評價指標有n個，記為：x1，x2，x3，…，xn；則這n個評價指標構成了一個指標因素集合。記為：

3.1.2 評價等級集確定

由于每個指標的評價不同，形成了不同的等級，將評價的等級劃為m個，記為：y1，y2，y3，…，ym；這m個評價等級構成了一個評價等級集合也稱評語集。記為：

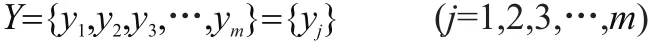
3.1.3 各評價指標權重的確定

應用層次分析法確定各評價指標權重。

3.1.4 模糊綜合判斷矩陣建立

通過指標集合X中的指標因素xi(i=1,2,3,…,n)和評價等級yj(j=1,2,3,…,m)，確定指標的評判模糊子集為：

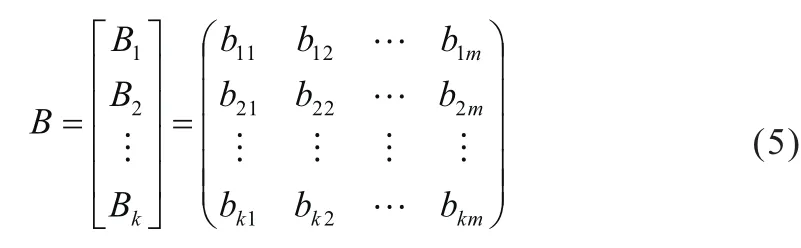
由n個指標因素評判模糊子集組合起來，構造出了一個總的模糊綜合評判矩陣R：

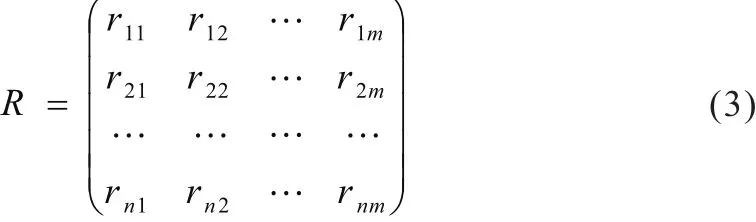
R為從X到Y的一個模糊關系的 n×m階矩陣，其元素rij(i=1,2,3,…,n，j=1,2,3,…,m)表示評價等級yj對 指標xi所作的評判，且有0≤rij≤1。

3.1.5 綜合評判

通過X的權重集合w與模糊關系矩陣 R=(rij)n×m進行模糊變換，就可得到綜合評判集合B，即

上式為模糊綜合評價的數學模型，B為模糊綜合評價的結果，是一個m維模糊行向量。

可用普通矩陣的乘法運算法則進行運算，求綜合評判集合 B，則有：并將B模糊子集作歸一化處理，即且有 bj∈[0,1]。

3.2 多級模糊綜合評判的方法

對于汽車產品，評判的系統影響因素很多，僅由一級評判不能很好地反映汽車的真實品質，則需要進行二級或多級綜合評判。

3.2.1 初級模糊綜合評判模型

它同時也是高級模糊綜合評判的指標矩陣。

3.2.2 高級模糊綜合評判

基于初級模糊綜合評判矩陣B，進行高級模糊綜合評判，評判結果為：

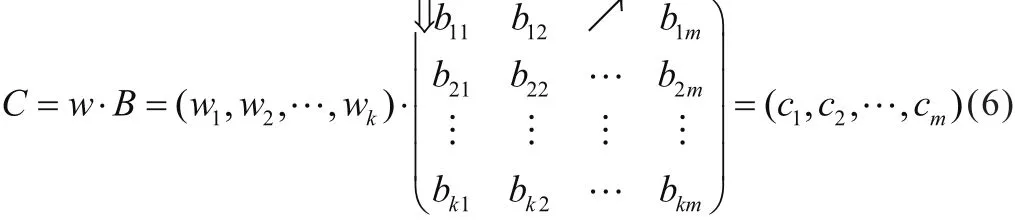
同樣它是一個m維的模糊綜合評判行向量，式中ci=

3.2.3 評判指標的處理

為使得出的綜合評價結果具有可比性，對ci歸一化處理，即且 c∈[0,1]。用最大隸屬度法，取向量C中最大值i作為評判結果。

4 開發樣車主觀評價的多級模糊綜合評判

依據整車主觀評價指標，確定了模糊綜合評判的Ⅰ級評價指標集相應地其各指標集的子集對應Ⅱ級指標，指標集及各子集的權重用層次分析法確定。在評判過程中，先評判Ⅱ級指標，再評判Ⅰ級指標。

4.1 建立整車評價等級集

評價等級集是一個Ⅸ維向量的評語集，Ⅰ、Ⅱ級主觀評價指標評語集均表示為評價等級集合可用{非常好，很好，好，較好，一般，較差，差，很差，非常差}來表示。

4.2 初級模糊綜合評判

為了客觀地了解新開發的牽引車品質（記為“開發樣車”），選擇了最新上市的，代表著國內重卡水平的某兩款不同品牌牽引車（分別記為“競品車甲”、“競品車乙”）。邀請了30位重卡經銷商和用戶對三臺車進行測評，按“整車及駕駛室外造型”和“駕駛室內部感官”的各項指標進行靜態主觀評價；在30位中抽取了20位有非常豐富駕駛經驗的用戶分別按“駕乘舒適性”、“操縱性能”、“NVH性能”、“整車動態測試”等各指標進行動態評價，要求用戶對每項指標按“非常好，很好，好，較好，一般，較差，差，很差，非常差”九個等級評語進行判定。由于都是最新產品，從用戶評價表中發現，他們給出的評語基本都在“非常好”和“一般”之間，只有個別用戶對“牽引車乙”某兩項指標給了“較差”評語。為了分析方便，在評價中將此評語歸到“一般”中，這對評價結果沒有任何影響。

據此，把原Ⅸ維向量的評語集調整為{非常好，很好，好，較好，一般}的Ⅴ維向量評語集，減少了分析的工作量。

將三輛車Ⅱ級各評價指標的Ⅴ維向量評語進行歸一化處理，分別如表11～16所示。

從表11中抽取“開發樣車”的各指標子集，可構建其評判集的隸屬矩陣為：

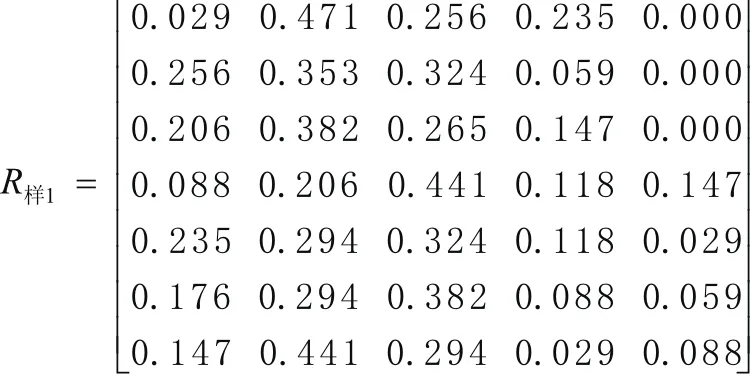
根據公式(4)，用普通乘法算子法，得到對Ⅰ級指標“整車及駕駛室外造型”的綜合評判集合為：

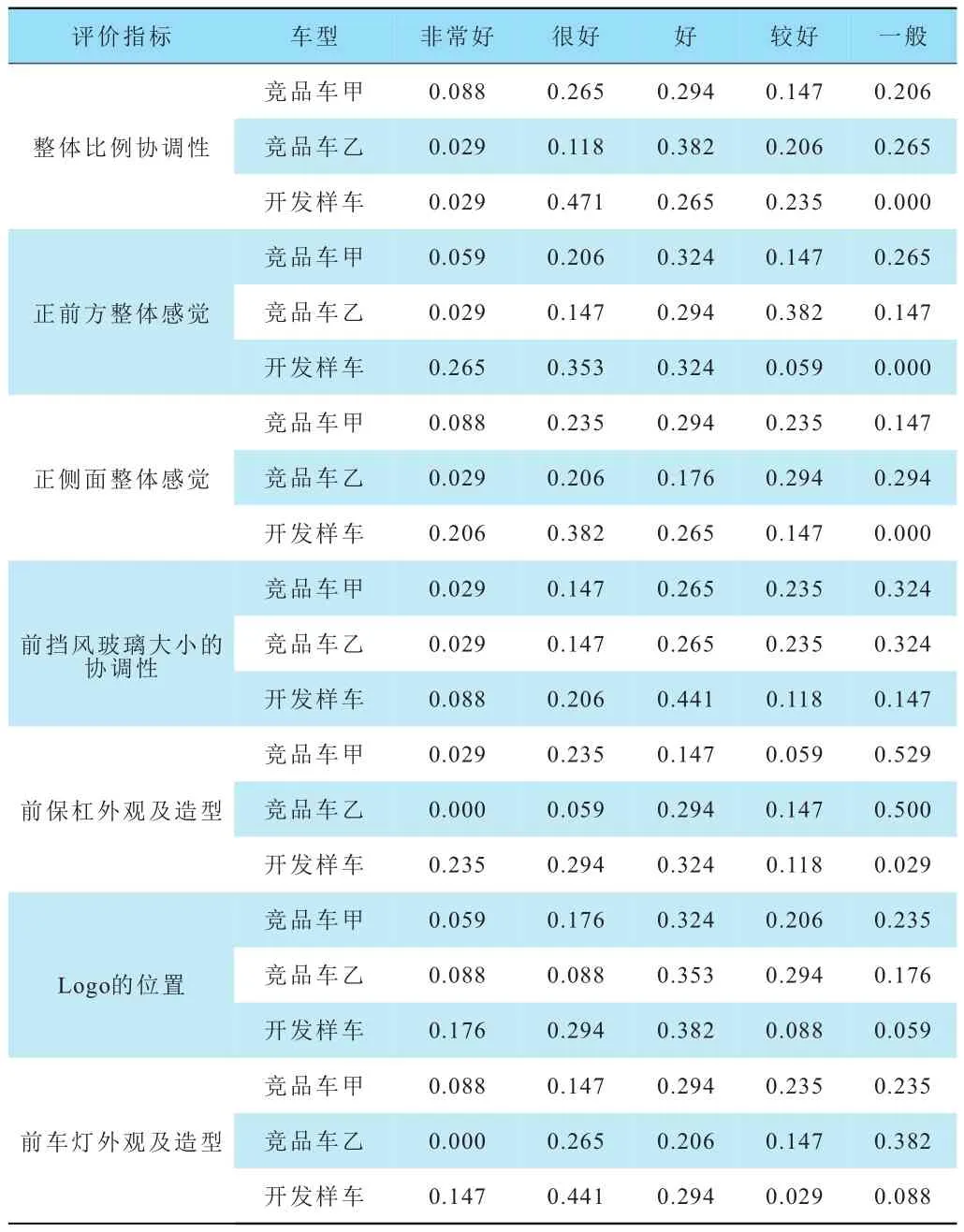
表11 “整車及駕駛室外造型”評價結果歸一處理

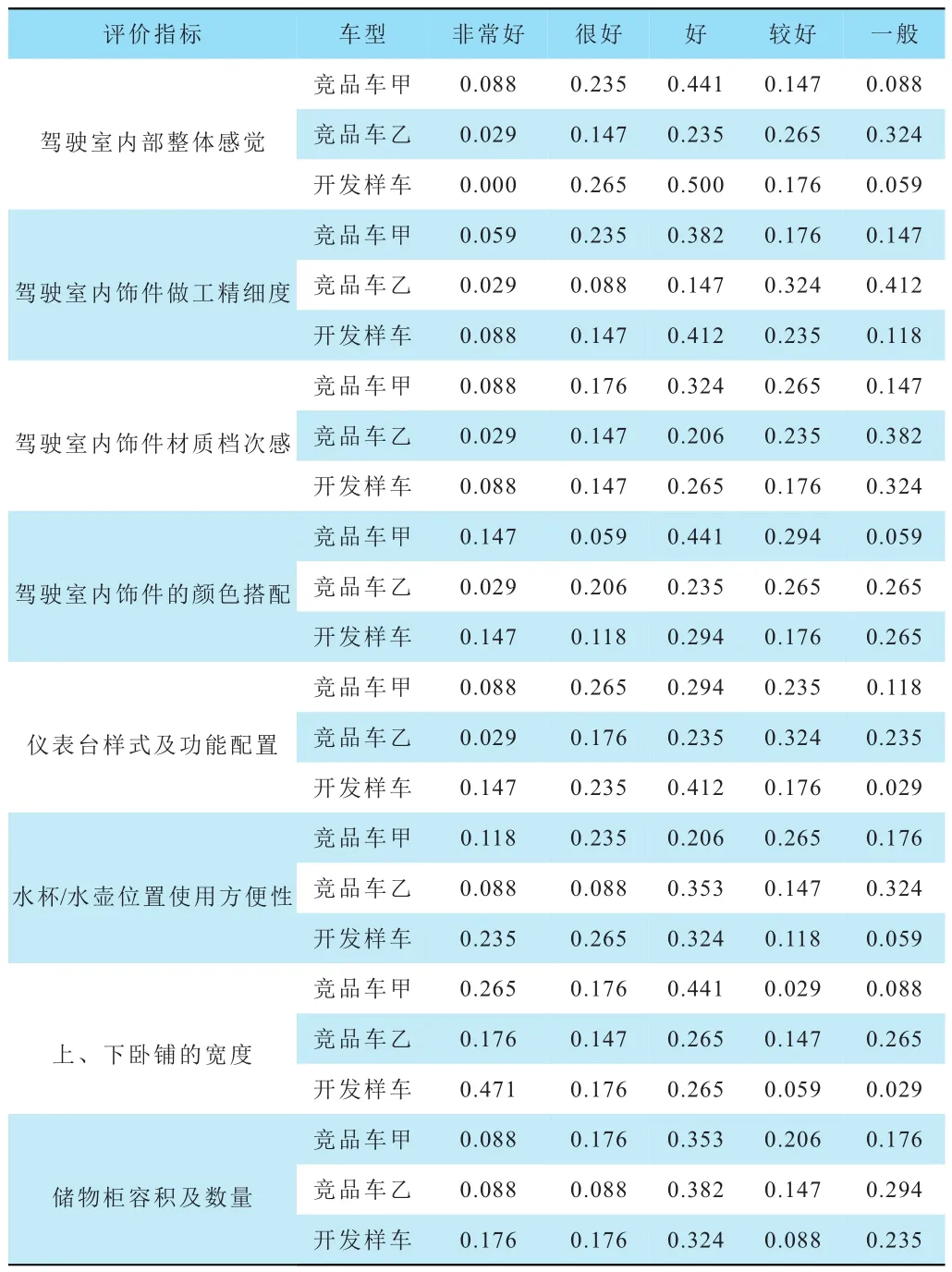
表12 “駕駛室內部感官”評價結果歸一處理

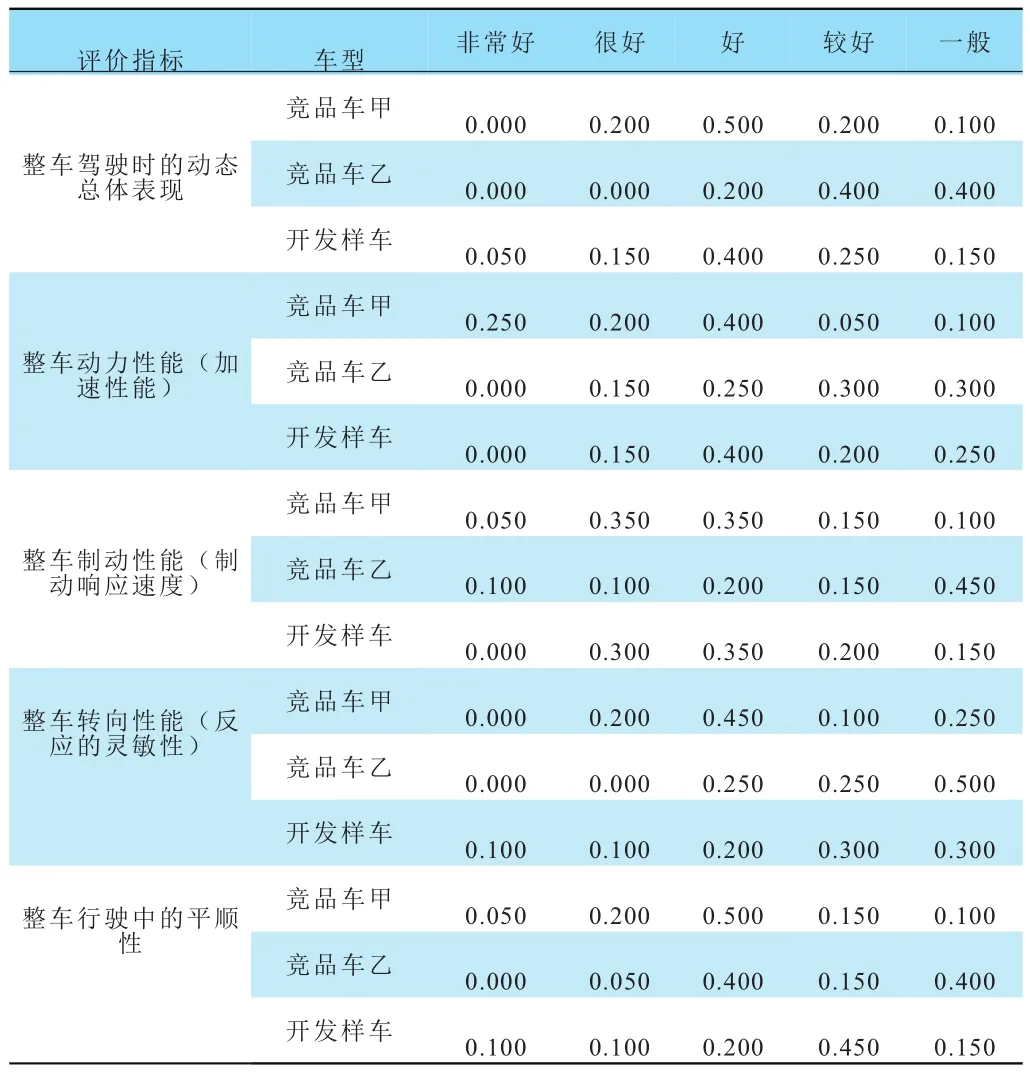
表13 “整車動態測試評價”評價結果歸一處理

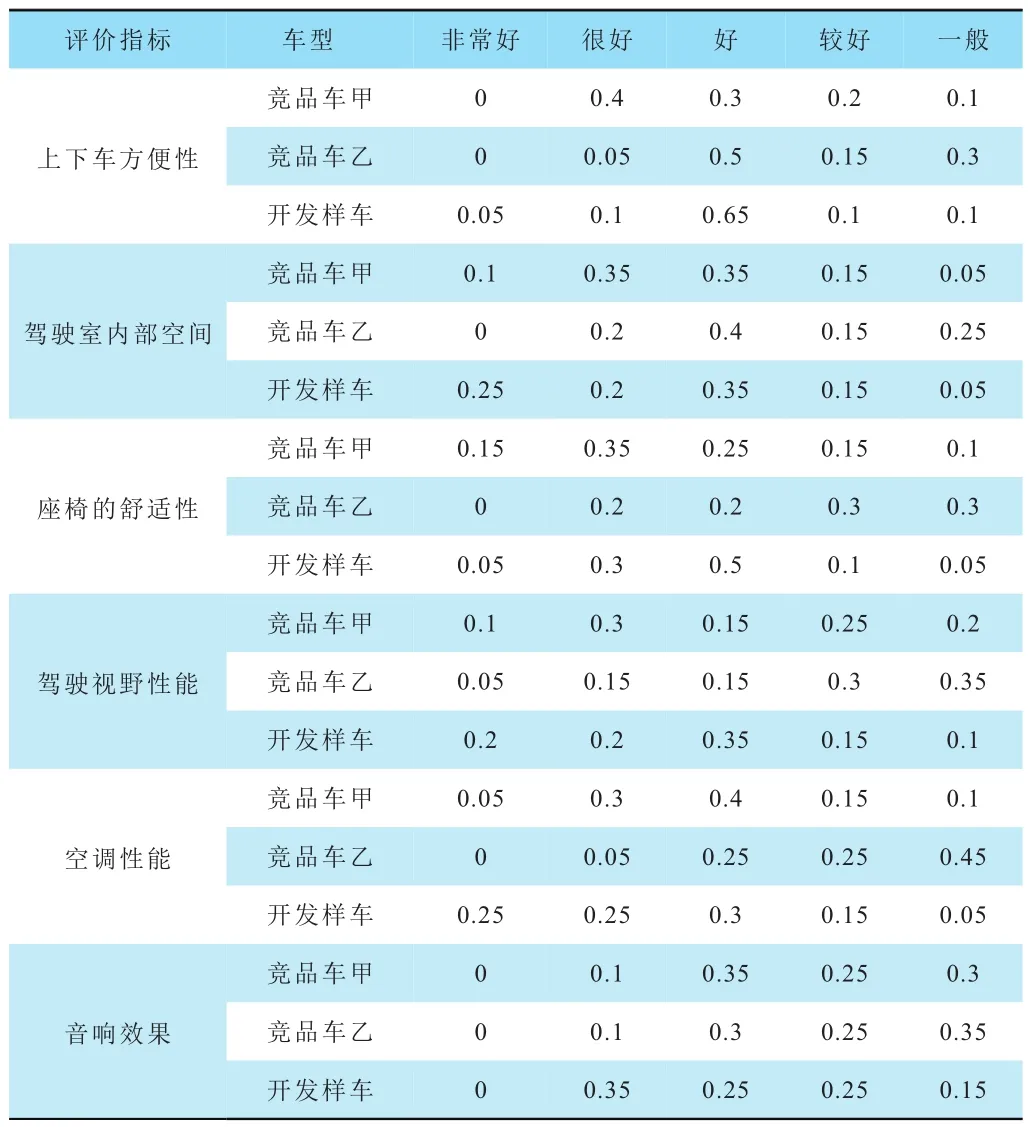
表14 “駕乘舒適性”評價結果歸一處理

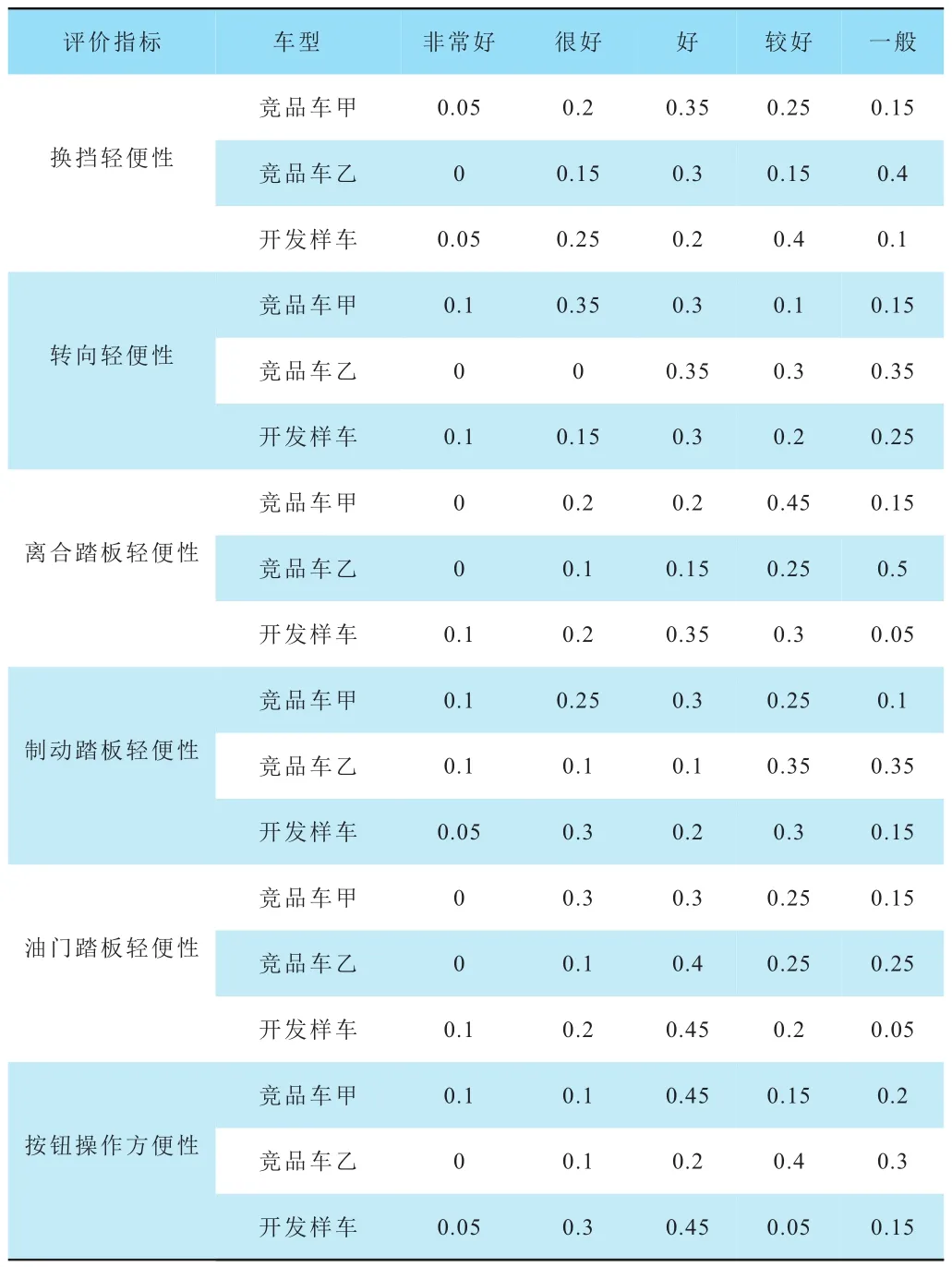
表15 “操縱性能”評價結果歸一處理

根據最大隸屬度法則，三輛車六項Ⅱ級評價指標評價結果如表17所示。

4.3 二級模糊綜合評判

二級模糊綜合評判基于一級模糊綜合評判的結果，對整車的品質進行綜合評判，可構建評判集B的隸屬矩陣為：

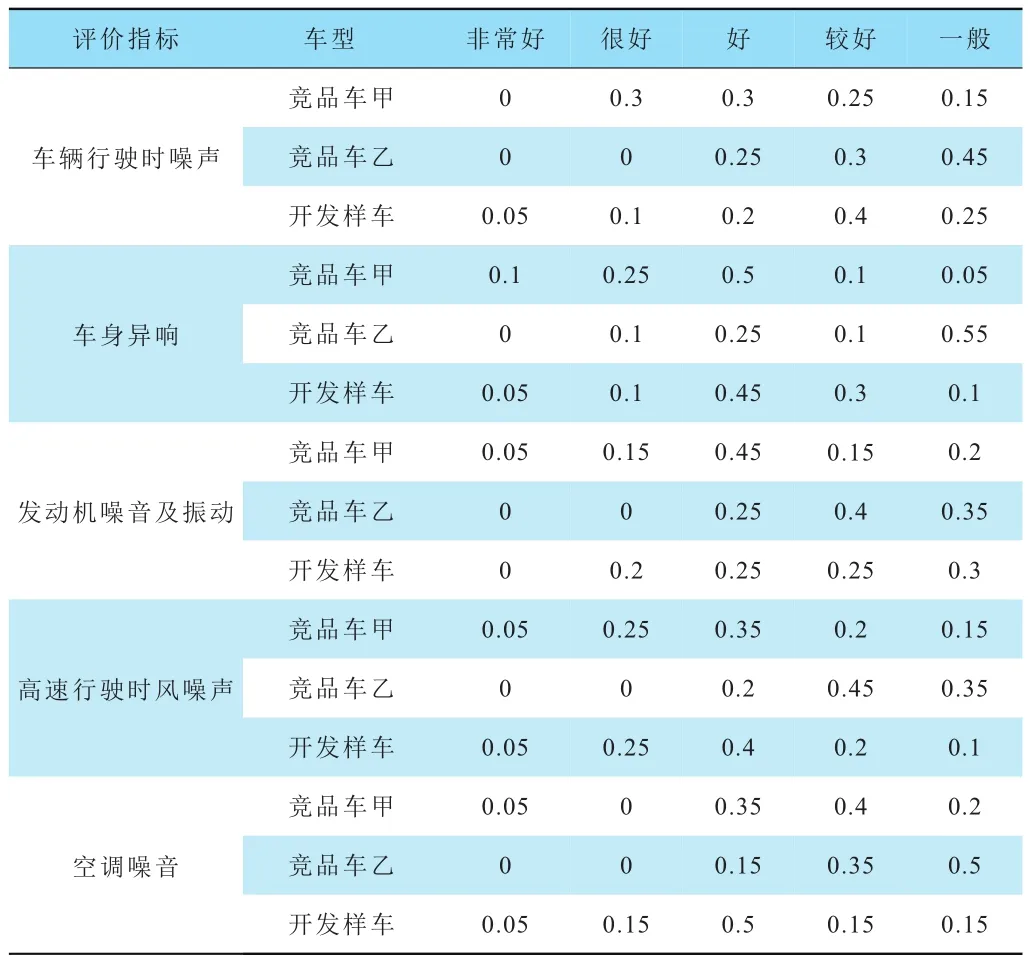
表16 “NVH性能”評價結果歸一處理

表17 三輛車六項Ⅱ級評價指標評價結果

根據公式(6)求得：

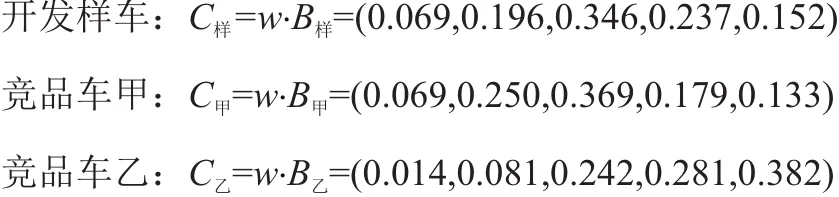
根據最大隸屬度法則，開發樣車和競品車甲整車的品質是“好”，競品車乙是“一般”。

為了便于比較，可以用分值來作評判，根據模糊評價集Y={非常好，很好，好，較好，一般}={100，90，80,70,60}。有：

用分值評判這三輛車的總體品質均在“好”與“較好”之間，競品車甲整車的品質是最好，接近“很好”，開發樣車次之，但兩者差別不大，競品車乙略差于前兩輛。

5 結語

通過對用戶的測評結果進行評判分析，開發的牽引車僅在“好”和“較好”之間，與設定的目標“非常好”有較大的差距，一些指標不如競品車。評判出有差距的指標，對產品品質的提升及整改提供了明確的方向。

采用層次分析法（AHP）來確定評價指標的權重，使定性分析與定量分析有機結合，可以避免因人的主觀性導致權重預測與實際情況相矛盾現象，提高了權重集的合理性。前面的分析可知，所確定的評價指標權重是合理的。

文章將主觀評價、層次分析法（AHP）與模糊綜合評判三者結合，建立了反映整車品質的評價方法，減少了評價過程中的片面性，評價的結果能夠真實地反映新開發車的品質及與競品車的對比情況，提高了評價的準確性。

[1] 許樹柏.層次分析法原理[M].天津:天津大學出版社,1988.

[2] 謝季堅,劉承平.模糊數學方法及其應用[M].武漢:華中科技大學出版社,2000.

[3] 張聽,楊志軍,用模糊綜合評判法評價汽車綜合性能[J].機械, 2003.30 (1):27-28.

[4] 張炳江.層次分析法及其應用案例[M].北京:電子工業出版社,2014.

[5] 劉濤,畢傳興,張永斌.基于模糊綜合評判的汽車整車品質評價指標的研究[J].合肥工業大學學報,2011.34 (10):1457-1460.

[6] 周福庚.基于模糊綜合評判對某商用車主觀評價結果分析[J].專用汽車, 2014 (11):108-112.

[7] 鐘利軍,劉繼廣,田占會.基于模糊綜合評判的轎車綜合性能評價方法[J].汽車科技, 2008 (4):31-33.

UEvsianlgu aAtinoanl yAtinca Hlyiseirsa frocrh Vy ePhrioccleess (AHP) and Fuzzy Evaluationof Subjective

The article selected the subjective evaluation of key indicators, using analytic hierarchy process (AHP) to determine the weights of evaluation indexes. According to the driver of vehicle quality the results of static evaluation and dynamic test, carries on the quantitative processing, through the multistage fuzzy comprehensive evaluation, the practical evaluation conclusion. The subjective evaluation, the analytic hierarchy process (AHP) and fuzzy comprehensive evaluation of organic combination, established the reflect vehicle quality evaluation method, reduces the partial surface in the process of evaluation, evaluation results can well reflect the quality of the new development of a prototype and competing goods vehicle contrast situation, improve the accuracy of the evaluation.

subjective evaluation; analytic hierarchy process (AHP); fuzzy comprehensive evaluation; index factors; judge set

周福庚，男，1964年生，研究員級高級工程師，主要從事汽車產品設計開發和研究工作。

U462.2

A

1004-0226(2017)06-0097-08

2017-03-07