一種適用于多個可轉位刀片的周邊刃邊緣檢測方法

陳宇彤，葉軍君，陳彬強，孫維方，李凌祥

（1.廈門大學航空航天學院，福建廈門361005；2.廈門金鷺特種合金有限公司，福建廈門361000）

一種適用于多個可轉位刀片的周邊刃邊緣檢測方法

陳宇彤1，葉軍君1，陳彬強1，孫維方1，李凌祥2

（1.廈門大學航空航天學院，福建廈門361005；2.廈門金鷺特種合金有限公司，福建廈門361000）

針對可轉位刀片周邊刃邊緣檢測的問題，提出了一種適用于多個可轉位刀片的基于局部模糊檢測和雙樹復小波變換的邊緣檢測算法。該算法主要分為兩步，第一步是先按事先規定的要求拍攝可轉位刀片的圖片，然后對拍好的圖片進行局部模糊檢測處理，其中的檢測算法是以圖片中像素的相關性系數和基于Laplacian算子的新型判別算子為評價指標判斷其是否位于模糊區域（若位于模糊區域，則用白色顯示它，反之，則用黑色顯示）。模糊檢測算法在剔除誤檢像素后最后會生成一副二值圖，可轉位刀片的周邊刃邊緣即為二值圖中黑色區域和白色區域的交界線。第二步就是用雙樹復小波變換對二值圖進行邊緣檢測，檢測后的結果就是我們需要的結果。實驗結果證明，該算法能準確快速地檢測出多個可轉位刀片的周邊刃邊緣。

可轉位刀片；周邊刃；邊緣檢測；局部模糊檢測；雙樹復小波變換

在現代制造技術中，可轉位刀具作為高檔刀具發揮著越來越重要的作用，可轉位刀片作為可轉位刀具的關鍵功能元件，其周邊刃加工精度對可轉位刀具的切削效率有著重要的影響，而提高可轉位刀片加工精度就需要先對周邊刃刀片幾何參數進行準確測量，故提高可轉位刀片的檢測水平，對于生產可轉位刀具有著極其重大的意義。目前，國內外常用的測量方法主要分為兩類：接觸式測量和非接觸式測量[1]。接觸式測量測量方式簡單直觀，但會有側頭磨損引起的誤差，要備有防損傷措施的低速低效運動。隨著制造技術的發展，這種測量方法已無法滿足現代制造的需求，故高效、高精度、無損傷的非接觸式測量方法應運而生，這其中應用到刀片測量的主要有光學測量法。它利用光學原理對刀片表面輪廓形狀進行測量，具有精度高、速度快等優點。其測量方式也是多種多樣，有激光三角法、干涉測量法、圖像測量法等等[2]。本文對可轉位刀片幾何參數進行測量采用的是圖像測量法，其第一步也是最關鍵的一步就是對可轉位刀片周邊刃的邊緣進行檢測，因為圖像邊緣反映了圖像的最基本特征，是圖像信息最集中的地方[3]。

在機器視覺中，邊緣被定義為圖像中灰度發生劇烈變化的像素點所構成的集合。對于特定的圖像，傳統邊緣檢測方法主要有Robert算子、Sobel算子、Canny算子、Laplacian算子等。每種算子特點各異，且適用范圍不盡相同[3]：Robert算子和Sobel算子是一階微分檢測算子，梯度計算相對簡單，但對噪聲較敏感，抗噪能力較差，容易將噪聲誤檢測為邊緣；Canny算子、Laplacian算子是二階微分檢測算子，Laplacian算子對噪聲很敏感，故常常采用對Laplacian算子進行改進后的LOG算子[4]；Canny算子因其具有較好的檢測質量，且有定位精度高、誤判率低等這些特點，故被認為是目前最成功的和使用最廣泛的邊緣檢測方法之一[5]。

目前，針對可轉位刀片的邊緣檢測算法有個共同的不足就是只能對一塊刀片進行檢測，還無法同時檢測同一圖片下多個刀片的邊緣，且在圖片受到噪聲嚴重污染時檢測精度將會受到很大的影響，所以有必要提出一種更行之有效的檢測算法。由相機的成像原理可知，位于相機景深范圍之內的物體點在照片上形成清晰的像點，而位于景深范圍外的則形成模糊的像點。根據這個原理，在對刀片進行拍照時，可以選用景深較小的攝像頭（因為刀片厚度小）使得刀片的前刀面本身成像成清晰的區域，而其他地方成像成模糊的區域（即照片的背景），這樣可轉位刀片的邊緣就是清晰區域和模糊區域的分界線。鑒于此，本文將提出一種基于局部模糊檢測和雙樹復小波變換的邊緣檢測算法，其中局部模糊檢測采用了結合頻域自相關系數[6]和基于Laplacian算子的新型判別算子來判斷圖像中的像素位于模糊區域或者清晰區域的新算法。此邊緣檢測算法不僅僅適用于單個刀片，還可以把它運用到同一圖片下的多個刀片，工業上具有廣闊的應用前景。更重要的是，實驗結果表明該算法能準確快速的檢測出多個刀片的邊緣。

1 局部模糊檢測

1.1 圖像模糊的數學模型

模糊圖像在數學上一般可以表示為初始清晰圖像和模糊函數（點擴散函數）的卷積，具體的公式如下所示：

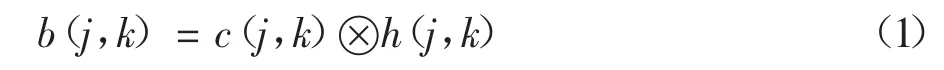
這里b（j，k）（（j，k）∈Db），c（j，k）（（j，k）∈Dc）分別表示模糊圖像和初始清晰圖像，h（j，k）（（j，k）∈Dh）表示模糊函數（點擴散函數），Db、Dc、Dh分別為它們的定義域。

1.2 自相關系數[6]

假設c1（j，k），c2（j，k）分別為模糊圖像中兩個大小相等的隨機塊，它們的初始清晰圖像塊是b1（j，k），b2（j，k），則由公式（1）可得：

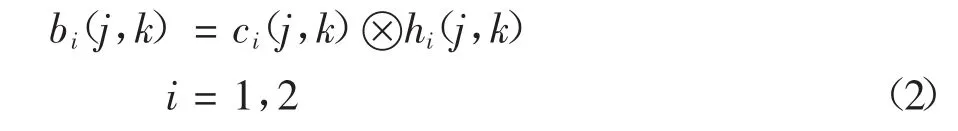
對公式（2）兩邊做傅里葉變換并同取絕對值，得:

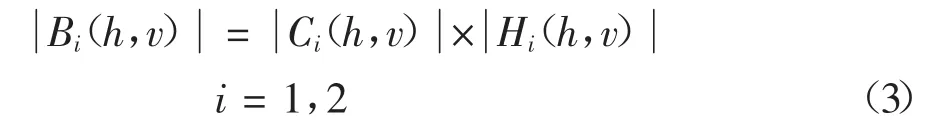
最后對公式（3）兩邊取對數，得：

其中Corr（·）為兩矩陣的相關性系數，即

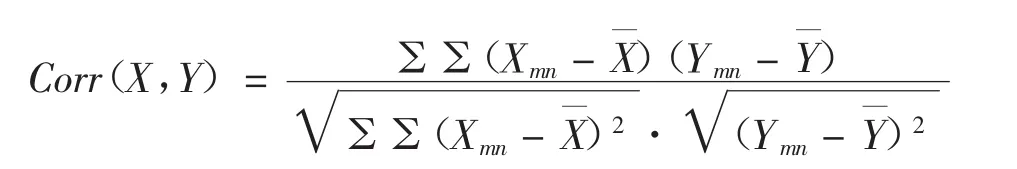
式中：Xmn、Ymn分別為矩陣X和Y的各元素X軍、Y軍為X和Y的平均值。

由關系式（6）可知：相關性系數是描述兩個量之間的線性相關程度，局部模糊區域中的像素由于像素的重疊，故模糊區域內的像素一般具有較大的相關性系數，而其他較為清晰的區域則一般相關性系數較小。至此，就可以把整張圖像的像素劃分為兩類：（j，k）∈R1為模糊部分，（j，k）∈R2為較清晰部分。判斷點（j，k）是屬于R1還是R2的具體算法如下：

（1）先把以（j，k）為中心的大小為（2N-1）×（2N-1）的矩形領域平均分為四小塊（X1，X2，X3，X4），每小塊的大小為N×N，具體如圖1所示。

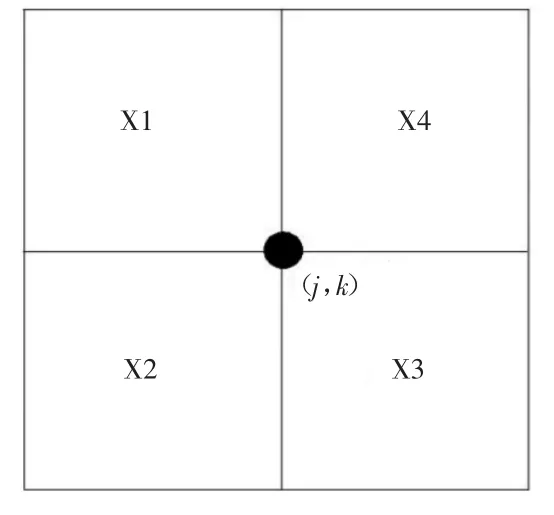
圖1 局部領域塊的劃分

（2）計算各塊對應的頻域對數系數X軒1（h，v），X軒2（h，v），X軒3（h，v），X軒4（h，v），然后再計算對角領域塊的相關性系數:

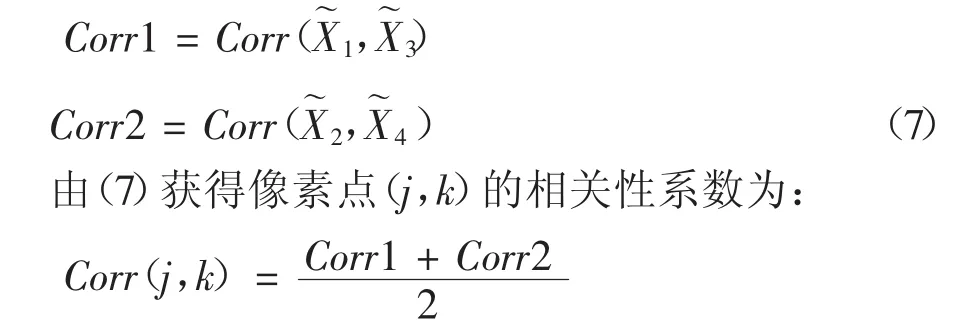
（3）將Corr（j，k）同預設的閥值C1作比較，并根據比較結果生成二值圖B.若Corr（j，k）>C1，則像素點（j，k）∈R1，B（j，k）＝1；反之，則像素點（j，k）∈R2，B（j，k）＝0.

1.3 基于Laplacian算子的判別算子

由圖像處理的知識可知，Laplacian算子值的大小可以直接反映相鄰像素間灰度變化的快慢。局部模糊區域中相鄰像素間的灰度變化往往比較緩慢，而清晰或者含銳利邊緣的區域相鄰像素間的灰度變化則相對較快。基于這一點，可以通過改造拉普拉斯算子而得到一個新的算子來判定模糊。下面開始定義這個算子，并逐步說明具體的判定算法。

首先，在以像素（j，k）為中心、大小為K×K的矩形領域S內，定義如下算子：

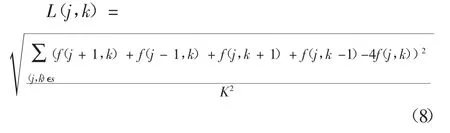
其中，K為奇數，f（j，k）為像素（j，k）的灰度值。

接著，設整副圖像像素區域T的大小為M×N.在T內再定義一個類似于（8）式的全局算子：

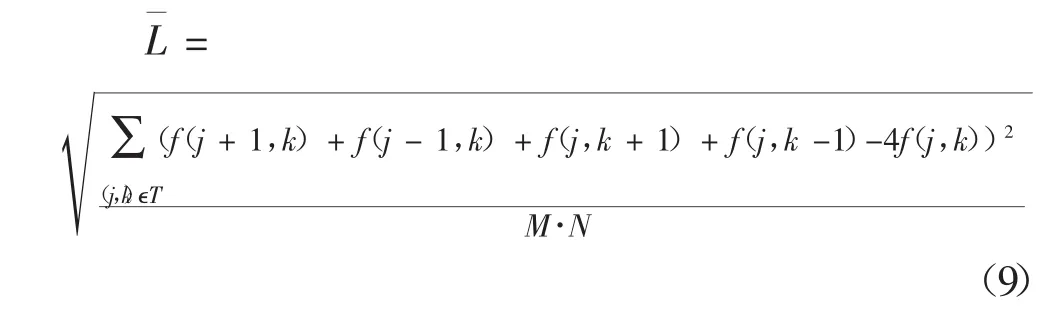
最后，為了減小誤差，采用（10）式作為像素（j，k）的模糊測度：

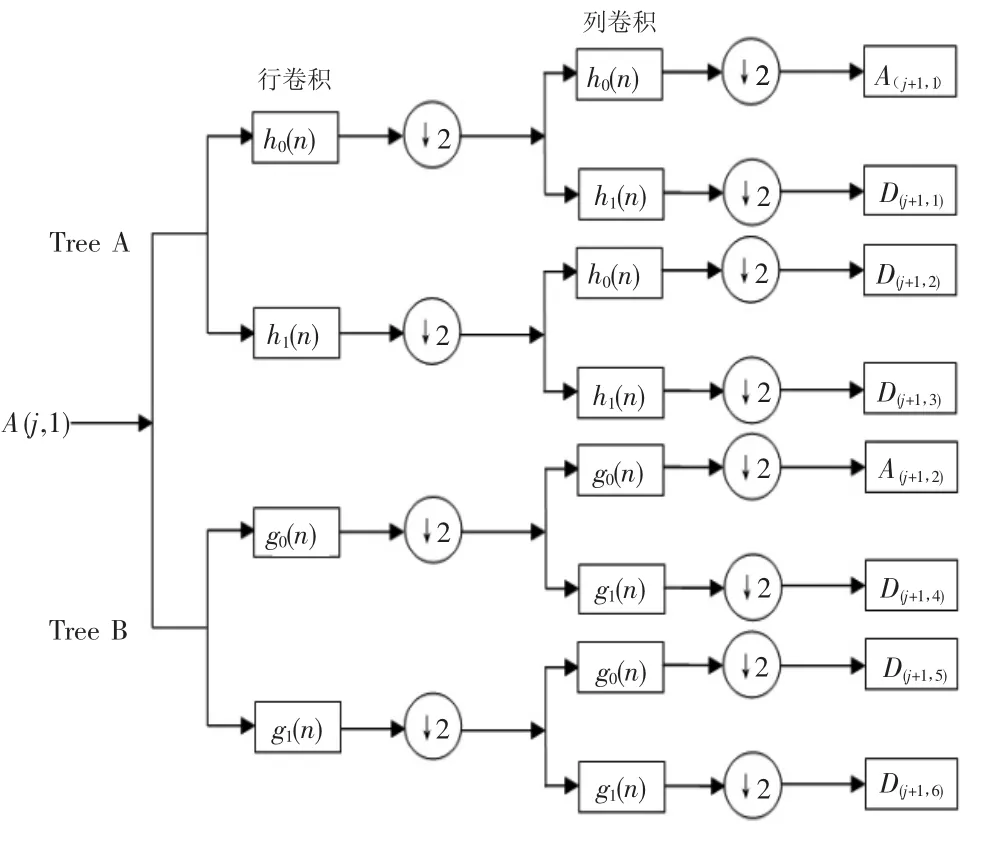
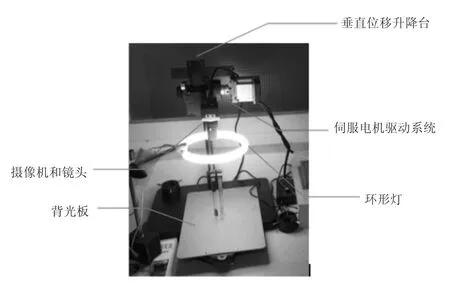
設T1為預設的閥值，當q

1.4 模糊區域檢測算法

由于圖像的具體類型是多種多樣的，所以單獨使用自相關系數或者基于拉普拉斯算子的新型判別算子來判定模糊帶有一定的局限性，檢測效果往往也不盡如人意。故有必要把這兩個模糊指標結合起來共同判定模糊以獲得更好的檢測效果。根據最終判決結果生成的二值圖B，可以認為白點聚焦較多的區域為模糊區域。為減小誤差，可進一步采用以下的方法對判決結果做消除誤檢像素點的處理[6]：

設（x，y）為二值圖B中非零的像素點，在以它為圓心、半徑為R的區域D內，如果模糊點個數滿足式子（11），則B（x，y）=1；反之，B（x，y）=0.

其中，H為區域D中的像素點總數，T2為預設的閥值。

局部模糊區域檢測的具體算法如下：

（1）根據1.2節的算法計算整副圖像f（x，y）的頻域對數相關性系數Corr（x，y）.

（2）算出使得自相關系數Corr（x，y）滿足1.2節閥值條件的所有像素點（j，k）（對于其它不滿足閥值條件的像素點（j′，k′），都認為（j′，k′）∈R2，即B（j′，k′）=0）.

（3）對于（2）中的像素（j，k），根據1.3節的算法進一步計算其模糊測度q（j，k），若q（j，k）＜T1，則點（j，k）∈R1，B（j，k）=1；否則（j，k）∈R2，B（j，k）=0.

（4）消除二值圖B中的誤檢像素。

通過上述的局部模糊檢測算法，可以得到一副刀片前平面用黑色顯示，背景用白色顯示的二值圖，刀片周邊刃的邊緣即為這幅二值圖中黑色區域和白色區域的交界線。

2 雙樹復小波

2.1 DWT及其缺陷

DWT，即離散小波變換，是時頻分析一個非常強大的工具。由于其采用多分辨率的方法，通過伸縮和平移運算對信號進行多尺度細化，能自動適應時頻信號分析的要求，故可以聚焦到信號的任何細節，因而被稱為“數學顯微鏡”[7]。然而，它本身存在的一些缺陷卻大大限制了其在實際工程中的應用：

（1）不具有平移不變性。這將造成只要信號平移一段微小的距離，各尺度上小波系數的能量分布就會發生較大的變化。

（2）缺乏方向選擇性。傳統的離散小波變換方向分辨率較低，小波變換系數只能表示三個空間方向的信息，即水平、垂直和對角線三個方向。

（3）會產生Gibbs效應。由于分解和重構濾波器發生震蕩，故在圖像邊緣會有偽輪廓的產生，主要表現為震鈴和鋸齒。

2.2 雙樹復小波變換（DTCWT）

為了克服DWT所存在的種種缺陷，Kingsbury[8]于1999年提出了雙樹復小波變換（Dual-tree Complex Wavelet Transform，DTCWT）。它除了保持傳統小波變換多分辨率特性和較好的時頻局部化分析能力外，還具有以下優點：

（1）近似的平移不變性。信號的平移基本不會使各尺度上小波系數的能量分布發生變化。

（2）良好的方向選擇性。它能提供6個空間方向的信息，故能更好的描述圖像的方向屬性。

（3）有限的數據冗余。

（4）完全重構性。使用短的線性相位的濾波器組就可以實現完全重構。

雙樹復小波變換（DTCWT）采用兩棵離散小波樹的結構形式，一棵代表變換后的實部，另外一棵代表變換后的虛部，通過這兩棵樹并行實現實部和虛部的運算，如圖2所示。

圖2 二維雙樹復小波變換的分解

從圖2可知，將每一級分解后除可以得到兩個低頻分量A（j+1，1）和A（j+1，2）外，還可以得到6個不同的高頻分量D（j+1，m），m=1，...，6，同時無論二維雙樹復數小波變換分解樹有多深，其總體數據冗余都為4∶1，故這6個處于同一分解層的高頻分量對應了圖像中6個不同方向的信息（±15°，±45°，±75°）。由于其比DWT變換多了3個方向，因此雙樹復小波變換可顯著提高圖像分解與重構的精度并能更好的保留圖像的細節信息，如邊緣等。

3 實驗結果與分析

驗證實驗平臺如圖3示，垂直位移升降臺由伺服電機驅動系統控制進行對焦位置的判定和視野的吊證，環形燈用于對被測件進行打光操作，背光板用于進行高對比度影像的獲取。

圖3 實驗系統

實驗中，首先把待檢測的刀片放到背光板上以供拍照，然后對鏡頭調焦，使得刀片前刀面在圖片上所呈現的像清晰，而其他背景信息所呈現的像模糊，具體拍攝出的圖片如圖4所示。接著對圖片進行圖像處理以檢測刀片的邊緣。這其中計算像素相關性系數的四領域尺寸為N=5，計算新型判別算子的窗口尺寸為K=3.根據文獻[1]中的大量實驗統計可知，大部分模糊像素的相關性系數集中在（0.8，0.95）之間。因此本文也選取該相關性系數范圍進行模糊像素的搜尋，當同時滿足q

圖4 實驗所拍下的原始圖片

圖5 局部模糊檢測后的圖片

圖6雙樹復小波變換后的圖片

圖6 所示為應用本文所提方法而進行的刀片的緣輪廓曲面，如圖所示，該方法能夠準確地檢驗出刀片的邊緣輪廓曲線，與傳統方法對比可得該方法能夠同時對影像視野內的多個刀片同時進行尺寸校驗和加工檢測。較之常用的Robert算子和Sobel算子該方法更能夠有效地避免多點邊緣輪廓等問題。

綜上所述，本文所述方法能夠快速準確檢測出多個可轉位刀片周邊刃的邊緣輪廓信息，且刀片周邊刃邊緣清晰具體，為之后的尺寸檢測和刀片加工質量的檢驗提供了一個良好的基礎。

4 結束語

本文針對目前可轉位刀片邊緣檢測方法只能檢測一塊刀片的不足，提出了一種適用于多個可轉位刀片的邊緣檢測算法。該算法主要分為局部模糊檢測和雙樹復小波變換兩部分：先用局部模糊檢測把事先拍好的圖片（刀片前刀面區域清晰、背景區域模糊）作模糊檢測并生成二值圖（刀片前刀面顯示為黑色、背景區域顯示為白色），緊接著再對二值圖作雙樹復小波變換后就可以馬上檢測到多個可轉位刀片的邊緣（用黑色條紋表示）。實驗結果表明，用這個方法可以準確可靠地檢測出多個可轉位刀片周邊刃的邊緣，且沒有發生誤判的情況。

[1]朱德華.接觸式測量技術和非接觸式測量技術的融合[J].技術與市場，2012，19（5）:171-171.

[2]羅琪.可轉位刀片磨削誤差測量及其補償技術[D].廈門：廈門大學，2016.

[3]尚雅層，陳靜，田軍委.亞像素邊緣檢測算法在刀具參數檢測中的應用[J].計算機工程與科學，2011，33（4）:107-109.

[4]Marr D，Hildreth E.Theory of edge detection[J].Proceedings of the Royal Society of London B:Biological Sciences，1980，207（1167）:187-217.

[5]曾俊.圖像邊緣檢測技術及其應用研究[D].武漢：華中科技大學，2011.

[6]王睿，方勇.一種圖像局部模糊檢測方法及其在被動圖像認證中的應用[J].高技術通訊，2009，19（7）:718-723.

[7]王婷君.基于雙樹復小波和NPSO的醫學圖像配準方法研究[D].沈陽：東北大學，2009.

[8]Kingsbury N.Complex wavelets for shift invariant analysis and filtering of signals[J].Applied and computational harmonic analysis，2001，10（3）:234-253.

A PeripheralEdge Detection Method forMultiple Indexable Inserts

CHEN Yu-tong1，YE Jun-jun1，CHEN Bin-qiang1，SUNWei-fang1，LILing-xiang2
（1.School of Aerospace Engineering，Xiamen University，Xiamen Fujian 361005，China；2.Xiamen Golden Egret Special Alloy Co.，Ltd.，Xiamen Fujian 361000，China）

As for the problem of peripheral edge detection for indexable inserts，this paper propose an algorithm of edge detection based on local-blur detection and dual-tree complex wavelet transform formultiple indexable inserts.The algorithm have two steps:the first step is to take pictures of indexable inserts according to the requirements specified in advance firstly，and then make local-blur detection in the picture which was been taken，here the algorithm of edge detection judge whether the pixel is in the blur area with the correlation coefficients of the pixel in the picture and the new operator based on laplacian operator as evaluation indexs（if it is in the blur area，show it in white；otherwise，show it in black）.After eliminating the mistake pixels，the last step of the algorithm of edge detection will create a binary image，the peripheral edge of indexable inserts are the demarcation lines between white areas and black areas in the binary image.The second step is to detect the edges in binary image by using dual-tree complex wavelet transform，the result ater transform is that we need.Experimental results show that thismethod can detect the peripheral edge ofmultiple indexable inserts quickly and accurately.

indexable inserts；peripheral edge；edge detection；local-blur detection；dual-tree complex wavelet transform

TH741

A

1672-545X（2017）04-0158-05

2017-01-16

閩發改投資[2016]482號

陳宇彤（1990－），男，福建泉州人，碩士研究生，主要研究方向為機器視覺、機械磨損及圖像處理；葉軍君（1962－），男，福建莆田人，博士，副教授，主要從事CAD/CAM技術及協同設計技術方面的研究；陳彬強（1986－），男，福建廈門人，博士，助理教授，研究方向為復雜曲面加工制造、結構健康監測；孫維方（1988－），男，湖北襄陽人，博士研究生，主要研究方向為復雜曲面成形及測量、圖像處理；李凌祥（1970－），男，福建安溪人，碩士，教授級高工，研究方向為精密制造。