含參函數的零點問題的處理策略

東北育才雙語學校　馬江寧

函數是每年高考數學中的必考問題.“含有參數的零點問題”涉及等式的分拆與變形、函數圖像和性質的探究，往往要求考生利用多種手段對函數的圖像、性質進行研究，并且問題的解決往往涵蓋函數與方程、數形結合、分類討論、轉化與化歸等四種數學思想，因此備受命題人的青睞，成為近年高考數學中的熱點問題.

含參函數的零點問題的特點是參數的不同取值對函數的零點產生影響.從題目形式上看分為兩種：一是可分離參數的函數，二是不可分離參數的函數，而后者往往以復合函數的形式出現.下面我們對這兩類問題舉例研究.

一、可分離參數的函數零點問題的處理策略

例1函數f（x）=x2-ax+1在區間上有零點，則實數a的取值范圍是____.

【解析】題意等價于方程x2-ax+1=0，在區間內有解，又x=0不是方程的解，

則f（x）=x2-ax+1的零點問題等價于y=a與y=的交點個數問題，

其圖像如下圖所示：

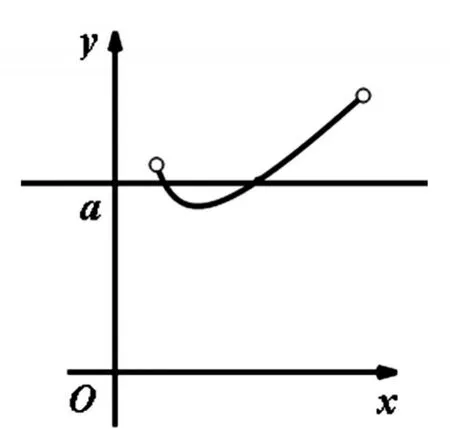
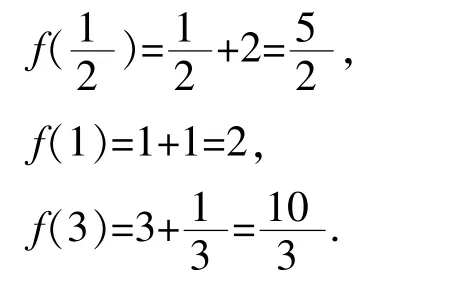
【總結提升】可以分離參數的函數的零點問題往往是：已知函數零點個數，求參數取值范圍.解決這類問題，我們可以先把所求變量進行分離，然后畫出分離變量后的函數圖像 （函數確定，圖像固定——靜），最后通過平移直線（參數變化，直線平動——動），采用動靜結合的方式，形象直觀地找符合題意的交點情況進行解答.

同時要學會辯證地處理問題，比如有些題目分離出簡單的含參函數更為簡潔，接下來只需要考查該函數隨著參數的變化規律即可，看下面的例子.

例2已……