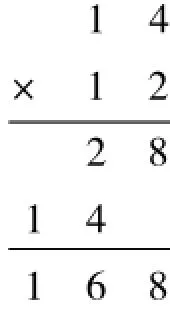“除數是小數的除法”教學研究報告

文︳長沙市岳麓區博才咸嘉學校數學組瀟湘數學教育工作室

“除數是小數的除法”教學研究報告

文︳長沙市岳麓區博才咸嘉學校數學組瀟湘數學教育工作室

一、問題

小數除法計算是人教版數學教材五年級上冊中的一個內容，這個內容分兩個部分：除數是整數的除法和除數是小數的除法。除數是小數的除法是本單元的學習重點，其關鍵是把除數是小數的除法轉化成除數是整數的除法。學生由于在這之前計算的都是除數是整數的除法以及受其他一些因素的影響，在計算除數是小數的除法時，盡管老師反復講解，也多次進行練習，還是經常出錯。一線數學教師普遍反映這個內容難教、學生難學。我校數學組在這個內容的教學上進行了嘗試與思考，力圖在計算正確率上有所突破。

1.教學實踐中的問題及原因分析

為了更加清楚地掌握學生出錯的原因，我們對學過的50名學生做了一個調查。題目如圖1所示。通過調查，我們發現學生主要存在以下五個問題。

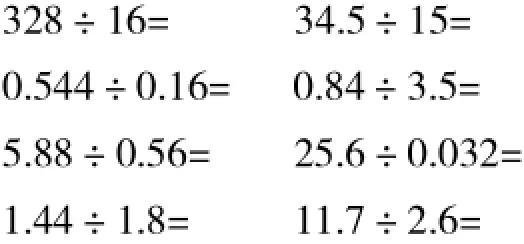
圖1

（1）學生計算時把除數當作整數，而被除數則不變（如圖2所示）。

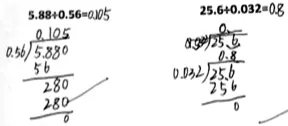
圖2

學生以前學習的都是除數是整數的除法，受定式思維的影響，在遇到除數是小數的除法時，習慣將它按照除數是整數的除法進行計算。之所以會出現這樣的錯誤，是學生沒有進一步思考：除數擴大變成整數后，如果被除數不跟著擴大相同的倍數，商的大小就改變了。

（2）學生不知道怎樣轉化。

學生計算5.88÷0.56時，會把被除數、除數同時擴大100倍，變成588÷56，而在計算0.544÷ 0.16時，卻把被除數0.544擴大1000倍變成544，除數0.16擴大100倍變成16。可以看出，學生知道計算時要把除數轉化為整數，但沒有根據商不變的性質把被除數和除數同時擴大相同的倍數。

（3）學生忘記打小數點（如圖3所示）。

（4）當被除數不夠除時，學生沒有在商中間相應的位置添0占位（如圖4所示）。

圖3

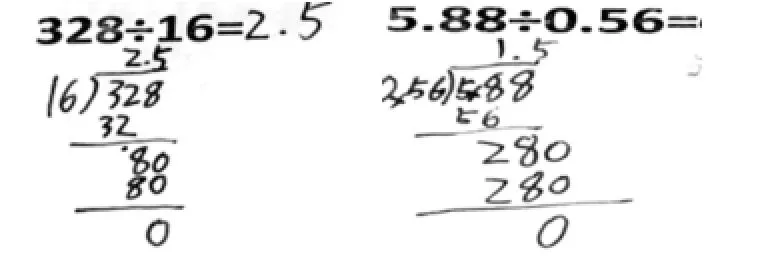
圖4

（5）學生試商不熟練。

進一步分析這5種錯誤，我們發現：第1、2種錯誤的原因是學生沒有掌握知識的關鍵點——怎樣將除數是小數轉化成除數是整數；第3、4、5種錯誤的原因是學生對以前所學的與此知識相關的基礎知識掌握得不牢固。

2.教學對策

通過對學生出錯原因的分析，我們認為在教學這個內容時，應將重點放在幫助學生解決如何將除數是小數轉化成除數是整數上。

（1）引導學生自主分析出錯的原因。

由于除數是小數的除法是在除數是整數的除法基礎上進行學習的，在教學除數是小數的除法時，教師一般會讓學生先嘗試做一做。一些基礎知識掌握得不扎實的學生難免會出錯。教師可以趁機引導學生分析錯誤的原因，讓他們知道自己錯在哪里，應該怎樣改正。比如，有學生在嘗試計算7.65÷0.85時出錯了，在匯報時，教師除了講解如何正確計算外，還應該跟其他學生一起，傾聽出錯的學生是怎樣想的，幫助他分析原因，糾正錯誤，避免下次再錯。

（2）針對知識的關鍵點進行轉化的專項練習。

除數是小數的除法是老師們公認的計算教學中的一大難點。為什么學生老是出錯呢？通過測試、分析、研討，我們發現：其實除數是小數的除法與除數是整數的除法在計算方法上是一致的，關鍵是學生需要根據商不變的性質把除數由小數轉化成整數再進行計算。學生容易出錯是因為不會進行轉化。再反觀我們的課堂，教師在課堂上很少甚至是沒有針對除數和被除數小數位數的不同情況，讓學生進行專門的轉化練習，沒有很好地突破難點，學生出錯也就在所難免。基于此，我們覺得在探究新知環節后要針對這個關鍵點，專門設計轉化的練習。如，先出示一組包含各種情況的除數是小數的計算題，要求：不計算，直接把它們轉化成除數是整數的除法。接著引導學生觀察轉化后的除數，發現擴大10倍、100倍、1000倍，就是把小數點向右移動一位、兩位、三位。緊跟著出示一組包含各種情況的除數是小數的計算題，要求學生直接移動小數點，把它們轉化成除數是整數的除法算式。這樣放慢節奏、放緩坡度，把重點放在把除數由小數轉化成整數上。

二、實踐

1.幫助學生辨析計算錯誤的原因。

師：現在，你想挑戰一下，計算出7.65÷0.85的得數嗎？給你4分鐘時間，開始。

師巡視，指名做完的學生板演（如圖5所示）。

師：算出的結果等于9，你是怎樣算出來的？

生1：把除數的小數點向右移動2位，化成整數，然后把被除數的小數點也向右移動2位。這樣都變成整數，就是整數除以整數啦。

師：我們一起看看他是怎樣變成整數除法的（邊說邊用手指豎式）。除數0.85變成85，擴大100倍。被除數7.65變成765，擴大100倍。也就是除數和被除數同時擴大100倍，商不變，這是我們學過的商不變性質。有個同學是這樣算的（如圖6所示），你們覺得他這樣做是怎樣想的？

生2：他是把0.85擴大100倍，而7.65不變，商就是原來的百分之一。

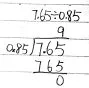
圖5

圖6

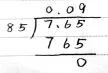
圖7

師：他的意思是：被除數沒變，還是7.65，除數變成85。（在旁邊板書豎式，如圖7所示）原來7.65÷85的結果才是0.09，出現這個結果是他把除數當作85計算的。如果除數擴大100倍，但被除數不變，商就是原來的百分之一，如果還原就要擴大100倍。7.65÷0.85正確的結果是9。現在我們回過頭看看：7.65÷0.85，除數是小數的除法我們是怎樣算出結果的？

生3：把它轉化成除數是整數的除法。

生4：把除數和被除數同時擴大相同的倍數再計算。

師追問：擴大相同倍數的目的是什么？

生5：使除數變成整數，商的大小也不變，就是我們學過的知識了。

設計意圖：設計辨析錯誤的環節，幫助學生分析并弄清錯誤的原因，加深印象，避免再出錯。

2.專門設計轉化的環節，幫助學生突破難點。

師：把下面的算式轉化成除數是整數的除法算式。說說你是怎樣將除數轉化成整數的。

2.38÷0.340.544÷0.165.2÷0.32

生6：2.38÷0.34，先把被除數2.38擴大100倍，變成238；（生說，師畫箭頭）再把除數0.34擴大100倍，變成34。（師完善板書）

師總結：把被除數2.38擴大100倍，變成238；再把除數0.34擴大100倍，變成34。那0.544÷0.16呢？

生7：先把0.544乘1000，變成544；再把0.16乘1000，變成160。（板書）

師：你這樣做的依據是什么？

生7：因為0.544已經乘了1000，要使商不變，0.16也要乘1000。

師：也就是要同時乘1000。現在變成了544÷ 160。還有同學舉手，你來說。

生8：把0.544乘100，變成54.4；然后0.16也乘100，變成16。這樣就變成了學過的除數是整數的除法。

師：看來乘100也可以啊。既然乘100就可以了，何必乘1000呢？只要把除數變成整數就可以了，被除數是不是整數我們都會計算了。所以計算除數是小數的除法時，我們一般是以除數為準，先把除數變成整數，再將被除數擴大相同的倍數，然后進行計算。

設計意圖：利用把0.544÷0.16轉化成除數是整數這一題，引導學生思考、比較，讓學生體會把它轉化成54.4÷16比轉化成544÷160要更合理、簡潔，進而發現計算小數除法時，是根據除數的小數位數進行轉化。

師：接下來我們看5.2÷0.32。誰來說說你是怎么計算的？

生9：把除數0.32擴大100倍變成32，再把被除數5.2擴大100倍，變成520。

師追問：為什么擴大100倍？

生9：這樣的話除數就變成整數了。

師：我們把這3個算式轉化成了除數是整數的除法，仔細觀察，我們是怎樣把它們轉化成除數是整數的除法的？

生10：將被除數與除數同時擴大100倍。

師：都是擴大100倍，那小數點如何移動呢？

生11：向右移動2位。

師：擴大100倍，其實就是把小數點向右移動2位。下次擴大100倍時，就不用乘100，直接把小數點向右移動2位。擴大10倍時，就直接把小數點向右移動1位；擴大1000倍時，就直接把小數點向右移動3位。現在，我們可以直接移動小數點的位置，把除數是小數的除法轉化成除數是整數的除法。請大家直接移動小數點的位置，把這些算式轉化成除數是整數的除法。

5.58÷3.17.05÷0.470.756÷0.18

51.3÷0.2725.6÷0.3226÷0.13

生12：5.58÷3.1，把3.1的小數點向右移動1位，把5.58的小數點也向右移動1位，變成55.8÷ 31。（生說，師移動小數點）

師：現在請在練習紙上將剩下的幾題移動小數點的位置，把它們轉化成除數是整數的除法。2分鐘時間，看誰做得又快又對。

學生動手練習。

師：老師走了一圈，發現大家做得很好，我們重點看看第二排的幾道題。51.3÷0.27，誰來說說你是怎么做的？

生13：將0.27的小數點向右移動2位，51.3的小數點向右移動2位，變成5130÷27。

師追問：51.3怎樣移動小數點變成5130？

生13：將51.3的小數點向右移動1位，變成513；再向右移動1位，添0，變成5130。（生說，師用手勢展示移動的過程）

師：那26÷0.13呢？

生14：先把除數0.13的小數點向右移動2位，再把被除數26的小數點也向右移動2位，添1個0，再添1個0。（生說，師用手勢展示移動的過程）

師：被除數位數不夠就在末尾補0，26÷0.13就變成了2600÷13。

設計意圖：針對小數除法計算過程中最關鍵的步驟精心設計，旨在分散知識的難點，提高學生計算的正確率。

三、思考

1.課前鞏固整數除法的計算，為除數是小數的除法掃清障礙。

回顧學生學習除數是小數的除法的過程，我們發現很多學生由于對除數是整數的除法計算不熟練，導致在除數是小數的除法計算中出現各種錯誤，如：計算時商的中間有0，沒有在商的相應位置添0占位；試商不熟練，等等。同時，老師們發現小數除法之所以難教、難學，一個重要原因是，即便學生正確地將小數除法轉化成整數除法后，很多學生還是不會做。而出現這種情況是因為學生在計算除數是兩位數的除法時不會試商。因此，計算教學中，在開展新內容的教學之前，根據需要可以增加一節預備課，用于復習、鞏固新知識學習的必備基礎。比如，學習除數是小數的除法之前，花一節課時間復習除數是兩位數的整數除法；學習除數是兩位數的除法之前，花一節課時間復習除數是一位數的除法；學習兩位數乘三位數的乘法之前，花一節課時間復習一位數乘多位數的乘法。所謂“磨刀不誤砍柴工”。我校數學組一直堅持每天做“計算三分鐘”練習，五年級學生在學習除數是小數的除法之前就可以利用這個計算練習時間有針對性地練習整數除法中學生的知識薄弱處和容易出錯的地方，為除數是小數的除法學習掃清障礙。

2.暫時講不清道理時不妨直接告訴學生。

在數學課堂上，我們經常會碰到這樣一種情況：有的知識點試圖和學生說道理時，發現目前難以找到簡單有效的方法讓學生明白。如果繼續說下去，不僅耽誤了課堂寶貴的時間，效果還不好。這時老師該如何取舍呢？我們是否可以換種思路，當道理說不清楚時不妨直接告訴學生呢？本節課學習的除數是小數的除法，在計算時要將算式轉化成除數是整數的除法，為什么是以除法為準而不是以被除數為準呢？處理這個問題時，我們發現很難找到一個突破口，也無法跟學生說清楚。再三思考后教師做了這樣的處理：沒有在計算7.65÷0.85時就直接告訴學生把它轉化成剛學過的除數是整數的除法來計算，而是放在練習環節進行處理。在將0.544÷0.16轉化成除數是整數的除法算式時，學生出現了兩種答案544÷160和54.4÷16，教師順勢引導學生對兩種答案進行對比，從而發現：其實轉化成54.4÷16我們就會計算了。這時教師告訴學生在計算除數是小數的除法時，只要把除數變成整數就可以了，被除數是不是整數我們都會計算了。因此在計算除數是小數的除法時，我們一般是以除數為準，先把除數化為整數，再將被除數擴大相同的倍數。

在計算教學中，與這種情況類似的還有三年級下冊兩位數乘兩位數這一內容。以14×12為例，用豎式計算如右圖所示。豎式這樣寫時，我們一般先用第二個因數12中個位上的2乘14，再用十位上的1乘14。為什么不先用第一個因數14中個位上的4乘12，再用十位上的1乘12呢？雖然我們都是把其中一個因數拆成幾十加幾，再分別用個位上的幾乘另一個因數和十位上的幾乘另一個因數，但用豎式計算時我們一般就是把第二個因數拆成幾十加幾再計算，而不拆第一個因數。教學時也很難和學生說清楚道理，我們同樣也可以選擇直接告訴學生。

計算能力對學生而言是很重要的一項技能，能為學生以后的學習提供必要的基礎。在日常教學中，我們老師一定要持之以恒，想方設法提高學生的計算能力，從而讓計算教學更高效。

（執筆：姚鑫、陳艷萍、謝凌燕、陳安、賀迎舟、鄭志剛、徐旺、李闖）