例談參數(shù)的分離技巧

文︳曾益俊

例談參數(shù)的分離技巧

文︳曾益俊

求參數(shù)的取值范圍問(wèn)題是中學(xué)數(shù)學(xué)中常見(jiàn)的問(wèn)題，既是教學(xué)重點(diǎn)、難點(diǎn)，也是高考的熱點(diǎn)。筆者在教學(xué)實(shí)踐中發(fā)現(xiàn)，把參數(shù)從方程或不等式中分離出來(lái)，使問(wèn)題轉(zhuǎn)化為求函數(shù)最值或值域問(wèn)題，或者將方程或不等式中的未知變量與參數(shù)進(jìn)行換位思考，把問(wèn)題看成以參數(shù)為未知變量的方程或不等式，能夠使問(wèn)題簡(jiǎn)單。

一、求方程中參數(shù)的取值范圍

例1已知關(guān)于x的方程4x+a2x+a+1=0有實(shí)根，求實(shí)數(shù)a的取值范圍。

分析：方程可化為：（2x）2+a2x+a+1=0，轉(zhuǎn)化為關(guān)于2x的二次方程，則方程的判別式駐逸0，以及有正實(shí)數(shù)根，從而建立不等式組求解。觀察題目中的參數(shù)a是一次，則嘗試將a分離出來(lái)，變?yōu)閒（a）形式，也許會(huì)更好。

所以f（x）的值域?yàn)椋?肄，2-22姨］，故a的取值范圍是

例2a取何值時(shí)，方程lg（x-1）+lg（3-x）=lg（ax）有一解，兩解，無(wú)解？

分析：原方程可化為：x2-5x+a+3=0（1＜x＜3），然后根據(jù)一元二次方程討論何時(shí)有一解，兩解，無(wú)解。這樣的話，必會(huì)帶來(lái)比較繁雜的解答。由于參數(shù)a是一次，則可仿照例1的方式，分離參數(shù)a試試。

解：原方程可轉(zhuǎn)化為：（x-1）（3-x）=a-x（1＜ x＜3），分離參數(shù)，得

4

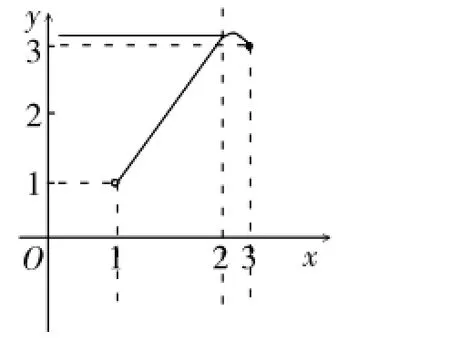
二、求不等式中參數(shù)的取值范圍

分析：對(duì)x，y取一些值試試，看能否得出a取值的大致范圍。

例4如果x∈［0，-肄），不等式x2+（p-1）x+1逸0恒成立，求實(shí)數(shù)p的取值范圍。

分析：運(yùn)用二次函數(shù)f（x）=x2+（p-1）x+1思考的話，對(duì)x＜0時(shí)如何剔除？一時(shí)難有好的辦法，換個(gè)角度思考，分離出參數(shù)p試試。

解：原不等式可化為：xp逸-x2+x-1。

（1）當(dāng)x=0時(shí)，0逸-1恒成立；

由（1）（2）可知：p逸-1。

三、求不等式中參數(shù)的取值范圍

例5對(duì)于滿足0≤p≤4的所有實(shí)數(shù)p，不等式x2+px＞4x+p-3恒成立，求x的取值范圍。

分析：已知p∈［0，4］，如果能夠建立一個(gè)關(guān)于p為變量的一次函數(shù)關(guān)系式，則容易解決。

解：把本題的不等式看作關(guān)于p的不等式進(jìn)行變量轉(zhuǎn)換，則問(wèn)題轉(zhuǎn)化為關(guān)于p的不等式：（x-1）p+ x2-4x+3＞0在0≤p≤4時(shí)恒成立。

令f（p）=（x-1）p+x2-4x+3，則

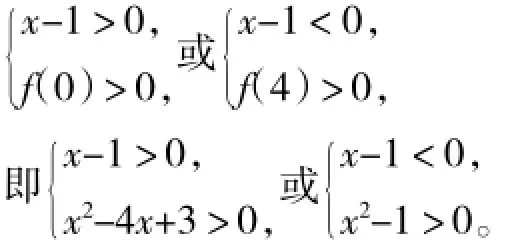
解得：x＞3或x＜-1。

故實(shí)數(shù)x的取值范圍是{x|x＜-1或x＞3}。

綜上所述，當(dāng)參數(shù)的指數(shù)是一次時(shí)，參數(shù)的分離與轉(zhuǎn)換是求解不等式或方程中參數(shù)取值范圍的好方法。它不僅運(yùn)算簡(jiǎn)潔，思路清晰，而且對(duì)所討論的問(wèn)題結(jié)構(gòu)明明白白，解題的關(guān)鍵是分離出參數(shù)之后將原問(wèn)題轉(zhuǎn)化為求函數(shù)的最值或值域問(wèn)題。這樣處理，能加深學(xué)生對(duì)方程、不等式、函數(shù)之間的關(guān)系的理解，也能培養(yǎng)學(xué)生的創(chuàng)造性思維能力。

（作者單位：邵東縣三中）